К решению номера 6 контрольной работы номер 1 .

 

1. а) Прямая линия как пересечение плоскостей.

Прямую линию в пространстве будем рассматривать как пересечение двух плоскостей. Обозначим через  и  какие-нибудь две различные плоскости, пересекающиеся по прямой . Уравнение  и известны:

Так как прямая 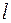  представляет собой пересечение плоскостей  и , то она определяется совместным заданием двух уравнений:

.

Б) Каноническое уравнение прямой.

Пусть дана какая-нибудь прямая. Каждый не равный нулю вектор, лежащий на этой прямой или параллельный ей, называется направляющим вектором этой прямой. Будем его обозначать .

Выведем уравнение прямой, проходящей через данную точку 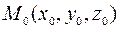 и имеющей данный направляющий вектор .

Пусть  - произвольная точка прямой. Вектор  коллинеарен направляющему , следовательно, справедливы формулы:

                           (2)

Уравнение (2) называется каноническим уравнением прямой.

Пример. Найти каноническое уравнение прямой

Решение. Легко убедится, что точка  принадлежит данной прямой. Нормали к указанным плоскостям имеют вид: , .

Отсюда ,

Следовательно,  и каноническое уравнение прямой имеет вид: .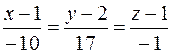

Задача. Составить каноническое уравнение прямой, проходящей через две данные точки:  и 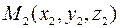 (самостоятельно).

В) Параметрические уравнения прямой.

Пусть дано каноническое уравнение прямой. Обозначим буквой   каждое из равных соотношений, которые учувствуют в этом уравнении.

,

Тогда 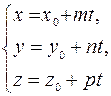  (3)

(3) – параметрическое уравнение прямой, проходящей через точку 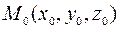 в направлении вектора . Здесь  рассматривается как произвольно изменяющийся параметр,  - как функции от .

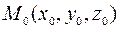Если параметру  придать значение времени, то уравнение (3) определяют прямолинейное и равномерное движение точки  со скоростью  в направлении вектора ; точка  - начальное положение точки .

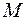1. Взаимное расположение двух прямых в пространстве.

 Две прямые в пространстве могут быть параллельны, совпадать, скрещиваться, пересекаться.

Пусть две прямые  и  заданы уравнениями:

                 

 

А) Условие параллельности прямых  и  заключается в коллинеарности их направляющих векторов, т.е.

              (4)

Б) Для совпадения прямых  и  кроме условия (4) необходимо и достаточно еще и условие

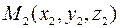, означающее требование, чтобы точка  лежала на прямой  (или чтобы точка  лежала на прямой ).

В) Если прямые  и  пересекаются, то они лежат в одной плоскости, следовательно, в одной плоскости должны лежать векторы: , , .

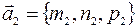Условие компланарности этих векторов имеет вид: (5)

             
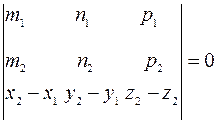
(5) – необходимое и достаточное условие пересечения двух прямых  и  в пространстве.

Г) Если условие (5) не выполнено, то прямые  и  скрещиваются.

3. Взаимное расположение прямой и плоскости.

Пусть в  дана прямая

,

Где  - ее направляющий вектор, и плоскость 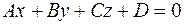, где  - нормаль к плоскости .

А) Если прямая  и плоскость  перпендикулярны, то , следовательно, .

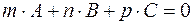Б) Если прямая  и плоскость параллельны, то , следовательно, .

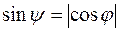В) Угол между прямой  и плоскостью , по определению, есть угол  между этой прямой и ее проекцией на плоскость . В зависимости от выбора направляющего вектора прямой и нормального вектора к плоскости  имеем всего четыре угла, образующие две пары вертикальных углов. Обозначим через  угол между любым направляющим вектором  и прямой  и любым вектором , нормальным к плоскости . Легко видеть, что . Угол   находится по формуле , значит .

 

 

Пример. Написать уравнение прямой, проходящей через точку 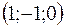 и перпендикулярной к плоскости .

Решение. , т.к. прямая перпендикулярна плоскости, то , следовательно,  - направляющий вектор прямой. Таким образом, искомое уравнение имеет вид:

.

4.Расстояние от точки до прямой.

Пусть дана точка  и прямой . Необходимо найти расстояние от точки  до прямой .

А) Найдем уравнение плоскости, проходящей через точку  и перпендикулярной прямой 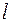. Т.к. ,  - нормаль к искомой плоскости, следовательно, можем написать уравнение:

 - искомое уравнение плоскости.

Б) Найдем точку пересечения этой плоскости с данной прямой. Для этого запишем уравнение прямой в параметрическом виде:

.

Чтобы найти точку пересечения прямой и плоскости, необходимо решить систему:

.

Решение – точка   - точка пересечения.

В) Искомое расстояние есть длина вектора 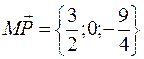. Следовательно,

ПРЯМАЯ НА ПЛОСКОСТИ

1. Прямая линия на плоскости определяется уравнением первой степени.

Уравнение  (1) с произвольными постоянными 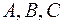, причем  и  не равны нулю одновременно, называются общим уравнением прямой на плоскости.

Пусть точка  лежит на прямой (1), тогда выполняется равенство:  (2).

Вычитая (2) из (1), получим .

Следовательно, векторы  и  ортогональны.

Таким образом, вектор с координатами  является нормалью к прямой (1).

Неполные уравнения прямой:

1)  - уравнение прямой, проходящей через начало координат;

2)  - прямая параллельна оси ;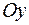

3)  - прямая параллельна оси ;

4)  - уравнение оси ;

5)  - уравнение оси .

2. Векторное и каноническое уравнение прямой.

Пусть дана какая-либо точка  и вектор , который считаем приложенным к точке 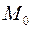: . Эти данные определяют прямую  как геометрическое место концов всевозможных векторов вида 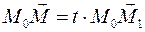. (3) , где  пробегает все вещественные числовые значения.

Вектор 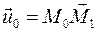 является направляющим вектором прямой (рис.1).

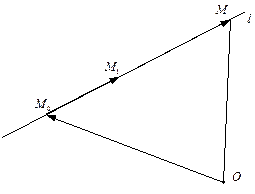
Если на плоскости раз навсегда дана точка  (начало координат), то уравнение (3) эквивалентно уравнению:          (4).

Это уравнение называют векторным уравнением прямой.

Пусть вектор  задан своими координатами , если при этом , , , то уравнение (4) эквивалентно системе двух уравнений:

Система уравнений (5) называется системой параметрических уравнений данной прямой или ее параметрическим уравнением;  - параметр.

Система уравнений (5) равносильна одной пропорции:

(6),

Которая называется каноническим уравнением прямой на плоскости.

Если прямая задана двумя своими точками  и , то ее направляющий вектор , имеет координаты: ;  и уравнение (6) представляется в виде         (7).

Это и есть уравнение прямой, проходящей через две заданные точки  и .

Если прямая не проходит через начало координат и не параллельна ни одной из координатных осей, то , , .

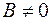 То уравнение (1) можно записать в виде

,      т.е. в виде 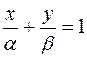    (8),

                                      где , .

Уравнение (8) называется уравнением прямой в отрезках.

Если прямая  дана своим общим уравнением (1), то для определения ее расстояния от точки  надо сначала привести уравнение прямой к нормальному виду, т.е. умножить обе его части на . В результате получим формулу: .

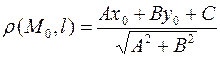1. Взаимное расположение прямых на плоскости.

Пусть на плоскости даны две прямые  и  соответствующими общими уравнениями:

.

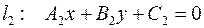Соответствующие векторы нормалей имеют координаты:

;                      .

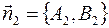Две прямые на плоскости могут быть параллельны друг другу, совпадать или пересекаться под произвольным углом.

А) Прямые 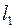 и  параллельны, следовательно, , т.е. .

Б) Прямые 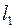 и  совпадают, следовательно, уравнения, их описывающие, эквивалентны, т.е. .

В) Прямые пересекаются под прямым углом, значит, . следовательно, .

Г) Прямые пересекаются под произвольным углом, тогда угол между прямыми равен углу между векторами  и , т.е. .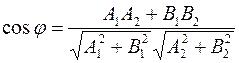

Пример. Показать, что прямые

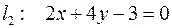 параллельны и найти расстояние между ними.

Решение. ; 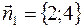, следовательно,  - прямые параллельны.

Точка 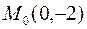 лежит на прямой , поэтому .

Дополнительные формулы:

1. Острый угол между  и

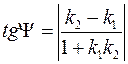
1. Условие параллельности

1. Условие перпендикулярности

1. Уравнение прямой, имеющей угловой коэффициент  и проходящей через точку

Уравнение пучка прямых

.

 

 

ПЛОСКОСТЬ В ПРОСТРПНСТВЕ

1. Всякая плоскость в пространстве, снабженном декартовой системой координат, есть множество вех точек, удовлетворяющих некоторому линейному уравнению вида:

             (1)

Обратно, множество всех точек 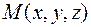,являющихся решениями произвольного уравнения (1), есть плоскость.

(1) – общее уравнение плоскости.

Пусть точка  лежит в плоскости (1), тогда выполняется равенство:   (2)

Вычтем (2) из (1):

 

Следовательно, векторы 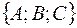 и  ортогональны. Таким образом, вектор 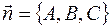 является нормалью к плоскости (1) и называется нормальным вектором плоскости.

Неполные уравнения плоскости:

А)  - уравнение плоскости, проходящей через начало координат;

Б) 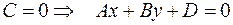 - уравнение плоскости, параллельной оси ;

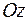В)  - уравнение плоскости, параллельной оси ;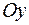

Г)  - уравнение плоскости, параллельной оси ;

Д)  - уравнение плоскости, параллельной координатной плоскости ;

Е)  - уравнение плоскости, параллельной координатной плоскости ;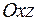

Ж) 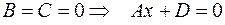 - уравнение плоскости, параллельной координатной плоскости .

 

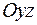1. Частные случаи уравнения плоскости.

Всякую плоскость в пространстве можно задать, указав какую – ни будь ее точку  и два произвольных приложенных к этой точке неколлинеарных вектора:

 и .

Прилагая векторы  и  к точке , получим всевозможные закрепленные векторы вида , где  - произвольные вещественные числа; концы 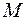 этих векторов и заполняют плоскость, проходящую через точку  и два приложенных к ней вектора .

В координатной форме уравнение (3) записывается так:

      (4)

(4) – параметрическое уравнение плоскости.

Уравнение (4) выражают линейную зависимость столбцов матрицы

Что эквивалентно равенству:

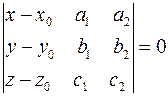      (5)

Пример. Найти уравнение плоскости, проходящей через три данные точки: ; ; .

Решение. Искомая плоскость содержит точку  и неколлинеарные векторы:

 и , следовательно, ее уравнение можно записать в виде (5):

Если все коэффициенты уравнения (1) отличны от нуля, тогда его можно записать в виде:

 

Или

               (6)

Где ; ; .

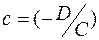(6) – уравнение плоскости в отрезках, т.к. числа 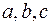 - алгебраические значения отрезков, отсеченных плоскостью (1) на осях координат.