Система упражнений учебника «Математика» 5-6 класс Зубарева И.И., Мордкович А.Г. по формированию умений составления математических моделей

 

Для рассмотрения этапов формирования умений перевода сюжета задачи на математический язык проанализируем учебник И.И. Зубаревой, А.Г. Мордковича «Математика, 5 класс».

1 этап. Составление и расшифровка числовых выражений.

§ 2. Числовые и буквенные выражения.

№32

Стоимость батона хлеба - 5р., а стоимость плитки шоколада – 15р. Запишите в виде выражения:

1) на сколько плитка шоколада дороже батона хлеба;

2) Во сколько раз плитка шоколада дороже батона хлеба;

3) стоимость плитки шоколада и батона хлеба вместе;

4) стоимость двух плиток шоколада;

5) стоимость трех батонов хлеба;

6) стоимость двух плиток шоколада и трех батонов хлеба вместе;

7) на сколько две плитки шоколада дороже трех батонов хлеба;

8) во сколько раз две плитки шоколада дороже трех батонов хлеба.

Найдите значения полученных выражений.

Начинаем разбор задачи с вопроса «Что нам известно в задаче?». Известно, что батон хлеба стоит 5 р., а плитка шоколада – 15 р. Мы должны записать выражения и найти их значения. Дети это делать умеют.

1) 15-5=на 10р. плитка шоколада дороже батона хлеба;

2) 15÷5=в 3 раза плитка шоколада дороже батона хлеба;

3) 15+5=20р. стоят батон хлеба и плитка шоколада вместе;

4) 15×2=30р.стоят две плитки шоколада;

5) 5×3=15р. стоят три батона хлеба;

6) 15×2+5×3=45р. стоят 2 плитка шоколада и 3 батона хлеба вместе;

7) 15×2-5×3=на 15р. две плитки шоколада дороже трех батонов хлеба;

8) (15×2)÷(5×3)= в 2 раза две плитки шоколада дороже трех батонов хлеба.

Мы ответили на все вопросы задачи. Нашли значения полученных выражений.

После этой задачи учащимся сообщается: все выражения, которые у вас получились, содержат только числа и знаки действий, такие выражения называются числовыми.

Дальше идет задача №33. Она другая, но при записи решения выясняется, что это то же самое, что и предыдущая задача, только в буквенном варианте.

2 этап. Составление и расшифровка буквенных выражений

№33.

Цена груш - р. за 1 кг, а цена моркови - р. за 1 кг. Запишите в виде выражения:

1) на сколько 1 кг груш дороже 1 кг моркови;

2) во сколько раз 1 кг груш дороже, чем 1 кг моркови;

3) стоимость 1 кг груш и 1 кг моркови вместе;

4) стоимость 2 кг груш;

5) стоимость 3 кг моркови;

6) стоимость 2 кг груш и 3 кг моркови вместе;

7) на сколько 2 кг груш дороже 3 кг моркови;

8) во сколько раз 2 кг груш дороже 3 кг моркови.

Чем отличаются эти выражения от тех, которые были получены в предыдущем задании? Как бы вы назвали эти выражения?

В задаче нам известно:

Цена 1 кг груш - р., цена 1 кг моркови - р.

Отличие этой задачи от предыдущей в том, что в задаче №32 были даны числовые значения. В этой задаче даны буквенные значения, получаются такие выражения:

 

 

Разбирается с детьми то, что эти выражения отличаются от выражений, полученных в предыдущем задании, тем, что они записываются с помощью букв и можно было бы их назвать буквенными.

Сразу после этой задачи идут выводы о том, что это действительно буквенные выражения. А также о том, что найти значения буквенных выражений можно, зная значения входящих в них букв.

Рассмотрим более сложное задание для 1-го этапа.

№39

Саша и Миша – братья. Саша любит ходить за грибами, а Миша ловить рыбу. Обычно, рано утром из дома они выходят одновременно, но идут в противоположных направлениях. Саша, собирая грибы, идет медленно, со скоростью 2 км/ч, а Миша торопится поскорее дойти до озера и идет быстро, со скоростью 6 км/ч.

Запишите выражения для следующих величин:

1) расстояние между грибником и рыболовом через час после начала движения;

2) скорость, с которой грибник и рыболов удаляются друг от друга;

3) расстояние между грибником и рыболовом через 2 ч после выхода;

4) расстояние, пройденное грибником за 2 ч;

5) расстояние, пройденное рыболовом за 2 ч;

6) на сколько расстояние, пройденное рыболовом за 2 ч, больше расстояния, пройденного за то же время грибником;

7) во сколько раз расстояние, пройденное рыболовом за 2 ч, больше расстояния, пройденного за то же время грибником.

Найдите значения полученных выражений.

Что нам известно?

Саша ходит за грибами, со скоростью 2 км/ч,

Миша ходит ловить рыбу со скоростью 6 км/ч.

1) 6×1-2×1=4 км расстояние между ребятами через 1 ч;

2) 6-2=4 км/ч скорость удаления;

3) 6×2-2×2=8 км расстояние меду ребятами через 2 ч;

4) 2×2=4 км прошел Саша за 2 ч;

5) 6×2=12 км прошел Миша за 2 ч;

6) 12-4= на 8 км расстояние, пройденное Мишей больше расстояния пройденного Сашей.

7) 12÷4= в 3 раза расстояние, пройденное Мишей больше расстояния пройденного Сашей.

Следующий №40 из 2 этапа.

Из одного гаража одновременно в противоположных направлениях выехали автомобиль и автобус. Скорость автомобиля -  км/ч, а автобуса -  км/ч, причем автомобиль едет быстрее, чем автобус.

Запишите в виде выражения:

1) расстояние между автомобилем и автобусом через час после начала движения;

2) скорость, с которой автомобиль и автобус удаляются друг от друга;

3) расстояние между автомобилем и автобусом через 2 ч после начала движения;

4) расстояние, которое прошел автомобиль за 2 ч;

5) расстояние, которое прошел автобус за 2 ч;

6) на сколько расстояние, пройденное автомобилем за 2 ч, больше расстояния, пройденного за то же время автобусом;

7) во сколько раз расстояние пройденное автомобилем за 2 ч, больше расстояния , пройденного за то же время автобусом.

Нам известно, что скорость автомобиля -  км/ч, а автобуса -  км/ч.

 

 

Сравнивая №39 и №40 понимаем, что выражения с 1 по 7 получились одинаковые, только в №39 числовые выражения, а в №40 буквенные выражения. И если заменить скорости Миши и Саши на буквенные обозначения  и , то выражения станут одинаковыми.

№49

Какое число больше, a или b, если:

 

а) b;

б)  a;

в) b;

г) a.

 

№50

Какое число больше, 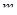 или , если:

 

а)  m

б)  m

в)  n

г)  n

 

№51

а) число m на 8 больше числа n: m-8=n;

б) число a в четыре раза больше числа b: 4×b=a;

в) число c на 3 меньше числа d: d-3=c;

г) число e в шесть раз меньше числа g: 6×e=g.

Постепенно ситуация усложняется.

№60. Движение навстречу (числовые выражения)

Из пунктов А и В, расстояние между которыми 260 км, одновременно навстречу друг другу выехали велосипедист и мотоциклист. Скорость велосипедиста – 13 км/ч, а мотоциклиста – 52 км/ч.

Запишите в виде выражения:

1) на сколько скорость велосипедиста меньше скорости мотоциклиста: 52-13= на 29 км/ч скорость велосипедиста меньше скорости мотоциклиста;

2) во сколько раз скорость велосипедиста меньше скорости мотоциклиста: 52÷13= в 4 раза скорость велосипедиста меньше скорости мотоциклиста;

3) время, которое потребуется велосипедисту на весь путь из А в В: 260÷13=20 часов потребуется велосипедисту на весь путь;

4) время, которое потребуется мотоциклисту на весь путь из А в В: 260÷52=5 часов потребуется на весь путь мотоциклисту;

5)на сколько меньше времени потребуется на весь путь мотоциклисту, чем велосипедисту: 20-5=на 15 часов меньше потребуется мотоциклисту, чем велосипедисту;

6)во сколько раз меньше времени потребуется на весь путь М., чем В.: 20÷5=в 4 раза меньше времени потребуется М., чем В.

7) скорость сближения В. и М.: 13+52=65 км/ч;

8) через какое время после начала движения В. и М. встретятся: 260÷(13+52)= через 4 ч.

№61. Движение навстречу (буквенные выражения).

Из пунктов А и В, расстояние между которыми 260 км, одновременно навстречу друг другу выехали автобус и автомобиль. Скорость автобуса – x км/ч, а скорость автомобиля – y км/ч . Запишите в виде выражения:

1) на сколько скорость автобуса меньше скорости автомобиля:

;

2) во сколько раз скорость автобуса меньше скорости автомобиля: ;

3) время, которое потребуется автобусу на весь путь из А в В: ;

4) время, которое потребуется автомобилю на весь путь из А в В: ;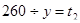

5) на сколько меньше потребуется времени на весь путь из А в В автомобилю, чем автобусу: ;

6) во сколько раз меньше потребуется времени на весь путь из А в В автомобилю, чем автобусу: ;

7) скорость сближения автобуса и автомобиля: ;

8) через какое время после начала движения автобус и автомобиль встретятся: .

Если сравнивать условия последних двух задач, то в них описаны похожие реальные ситуации на движение навстречу, только в первом случае выражения, которые мы составляли, были числовые, а во втором случае – буквенные.

№75. Движение вдогонку.

Вини-Пух был в гостях у Пятачка. Уходя, он забыл у него свой воздушный шарик. Пятачок заметил это только через 12 минут после ухода Вини-Пуха и сразу побежал за ним вдогонку, чтобы отдать шарик. Ему удалось догнать Вини-Пуха довольно быстро, поскольку тот шел не торопясь, со скоростью 50 м/мин, а Пятачок бежал быстро – со скоростью 200 м /мин.

Запишите на математическом языке:

1) какое расстояние Вини-Пух прошел за 12 минут: 50×12=600 метров;

2) на какое расстояние Пятачок приближался к Вини-Пуху за одну минуту: на 200 м;

3) сколько времени понадобилось Пятачку, чтобы догнать Вини-Пуха: 600÷200=3 минуты.

Следующая задача №76 такая же, только вместо числовых выражений составляются буквенные и вместо Винни-Пуха и Пятачка – волк с зайцем.

Задачи на движение по реке

№81

Скорость течения реки 2 км/ч, а собственная скорость катера 15 км/ч. Составьте выражения для следующих величин и найдите их значения:

1) скорость катера при движении по течению реки: 15+2=17 км/ч;

2) скорость катера при движении против течения реки: 15-2=13 км/ч;

3) расстояние, которое пройдет катер за 3 ч, двигаясь по течению реки: 17×3=51 км;

4) расстояние, которое пройдет катер за 3 ч, двигаясь против течения реки: 13×3=39 км;

5) время, которое потребуется катеру на путь 68 км при движении по течению реки: 68÷17=4 ч;

6) время, которое потребуется катеру на путь 78 км при движении против течения: 78÷13=6 ч;

7) на сколько скорость катера при движении по течению больше его скорости при движении против течения: 17-13=на 4 км/ч.

Полезно давать задания на составление буквенных и числовых выражений на геометрическом материале.

№92.

Длина отрезка АВ равна 50 см. Точки M и N лежат на этом отрезке. Найдите длину отрезка MN, если:

а) AM=15 см, NB=19 см, значит MN=50-15-19=16 см;

б) AN= 38 см, MB=26 см, значит MN=38+26-50=14 см;

в) AM=23 см, NB=21 см, значит MN=50-23-21=6 см;

г) AN=42 см, MB=34 см, значит MN=42+34-50=26 см.

№93.

Длина отрезка АВ равна  см. Запишите выражение для длины отрезка:

а) MN, который в 3 раза длиннее AB: MN=3 ;

б) KL, который на 25 см длиннее AB: KL= +25;

в) CD, который в 4 раза короче AB: CD= ÷4;

г) EF, который на 8 см короче AB: EF= -8.

№108.

Запишите выражение для длины ломаной ABCD, если:

а) AB=x, DC в 2 раза больше AB , а CD на 6 см меньше AB: AB=x, BC=2x, CD=x-6, тогда ABCD=x+2x+(x-6);

б) AB=y, BC в 3 раза меньше AB, а CD на 8 больше BC: AB=y, BC=y÷3, CD=y÷3+8, тогда ABCD=y+ y÷3+(y÷3+8).

Далее переходим к следующему 3 этапу расшифровке буквенных выражений в соответствии с данной ситуацией

№113

Книга стоит x р., а альбом – y р. Какой смысл имеет выражение:

а) 3x – стоимость трех книг;

б) 2y – стоимость двух альбомов;

в) y-x – разница между стоимостью альбома и стоимостью книги;

г) 5x+4y – стоимость пяти книг и четырех альбомов.

№114

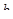Скорость пассажирского поезда -  км/ч, а товарного -  км/ч. Что записано на математическом языке:

а)  - скорость сближения пассажирского и товарного поездов;

б) 1750÷ - время, за которое пассажирский поезд пройдет расстояние в 1750 км;

в) 1750÷ - время, за которое товарный поезд пройдет расстояние в 1750 км;

г) 1750÷( ) – время, через которое два поезда встретятся.

§12. Формулы.

На этом этапе большое значение имеет введение понятия «формула», т.к. это тоже перевод в математический язык.

§13. Законы арифметических действий.

Словесная и буквенная формулировка законов сложения и умножения.

§16. Математический язык.

Математическая модель.

Второй и третий этапы не отделяются четко друг от друга, например, когда мы переходим к расшифровке выражения, это не значит, что мы перестаем составлять выражение.

После того как дети получили элементарное представление о составление выражений и их расшифровке целесообразно ввести такие понятия как математический язык и математическая модель, что авторы и делают.

№260

Переведите на обычный язык:

1) ;

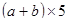2) ;

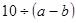3) ;

4) .

Проверьте себя

 

1) 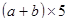;	произ-ние суммы чисел  и  и числа 5
2) ;	частное числа 10 и разности чисел  и
3) ;	сумма числа 5 и произ-ния чисел  и
4) .	разность утроенного числа  и числа

 

Обращается внимание на то, что чтение выражений начинается с последнего выполняемого действия.

№ 261

Переведите на обычный язык:

 

1) ;

2) ;

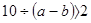3) ;

4) .

 

Проверьте себя.

 

1) ;	произведение суммы чисел  и  и числа 5 равно 15
2) 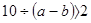;	частное числа 10 и разности чисел  и  больше двух
3) ;	сумма числа 5 и произведения чисел  и  меньше семи
4) .	разность утроенного числа  и числа  не равна трем

 

Следующие задания обратные двум предыдущим, теперь дана фраза, и надо записать ее на математическом языке.

№262

Запишите на математическом языке такие «слова»:

1) сумма первых четырех натуральных чисел;

2) произведение первых четырех натуральных чисел;

3) частное наибольшего двузначного и наибольшего однозначного чисел;

4) разность наименьшего трехзначного и наименьшего двузначного чисел,

В результате дети получают такие выражения:

1) ;

2) ;

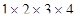3) ;

4) .

№263

Запишите на математическом языке предложения:

1) сумма первых четырех натуральных чисел равна десяти;

2) произведение первых четырех натуральных чисел равно двадцати четырем;

3) частное наибольшего двузначного и наибольшего однозначного чисел равно одиннадцати;

4) разность наименьшего трехзначного и наименьшего двузначного чисел равна девяноста.

В результате дети получают такие выражения

1) ;

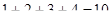2) ;

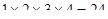3) ;

4) .

Следующее задание на составление выражения.

№264.

Цена хризантемы - р. за один цветок, а цена одной розы – на 30 р. больше. Запишите на математическом языке:

а) цену розы;

Если цена хризантемы - р, а цена розы на 30р. больше, тогда ответ цена розы – (30+ )р.

б) стоимости пяти хризантем;

Если цена одной хризантемы - р., то ответ цена пяти хризантем –5 р.

в) стоимости трех роз;

Если цена одной розы - (30+ )р., тогда ответ цена трех роз –3(30+ ) р.

г) стоимость букета из пяти хризантем и трех роз.

Если цена пяти хризантем - 5 р. и цена трех роз – (3(30+ ))р., то ответ букет из этих цветов будет стоить – (5 +3(30+ ))р.

Переходим к 4 этапу: составление равенств и неравенств.

№266.

Цена хризантемы -  р. за один цветок, а цена одной розы – на 30 р. больше. Запишите на математическом языке:

а) букет из пяти хризантем и трех роз стоит 250 р.: ответ ;

б) три розы дороже пяти хризантем на 50 р.: ответ ;

в) стоимость букета из семи хризантем меньше трехсот рублей: ответ ;

г) стоимость букета из семи роз больше трехсот рублей: ответ .

§17. Математическая модель

С целью дальнейшего формирования представлений о том, что с помощью одной и той же математической модели могут быть описаны различные с обыденной точки зрения ситуации, учащимся предлагаются следующие задачи.

№273.

Расстояние 180 км легковой автомобиль может преодолеть за 2 ч, а грузовому автомобилю на то же расстояние требуется 3 ч. Через какое время они смогут встретиться, если выедут навстречу друг другу из пунктов, расстояние между которыми 300 км?

Решение

180 км легковой автомобиль - за 2 ч, значит за 1 ч – 90 км. 180 км грузовой автомобиль – за 3 ч, значит за 1 ч – 60км.

300÷(90+60)= через 2 ч автомобили встретятся.

Ответ: через 2 часа.

№274

Одной бригаде трактористов, чтобы вспахать 180 а, требуется 2 дня, а другой – 3 дня. За какое время эти бригады смогут вспахать 300 а, работая одновременно?

Решение

300÷(180÷2+180÷3)=за 2 ч эти бригады могут вспахать 300 а.

Ответ: за 2 часа.

Для решения этих двух задач требуется найти значение одного и того же числового выражения: 300÷(180÷2+180÷3). Но это не является для учеников чем-то совершенно новым и необычным. Они уже сталкивались с тем, что на математическом языке различные с точки зрения обыденной жизни ситуации описываются совершенно одинаково.

В учебнике рассказывается о том, что полученное в процессе решения выражение – это математическая модель реальной жизненной ситуации, о которой говорится в задаче. В первой задаче рассматривается встречное движение, во второй – совместная работа, и обе эти ситуации описываются одинаковыми математическими моделями.

Ученики, выполняя задания из предыдущих пунктов по «переводу» обычной речи на математический язык каждый раз составляли математическую модель данной ситуации.

§27. Определение угла. Развернутый угол.

№509

Прочитайте задачу. Постарайтесь найти разные способы решения.

В двух коробках 16 кг печенья. Найдите массу печенья в каждой коробке, если в одной из них печенья на 4 кг больше, чем в другой.

Проверьте так ли вы решали задачу:

1 способ.

Если из первой коробки достать 4 кг печенья, то в обеих коробках печенья станет поровну, а всего останется 16-4=12 кг – печенья. Тогда в каждой коробке будет 12÷2=6 кг печенья. Но это как раз та масса печенья, которая была во второй коробке: 6+4=10 кг.

Ответ: масса печенья в первой коробке – 10 кг, а во второй – 6 кг.

2 способ.

Если во вторую коробку добавить 4 кг печенья, то в обеих коробках печенья станет поровну, а всего в двух коробках станет 16+4=20 кг печенья. Тогда в каждой коробке станет 20÷2=10 кг печенья. Но это как раз та масса печенья, которая была в первой коробке. Теперь можем узнать массу печенья во второй коробке: 10-4=6кг.

Ответ: масса печенья в первой коробке – 10 кг, а во второй – 6 кг.

3 способ.

Обозначим массу печенья во второй коробке буквой x кг.

Тогда масса печенья в первой коробке будет равна (x+4) кг, а масса печенья в двух коробках – ((x+4)+x) кг.

Но, по условию задачи, в двух коробках было 16 кг печенья. Значит, можем составить уравнение

(x+4)+x=16.

Решив его получаем x=6.

Итак, мы получили, что во второй коробке было 6 кг печенья, значит, в первой было 6+4=10 кг печенья.

Ответ: масса печенья в первой коробке – 10 кг, а во второй – 6 кг.

4 способ.

Обозначим массу печенья в первой коробке буквой x кг.

Тогда масса печенья во второй коробке будет равна (x-4) кг, а масса печенья в двух коробках – (x+(x-4)) кг.

По условию задачи, в двух коробках было 16 кг печенья. Составим уравнение

x+(x-4)=16.

Отсюда x=10.

Итак, мы получили, что в первой коробке было 10 кг печенья, значит, во второй было 10-4=6 кг печенья.

Ответ: масса печенья в первой коробке – 10 кг, а во второй – 6 кг.

3 и 4 способы решения задачи – это один и тот же способ: алгебраический. Решая задачу алгебраическим способом, обозначают неизвестную величину буквой, составляют уравнение по условию задачи и решают его.

№510.

С трех участков земли собрали 156 ц картофеля. С первого и второго участков картофеля собрали поровну, а с третьего – на ц больше, чем с каждого из первых двух. Сколько картофеля собрали с каждого участка?

 

1 поле
2 поле
3 поле		2 ц

 

Всего 156 ц

1 способ.

Если на двух первых полях количество собранного картофеля одинаковое, на третьем на 12 ц больше, то мы можем из общей суммы 156 ц вычесть 12ц, чтобы получить количество картофеля на трех полях 156-12=144 ц картофеля на трех полях. А теперь мы можем 144÷3=48 ц картофеля собрали с первого и второго поля, а с третьего поля собрали 48+12=60 ц картофеля.

Ответ: с первого и второго поля собрали по 48 ц картофеля, а с третьего поля собрали 60 ц картофеля.

2 способ.

Обозначим количество картофеля собранного с первого поля буквой x ц. Тогда со второго собрали тоже x ц картофеля, а с третьего поля собрали картофеля на 12 больше, значит обозначим (x+12) ц. Количество собранного картофеля с трех полей x+x+(x+12).

По условию задачи с трех полей собрали 156 ц картофеля. Составим уравнение

 

x+x+(x+12)=156.

Отсюда 3x=144, а x =48.

 

Итак, мы получили, что с первого и второго полей собрали по 48 ц картофеля, а с третьего 48+12=60 ц картофеля.

Ответ: с первого и второго поля собрали по 48 ц картофеля, а с третьего поля собрали 60 ц картофеля.

В следующих задачах уровень сложности повышается.

№544.

1) Решите задачу.

На первом элеваторе зерна в три раза больше, чем на втором. Если с первого элеватора вывезти 850 т, а со второго – 150 т, то на обоих элеваторах зерна останется поровну. Какое количество зерна было на первом элеваторе?

Если вы догадались составить к задаче такую схему, то возможно, вы смогли решить ее устно:

 

1 элеватор		850
2 элеватор	150

 

850-150=600 т зерна в двух частях 1 элеватора;

600÷2=300 т зерна на втором элеваторе;

600+300=900 т зерна на первом элеваторе.

2) Обозначьте буквой x количество зерна на втором элеваторе. Подумайте, для каких величин можно составить выражения с этой буквой, и запишите их.

3) составьте математическую модель задачи

Пусть х – количество зерна на втором элеваторе, тогда 3х – количество зерна на первом элеваторе.

Если с первого вывезли 850 т зерна (3х-850), а со второго вывезли 150 т (х-150), то в обоих элеваторах зерна останется поровну, тогда получаем 3х-850=х-150.

Это уравнение учащиеся решить не могут, но такая задача перед ними и не ставиться, еще раз подчеркнем, что в 5 классе, главная задача научить составлять математические модели. Работать с математическими моделями они будут в следующих классах.

Следующие задачи авторы учебника предлагают решить двумя способами: арифметическим и алгебраическим. Если будут затруднения с решением уравнения, подставьте в него найденный арифметическим способом результат и проверьте справедливость составленного вами равенства. В 6-м классе дети познакомятся с методом, который позволит без труда решить все составленные ими уравнения.

№636.

Стоимость автомобиля с гаражом составляет 355600р. Сколько стоит автомобиль, если он на 97300р дороже удвоенной стоимости гаража?

Первый способ.

 

автомобиль			97300 р.
гараж

 

Вся стоимость автомобиля с гаражом 355600р.

1) 355600–97300=258300 р. цена трех гаражей;

2) 258300÷3=86100 р. стоимость гаража;

3) 355600–86100=269500 р. стоимость машины.

Ответ: стоимость автомобиля 269500 р.

2 способ.

Пусть стоимость гаража – х рублей, тогда стоимость машины – (2х+97300) р. Стоимость гаража и автомобиля вместе составляет 355600 р.

Составим уравнение:

 

х+2х+97300=355600,

3х=258300,

 

х=86100 р. – стоимость гаража, тогда стоимость автомобиля 86100×2+97300=269500р.

Ответ: стоимость автомобиля 269500 р.

№637.

В двух кусках поровну ткани. После того как от первого куска продали 14 м, а от второго – 22 м, в первом куске осталось втрое больше ткани, чем во втором. Сколько метров ткани было в каждом куске первоначально?

Решение:

1 способ.

 

 14 м

 

1 кусок
2 кусок

 

22 м

 

1 кусок
2 кусок

 

Нам известно, что ткани первоначально было поровну, затем от 1 куска отрезали 14 м, а от 2ого – 22 м, и тогда в первом куске осталось втрое больше, чем во втором. Поэтому если мы из 22 вычтем 14, то получим 8 м, а это составляет 2 одинаковых части в первом куске, значит если 8÷2=4 м осталось во втором куске, после того как от него отрезали 22 м. Значит первоначально в нем было 26 м. Можно проверить, посчитав сколько было м в первом куске: 4×3=12 м осталось в первом куске после того, как от него отрезали 14 м, и для того, чтобы найти, сколько было мы должны 14+12=26 м было в первом куске первоначально.

Ответ: первоначально в каждом куске ткани было 26 м

2 способ.

Пусть во втором осталось х м ткани, тогда в первом осталось 3х м ткани.

Мы знаем, что от первого куска отрезали 14 м, а от второго – 22 метра, тогда в 1 куске было (3х+14) м ткани, а во втором было – (х+22) м ткани.

В условии сказано, что ткани изначально было поровну, значит можем составить уравнение:

1) 3х+14=х+22,

2х=8,

х=4 м ткани осталось во втором куске,

2) 4×3=12 м ткани осталось в первом куске,

3) 4+22=26 м было в первом куске изначально.

Мы знаем, что в первом и втором кусках ткани было поровну, следовательно, и во втором куске было 26 м ткани.

Ответ: первоначально в каждом куске ткани было 26 м

№638.

У двоих братьев было вместе 112р. После того как старший отдал младшему 14 р., у него осталось все же денег больше, чем у младшего, но всего лишь на 10 р.Сколько денег было у каждого мальчика первоначально?

Решение:

1 способ.

 

 10р. 14р.

1 брат
2 брат

 

14р.

Всего у двух братьев 112 р.

 

10р.

 

1 брат
2 брат

 

14р

 

1) 112-24=88 р у двух мальчиков, после того как 1ый отдал 2ому – 14 р, и если у 1ого забрать 10 р.

2) 88÷2=44 р. стало у 2ого мальчика, когда 1ый отдал ему 14 р.,

3) 44-14=30 р. было у 2ого мальчика первоначально,

4) 44+10+14=68 р. было у первого мальчика вначале.

Ответ: у первого брата было 68 р., а у второго – 30 р.

6 класс.

§20.

В 6 классе после того как дети познакомились с действиями над положительными и отрицательными числами, научились решать уравнения, можно приступать к решению задач выделением трех этапов математического моделирования. Но решать с шестиклассниками задачи таким способом без предварительной подготовки преждевременно. Поэтому решение каждой такой задачи следует предварять специальной системой упражнений.

Например, №593.

В одном бидоне x л, а в другом – y л молока.

а) что означают выражения ?

б) что означают равенства ?

Эта задача предварительного этапа, затем следует задача №594:

В одном бидоне молока в 3 раза больше, чем в другом. когда из одного бидона перелили в другой 5 литров, молока в бидонах стало поровну. Сколько литров было в каждом бидоне первоначально?

Решите задачу алгебраическим способом.

Решение.

Пусть x л – количество молока, которое было до переливания во втором бидоне. Тогда в первом бидоне его было 3x л.

После переливания в первом бидоне осталось (3x-5) л молока, а во втором стало (x+5) л.

Поскольку после переливания в обоих бидонах молока стало поровну, можно составить уравнение:

 

3x-5=x+5.

 

Учитель сообщает, что эту часть рассуждений при решении задачи называют составлением математической модели. На этом этапе переводят текст задачи с обыденного языка на математический язык. В результате получают математическую модель ситуации, описанной в условии задачи. Такой математической моделью и является составленное уравнение. После этого приступают ко второму этапу, который называют работой с математической моделью. На этом этапе нам надо решить составленное уравнение 3x-5=x+5.

Решение (учащиеся выполняют самостоятельно):

 

3x-x=5+5,

2x=10,

x=5.

 

Уравнение решено, теперь надо приступить к третьему этапу – ответу на вопрос задачи: сколько литров было в каждом бидоне первоначально?

 Мы получили x=5, а за x было принято количество молока (в литрах), которое было во втором бидоне. Итак, во втором бидоне было 5 л молока. По условию задачи, в первом бидоне молока было в 3 раза больше, значит, в первом бидоне было 15 л молока.

Ответ: в одном бидоне было 5 л, а в другом – 15 л молока.

После этого в 7 классе повторяются этапы математического моделирования и они уже к этому подготовлены, но тем не менее нулевой этап своей актуальности не теряет, т.к. появляются более сложные задачи.

Рассмотрим задачник математика «Алгебра, 7» авторов Мордковича А.Г. и др. и составим к задачам, данным в этом учебнике, упражнения подводящие к их решению.

№95

Расстояние между городами мотоциклист проехал за 2 часа, а велосипедист – за 5 часов. Скорость велосипедиста на 18 км/ч меньше скорости мотоциклиста. найдите скорости велосипедиста и мотоциклиста и расстояние между городами.

Решение.

Т.к. скорости велосипедиста и мотоциклиста неизвестны, то мы можем взять за x – скорость мотоциклиста, а скорость велосипедиста – (x-18). Мотоциклист двигался в течение 2-х часов со скоростью x км/ч, а велосипедист – 5 ч со скоростью (x-18) км/ч. Зная, что велосипедист и мотоциклист преодолели одно и то же расстояние, составим уравнение:

 

2x=5(x-18),

3x=90,

x=30 км/ч скорость М.,

30-18=12 км/ч скорость В.

Ответ: За 2 часа мотоциклист и за 5 ч велосипедист пройдут путь в 60 км.

Но перед тем как решать эту задачу можно рассмотреть другие задачи, направленные на подготовку к ее решению:

Пешеход идет со скоростью x км/ч, велосипедист на 10 км/ч быстрее. Расстояние от точки А до точки В пешеход преодолел за 3 ч, а в