 |
Главная |
Примеры алгебраических групп матриц
|
из
5.00
|
АЛГЕБРАИЧЕСКИЕ ГРУППЫ МАТРИЦ
Исполнитель:
студентка группы H.01.01.01 М-42
Мариненко В.В.
Научный руководитель:
доктор физико-математических наук,
профессор Скиба С.В.
Гомель 2003
Содержание
Введение
1. Алгебраические группы матриц
1.1 Примеры алгебраических групп матриц
1.2 О полугруппах
1.3 Компоненты алгебраической группы
1.4 О  -группах
-группах
2 Ранг матрицы
2.1 Возвращение к уравнениям
2.2 Ранг матрицы
2.3 Критерий совместности
3 Линейные отображения. Действия с матрицами
3.1 Матрицы и отображения
3.2 Произведение матриц
3.3 Квадратные матрицы
Заключение
Список использованных источников
Введение
Множество  матриц
матриц  -ой степени над
-ой степени над  будем рассматривать как аффинное пространство
будем рассматривать как аффинное пространство  с имеющейся на ней полиномиальной топологией. Алгебраические группы матриц определяются как невырожденные части алгебраических множеств из
с имеющейся на ней полиномиальной топологией. Алгебраические группы матриц определяются как невырожденные части алгебраических множеств из  , являющиеся группами относительно обычного матричного умножения. Простейший пример такой группы - общая линейная группа
, являющиеся группами относительно обычного матричного умножения. Простейший пример такой группы - общая линейная группа  . В настоящем параграфе мы начнем систематическое изучение алгебраических матричных групп.
. В настоящем параграфе мы начнем систематическое изучение алгебраических матричных групп.
Все топологические понятия относятся к полиномиальной топологии; черта обозначает замыкание в  , диез - замыкание в
, диез - замыкание в  , бемоль - взятие невырожденной части, т. е.
, бемоль - взятие невырожденной части, т. е.  - совокупность всех невырожденных матриц из
- совокупность всех невырожденных матриц из  . Иногда, допуская вольность, мы употребляем для групп те же понятия, что и для подлежащих алгебраических множеств, - например, говорим об общих точках групп; это не должно вызывать недоразумений.
. Иногда, допуская вольность, мы употребляем для групп те же понятия, что и для подлежащих алгебраических множеств, - например, говорим об общих точках групп; это не должно вызывать недоразумений.
1. Алгебраические группы матриц
Примеры алгебраических групп матриц
Классические матричные группы - общая, специальная, симплектическая и ортогональная:

где 
 - единичная матрица и штрих обозначает транспонирование.
- единичная матрица и штрих обозначает транспонирование.
Диагональная группа  , группы клеточно-диагональных матриц данного вида. Треугольная группа
, группы клеточно-диагональных матриц данного вида. Треугольная группа  (для определенности --- с нижним нулевым углом), унитреугольная группа
(для определенности --- с нижним нулевым углом), унитреугольная группа  (треугольные матрицы с единичной диагональю), группы клеточно-треугольных матриц данного вида.
(треугольные матрицы с единичной диагональю), группы клеточно-треугольных матриц данного вида.
Централизатор произвольного множества из  в алгебраической группе
в алгебраической группе  , нормализатор замкнутого множества из
, нормализатор замкнутого множества из  в
в  .
.
Пересечение всех алгебраических групп, содержащих данное множество матриц  из
из  --- алгебраическая группа. Она обозначается
--- алгебраическая группа. Она обозначается 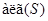 и называется алгебраической группой, порожденной множеством
и называется алгебраической группой, порожденной множеством  .
.
Каждую алгебраическую линейную группу из  можно изоморфно --- в смысле умножения и полиномиальной топологии --- отождествить с замкнутой подгруппой из
можно изоморфно --- в смысле умножения и полиномиальной топологии --- отождествить с замкнутой подгруппой из  в силу формулы
в силу формулы
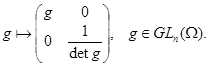
Такое отождествление позволяет при желании ограничиться рассмотрением только таких групп матриц, которые сами являются алгебраическими множествами (а не их невырожденными частями). Это дает другое оправдание тем вольностям в терминологии, которые упоминались в начале параграфа.
Множество всех матриц из  , оставляющих инвариантной заданную невырожденную билинейную форму
, оставляющих инвариантной заданную невырожденную билинейную форму  на
на  .
.
Пусть  --- алгебра над
--- алгебра над  конечной размерности
конечной размерности  (безразлично, ассоциативная или нет),
(безразлично, ассоциативная или нет),  --- группа всех ее автоморфизмов. Фиксируя в
--- группа всех ее автоморфизмов. Фиксируя в  какую-нибудь базу
какую-нибудь базу  и сопоставляя автоморфизмам алгебры
и сопоставляя автоморфизмам алгебры  их матрицы в этой базе, мы получим на
их матрицы в этой базе, мы получим на  строение алгебраической группы. Действительно, пусть
строение алгебраической группы. Действительно, пусть
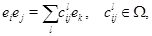
т. е.  --- структурные константы алгебры
--- структурные константы алгебры  . Пусть далее
. Пусть далее

где 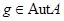 . Тогда
. Тогда  задается в матричных координатах
задается в матричных координатах  очевидными полиномиальными уравнениями, вытекающими из соотношений
очевидными полиномиальными уравнениями, вытекающими из соотношений

Указать в приведенных выше примерах определяющие уравнения, найти общую точку, если она есть.
В дальнейшем нам встретится еще много примеров и конструкций алгебраических матричных групп.
1.1.1 Если матричная группа  содержит алгебраическую подгруппу
содержит алгебраическую подгруппу 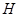 конечного индекса, то
конечного индекса, то  сама алгебраическая.
сама алгебраическая.
Доказательство. Пусть  - аннулятор группы
- аннулятор группы  в
в  ,
,  - его корень в
- его корень в  . Надо показать, что
. Надо показать, что  . Пусть, напротив,
. Пусть, напротив,  . Пусть
. Пусть  - смежные классы
- смежные классы 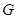 по
по  . Для каждого
. Для каждого  выберем многочлен
выберем многочлен

и положим

Очевидно,  ,
,  . Получили противоречие.
. Получили противоречие.
Пусть  --- алгебраическая группа,
--- алгебраическая группа,  ,
,  --- подмножество и замкнутое подмножество из
--- подмножество и замкнутое подмножество из  . Тогда множества
. Тогда множества

где  , замкнуты. Если
, замкнуты. Если  тоже замкнуто и
тоже замкнуто и  --- общее поле квазиопределения для
--- общее поле квазиопределения для  ,
,  ,
,  , то
, то  ,
,  ,
,  квазиопределены над
квазиопределены над  . В частности, если существует хотя бы одно
. В частности, если существует хотя бы одно  с условием
с условием  (соответственно,
(соответственно,  ,
,  ), то можно считать, что
), то можно считать, что  (см. 7.1.5).
(см. 7.1.5).
Если на множестве  выполняется теоретико-групповое тождество
выполняется теоретико-групповое тождество  , то оно выполняется и на его замыкании
, то оно выполняется и на его замыкании  . В частности, коммутативность, разрешимость, нильпотентность матричной группы сохраняются на ее замыкании в полиномиальной топологии.
. В частности, коммутативность, разрешимость, нильпотентность матричной группы сохраняются на ее замыкании в полиномиальной топологии.
О полугруппах
Определим действие элементов из  на рациональные функции из
на рациональные функции из  ,
,  , полагая
, полагая
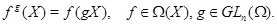
Для каждого  отображение
отображение  (сдвиг аргумента) есть автоморфизм поля
(сдвиг аргумента) есть автоморфизм поля  . Отображение
. Отображение 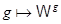 есть изоморфизм полной линейной группы
есть изоморфизм полной линейной группы  в группу автоморфизмов расширения
в группу автоморфизмов расширения  .
.
Имеет место следующее предложение.
1.2.1 Все замкнутые (в полиномиальной топологии) полугруппы из  являются группами. Более общно: замыкание
являются группами. Более общно: замыкание  произвольной полугруппы
произвольной полугруппы  --- группа. Более точно: если
--- группа. Более точно: если  --- аннулятор
--- аннулятор  в
в  , то
, то  совпадает с
совпадает с

Здесь вместо  можно написать
можно написать  .
.
Доказательство. Во-первых,  и, значит,
и, значит,  . Действительно, если
. Действительно, если  ,
, 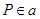 и
и  , то
, то 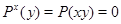 , т. е.
, т. е.  . Подпространство
. Подпространство  многочленов из
многочленов из  степени
степени  отображается оператором
отображается оператором  на себя, так как оно конечномерно, а опрератор обратим. Но тогда и всё
на себя, так как оно конечномерно, а опрератор обратим. Но тогда и всё 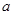 отображается на себя, как объединение всех
отображается на себя, как объединение всех  .
.
Во-вторых,  , т. е.
, т. е.  для каждого
для каждого 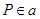 . Действительно, пусть
. Действительно, пусть 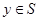 . По уже доказанному,
. По уже доказанному,  . Найдём
. Найдём  с условием
с условием  . Тогда
. Тогда 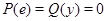 .
.
В-третьих,  , т. е.
, т. е.  для всех
для всех 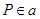 ,
,  . Действительно,
. Действительно, 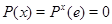 . Предложение доказано.
. Предложение доказано.
Таким образом, теория алгебраических полугрупп из  исчерпывается теорией алгебраических групп.
исчерпывается теорией алгебраических групп.
Отметим ещё одно полезное предложение.
1.2.2 Пусть алгебраическая группа  неприводима, т. е.
неприводима, т. е.  --- многообразие,
--- многообразие, 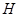 --- густое подмножество, плотное в
--- густое подмножество, плотное в  . Тогда каждый элемент
. Тогда каждый элемент 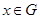 является произведением двух элементов из
является произведением двух элементов из 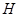 ; в частности, если
; в частности, если  --- подгруппа, то она совпадает с
--- подгруппа, то она совпадает с  .
.
Доказательство. Множества  и
и  тоже густые и плотные, поэтому пересечение
тоже густые и плотные, поэтому пересечение  непусто (см. п. 8.2).
непусто (см. п. 8.2).
Если  --- полугруппа из
--- полугруппа из 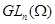 , то
, то  .
.
|
из
5.00
|
Обсуждение в статье: Примеры алгебраических групп матриц |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

