 |
Главная |
Линейные отображения. Действия с матрицами
|
из
5.00
|
Матрицы и отображения
Пусть  и
и  --- арифметические линейные пространства столбцов высоты
--- арифметические линейные пространства столбцов высоты  и
и  соответственно. Пусть, далее,
соответственно. Пусть, далее,  --- матрица размера
--- матрица размера  . Определим отображение
. Определим отображение  , полагая для любого
, полагая для любого 
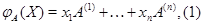
где  --- столбцы матрицы
--- столбцы матрицы  . Так как они имеют высоту
. Так как они имеют высоту  , то в правой части (1) стоит вектор-столбец
, то в правой части (1) стоит вектор-столбец 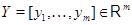 . Более подробно (1) переписывается в виде
. Более подробно (1) переписывается в виде

Если  ,
,
то  .
.
Аналогично 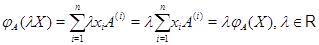 .
.
Обратно, предположим, что  --- отображение множеств, обладающее следующими двумя свойствами:
--- отображение множеств, обладающее следующими двумя свойствами:
(i)  для всех
для всех  ;
;
(ii)  для всех
для всех 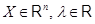 .
.
Тогда, обозначив стандартные базисные столбцы пространств  и
и  соответственно символами
соответственно символами  и
и  , мы воспользуемся свойствами (i), (ii) в применении к произвольному вектору
, мы воспользуемся свойствами (i), (ii) в применении к произвольному вектору
 :
:

Соотношение (2) показывает, что отображение  полностью определяется своими значениями на базисных векторах-столбцах. Положив
полностью определяется своими значениями на базисных векторах-столбцах. Положив

мы обнаруживаем, что задание  равносильно заданию прямоугольной матрицы
равносильно заданию прямоугольной матрицы  размера
размера  со столбцами
со столбцами  , а соотношения (1) и (2) фактически совпадают. Стало быть, можно положить
, а соотношения (1) и (2) фактически совпадают. Стало быть, можно положить  .
.
3.1.1 . Определение. Отображение  , обладающее свойствами (i), (ii), называется линейным отображением из
, обладающее свойствами (i), (ii), называется линейным отображением из  в
в  . Часто, в особенности при
. Часто, в особенности при 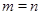 , говорят о линейном преобразовании. Матрица
, говорят о линейном преобразовании. Матрица  называется матрицей линейного отображения
называется матрицей линейного отображения 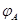 .
.
Пусть 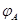 ,
,  --- два линейных отображения
--- два линейных отображения 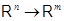 с матрицами
с матрицами  и
и  . Тогда равенство
. Тогда равенство 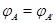 равносильно совпадению значений
равносильно совпадению значений  для всех
для всех  . В частности,
. В частности,  , откуда
, откуда 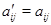 и
и  .
.
Резюмируем наши результаты:
3.1.2 Теорема. Между линейными отображениями  в
в  и матрицами размера
и матрицами размера  существует взаимно однозначное соответствие.
существует взаимно однозначное соответствие.
Следует подчеркнуть, что бессмысленно говорить о линейных отображениях  произвольных множеств
произвольных множеств  и
и  . Условия (i), (ii) предполагают, что
. Условия (i), (ii) предполагают, что  и
и  --- подпространства арифметических линейных пространств
--- подпространства арифметических линейных пространств  ,
,  .
.
Обратим внимание на специальный случай  , когда линейное отображение
, когда линейное отображение  , обычно называемое линейной функцией от
, обычно называемое линейной функцией от  переменных, задается
переменных, задается  скалярами
скалярами  :
:
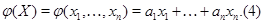
Линейные функции (4), равно как и произвольные линейные отображения  при фиксированных
при фиксированных  и
и  можно складывать и умножать на скаляры. В самом деле, пусть
можно складывать и умножать на скаляры. В самом деле, пусть  --- два линейных отображения. Отображение
--- два линейных отображения. Отображение

определяется своими значениями:

В правой части стоит обычная линейная комбинация векторов-столбцов.
Так как
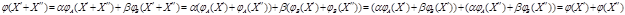

то  - линейное отображение. По теореме 1 можно говорить о его матрице
- линейное отображение. По теореме 1 можно говорить о его матрице 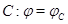 . Чтобы найти
. Чтобы найти  , выпишем, следуя (3), столбец с номером
, выпишем, следуя (3), столбец с номером  :
:

Матрицу  с элементами
с элементами  естественно назвать линейной комбинацией матриц
естественно назвать линейной комбинацией матриц  и
и  с коэффициентами
с коэффициентами  и
и  :
:


Итак, 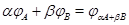 .
.
Особенно часто нами будет использоваться тот факт, что линейные комбинации линейных функций снова являются линейными функциями.
Произведение матриц
Соотношения (5) и (6) выражают согласованность действий сложения и умножения на скаляры в множествах матриц размера  и отображений
и отображений  . В случае произвольных множеств имеется еще важное понятие произведения (композиции) отображений. Разумно ожидать, что композиция двух линейных отображений должна выражаться неким согласованным образом в терминах матриц. Посмотрим как это делается.
. В случае произвольных множеств имеется еще важное понятие произведения (композиции) отображений. Разумно ожидать, что композиция двух линейных отображений должна выражаться неким согласованным образом в терминах матриц. Посмотрим как это делается.
Пусть  ,
,  --- линейные отображения,
--- линейные отображения,  --- их композиция.
--- их композиция.
Вообще говоря, нам следовало бы предварительно проверить, что  --- линейное отображение, но это довольно ясно:
--- линейное отображение, но это довольно ясно:
(i)  ;
;
(ii)  ;
;
поэтому по теореме 1 с  ассоциируется вполне определенная матрица
ассоциируется вполне определенная матрица  .
.
Действие отображений на столбцы в цепочке запишем в явном виде по формуле (  ):
):

С другой стороны,

Сравнивая полученные выражения и памятуя о том, что 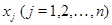 --- произвольные вещественные числа, мы приходим к соотношениям
--- произвольные вещественные числа, мы приходим к соотношениям

Будем говорить, что матрица  получается в результате умножения матрицы
получается в результате умножения матрицы  на матрицу
на матрицу  . Принято писать
. Принято писать  . Таким образом, произведением прямоугольной матрицы
. Таким образом, произведением прямоугольной матрицы  размера
размера  и прямоугольной матрицы
и прямоугольной матрицы  размера
размера  называется прямоугольная матрица
называется прямоугольная матрица  размера
размера  с элементами
с элементами  , задающимися соотношением (7). Нами доказана
, задающимися соотношением (7). Нами доказана
3.2.1 Теорема. Произведение  двух линейных отображений с матрицами
двух линейных отображений с матрицами  и
и  является линейным отображением с матрицей
является линейным отображением с матрицей  . Другими словами,
. Другими словами,

Соотношение (8) - естественное дополнение к соотношению (6).
Мы можем забыть о линейных отображениях и находить произведение  двух произвольных матриц
двух произвольных матриц  ,
,  , имея в виду, однако, что символ
, имея в виду, однако, что символ  имеет смысл только в том случае, когда число столбцов в матрице
имеет смысл только в том случае, когда число столбцов в матрице  совпадает с числом строк в матрице
совпадает с числом строк в матрице  . Именно при этом условии работает правило (7) "умножения
. Именно при этом условии работает правило (7) "умножения  -й строки
-й строки  на
на  -й столбец
-й столбец  ", согласно которому
", согласно которому
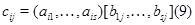
Число строк, матрицы 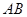 равно числу строк матрицы
равно числу строк матрицы  , а число столбцов --- числу столбцов матрицы
, а число столбцов --- числу столбцов матрицы  . В частности, произведение квадратных матриц одинаковых порядков всегда определено, но даже в этом случае, вообще говоря,
. В частности, произведение квадратных матриц одинаковых порядков всегда определено, но даже в этом случае, вообще говоря,  , как показывает хотя бы следующий пример:
, как показывает хотя бы следующий пример:

Умножение матриц, конечно, можно было бы вводить многими другими способами (умножать, например, строки на строки), но ни один из этих способов не сравним по важности с рассмотренным выше. Это и понятно, поскольку мы пришли к нему при изучении естественной композиции (суперпозиции) отображений, а само понятие отображения относится к числу наиболее фундаментальных в математике.
Следствие. Умножение матриц ассоциативно:
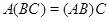
Действительно, произведение матриц соответствует произведению линейных отображений (теорема 2 и соотношение (8)), а произведение любых отображений ассоциативно. К тому же результату можно прийти вычислительным путем, используя непосредственно соотношение (7).
Квадратные матрицы
Пусть  (или
(или  ) --- множество всех квадратных матриц (
) --- множество всех квадратных матриц (  ) порядка
) порядка  с вещественными коэффициентами
с вещественными коэффициентами  ,
,
Единичному преобразованию 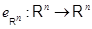 , переводящему каждый столбец
, переводящему каждый столбец  в себя, соответствует, очевидно, единичная матрица
в себя, соответствует, очевидно, единичная матрица

Можно записать  , где
, где

- символ Кронекера. Правило (7) умножения матриц, в котором следует заменить  на
на  , показывает, что справедливы соотношения
, показывает, что справедливы соотношения

Матричные соотношения (10), полученные вычислительным путем, вытекают, конечно, из соотношений  для произвольного отображения
для произвольного отображения  , если воспользоваться теоремой 1 и равенством (8) с
, если воспользоваться теоремой 1 и равенством (8) с  .
.
Как мы знаем (см. (5)), матрицы из  можно умножать на числа, понимая под
можно умножать на числа, понимая под  , где
, где  , матрицу
, матрицу  .
.
Но умножение на скаляр (число) сводится к умножению матриц:


- известная нам скалярная матрица.
В равенстве (11) отражен легко проверяемый факт перестановочности 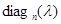 с любой матрицей
с любой матрицей  . Весьма важным для приложений является следующее его обращение.
. Весьма важным для приложений является следующее его обращение.
3.3.1 Теорема. Матрица из  , перестановочная со всеми матрицами в
, перестановочная со всеми матрицами в  , должна быть скалярной.
, должна быть скалярной.
Доказательство. Введем матрицу 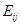 , в которой на пересечении
, в которой на пересечении  -й строки и
-й строки и  -го столбца стоит 1, а все остальные элементы --- нулевые. Если
-го столбца стоит 1, а все остальные элементы --- нулевые. Если  --- матрица, о которой идет речь в теореме, то она перестановочна,
--- матрица, о которой идет речь в теореме, то она перестановочна,

Перемножая матрицы в левой и правой частях этого равенства, мы получим матрицы

с единственным ненулевым  -м столбцом и соответственно с единственной ненулевой
-м столбцом и соответственно с единственной ненулевой 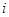 -й строкой. Их сравнение немедленно приводит к соотношениям
-й строкой. Их сравнение немедленно приводит к соотношениям  при
при  и
и  . Меняя
. Меняя 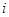 и
и  , получаем требуемое.
, получаем требуемое. 
Отметим еще соотношения  , которые непосредственно вытекают из определения умножения матриц на скаляры или, если угодно, из соотношений (11) и из ассоциативности умножения матриц.
, которые непосредственно вытекают из определения умножения матриц на скаляры или, если угодно, из соотношений (11) и из ассоциативности умножения матриц.
Для данной матрицы 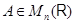 можно попробовать найти такую матрицу
можно попробовать найти такую матрицу  , чтобы выполнялось условие
, чтобы выполнялось условие

Если матрица  существует, то условию (12) в терминах линейных преобразований отвечает условие
существует, то условию (12) в терминах линейных преобразований отвечает условие

означающее, что  --- преобразование, обратное к
--- преобразование, обратное к  .
.  существует тогда и только тогда, когда
существует тогда и только тогда, когда  --- биективное преобразование. При этом
--- биективное преобразование. При этом  определено однозначно. Так как
определено однозначно. Так как  , то биективность
, то биективность  означает, в частности, что
означает, в частности, что
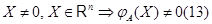
Пусть теперь  --- какое-то биективное линейное преобразование из
--- какое-то биективное линейное преобразование из  в
в  . Обратное к нему преобразование
. Обратное к нему преобразование  существует, но, вообще говоря, не ясно, является ли оно линейным. Чтобы убедиться в линейности
существует, но, вообще говоря, не ясно, является ли оно линейным. Чтобы убедиться в линейности  , мы введем векторы-столбцы
, мы введем векторы-столбцы


и применим к обеим частям этих равенств преобразование  . В силу его линейности получим
. В силу его линейности получим


Так как  , то
, то
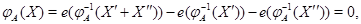
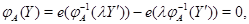
откуда, в соответствии с импликацией (13), находим, что  ,
,  --- нулевые векторы. Таким образом, выполнены свойства (i), (ii) из 3.1, определяющие линейные отображения. Имеем
--- нулевые векторы. Таким образом, выполнены свойства (i), (ii) из 3.1, определяющие линейные отображения. Имеем  , где
, где  --- некоторая матрица. Переписав условие (
--- некоторая матрица. Переписав условие ( 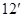 ) в виде
) в виде  (см. (8)) и снова воспользовавшись теоремой 1, мы придем к равенствам (12).
(см. (8)) и снова воспользовавшись теоремой 1, мы придем к равенствам (12).
Итак, матрица, обратная к 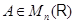 , существует в точности тогда, когда преобразование
, существует в точности тогда, когда преобразование  биективно. При этом преобразование
биективно. При этом преобразование  линейно. Биективность
линейно. Биективность  равносильна условию, что любой вектор-столбец
равносильна условию, что любой вектор-столбец  записывается единственным образом в виде (1)
записывается единственным образом в виде (1)

где  --- столбцы матрицы
--- столбцы матрицы  (сюръективность
(сюръективность  приводит к существованию
приводит к существованию  , для которого
, для которого  , а инъективность
, а инъективность  дает единственность
дает единственность  : если
: если  , то
, то  , откуда, согласно (12),
, откуда, согласно (12), 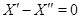 ). Значит,
). Значит, 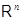 совпадает с пространством столбцов
совпадает с пространством столбцов  матрицы
матрицы  , так что
, так что 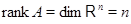 .
.
Если матрица, обратная к  , существует, то, согласно вышесказанному, она единственна. Ее принято обозначать символом
, существует, то, согласно вышесказанному, она единственна. Ее принято обозначать символом  . В таком случае (см. (
. В таком случае (см. (  ))
))

Квадратную матрицу  , для которой существует обратная матрица
, для которой существует обратная матрица  , называют невырожденной (или неособенной). Невырожденным называют и соответствующее линейное преобразование
, называют невырожденной (или неособенной). Невырожденным называют и соответствующее линейное преобразование  . В противном случае матрицу
. В противном случае матрицу  и линейное преобразование
и линейное преобразование  называют вырожденными (или особенными).
называют вырожденными (или особенными).
Резюмируем полученные нами результаты.
3.3.2 Теорема. Квадратная матрица  порядка
порядка  является невырожденной тогда и только тогда, когда ее ранг равен
является невырожденной тогда и только тогда, когда ее ранг равен  . Преобразование
. Преобразование  , обратное к
, обратное к  , линейно и задается равенством (14).
, линейно и задается равенством (14).
Следствие. Невырожденность  влечет невырожденность
влечет невырожденность  и
и  . Если
. Если  --- невырожденные
--- невырожденные  --- матрицы, то произведение
--- матрицы, то произведение  также невырождено и
также невырождено и 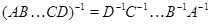 .
.
Для доказательства достаточно сослаться на симметричность условия 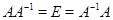 .
. 
Нами получено довольно много правил действий с квадратными матрицами порядка  . Имеются в виду, ассоциативность (следствие теоремы 2), (10) и теорема 4. Обратим еще внимание на так называемые законы дистрибутивности:
. Имеются в виду, ассоциативность (следствие теоремы 2), (10) и теорема 4. Обратим еще внимание на так называемые законы дистрибутивности:

где  ,
,  ,
,  --- произвольные матрицы из
--- произвольные матрицы из  .
.
Действительно, полагая  , мы получим для любых
, мы получим для любых  равенство (используется дистрибутивность в
равенство (используется дистрибутивность в  ):
):

левая часть которого дает элемент  матрицы
матрицы  , а правая --- элементы
, а правая --- элементы  и
и  матриц
матриц  и соответственно
и соответственно  . Второй закон дистрибутивности (16) проверяется совершенно аналогично. Необходимость в нем обусловлена некоммутативностью умножения в
. Второй закон дистрибутивности (16) проверяется совершенно аналогично. Необходимость в нем обусловлена некоммутативностью умножения в  . Законы дистрибутивности
. Законы дистрибутивности

для линейных отображений  ,
, 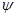 ,
,  из
из  в
в 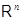 можно не доказывать, ссылаясь на соответствие между отображениями и матрицами, но можно, в свою очередь, выводить (16) из (
можно не доказывать, ссылаясь на соответствие между отображениями и матрицами, но можно, в свою очередь, выводить (16) из (  ), поскольку в случае отображений, рассуждение столь же просто.
), поскольку в случае отображений, рассуждение столь же просто.
Заключение
Таким образом, в данной курсовой работе мы доказали, что связанная компонента единицы алгебраической группы содержится в любой замкнутой подгруппе конечного индекса. В работе была доказана теорема: Для любой прямоугольной  -матрицы
-матрицы  справедливо равенство
справедливо равенство  (это число называется просто рангом матрицы
(это число называется просто рангом матрицы  и обозначается символом
и обозначается символом  ).А также было получено эффективное средство для вычисления ранга матрицы
).А также было получено эффективное средство для вычисления ранга матрицы  , устраняющее необходимость приведения
, устраняющее необходимость приведения  к ступенчатому виду, доказана теорема: Квадратная матрица
к ступенчатому виду, доказана теорема: Квадратная матрица  порядка
порядка  является невырожденной тогда и только тогда, когда ее ранг равен
является невырожденной тогда и только тогда, когда ее ранг равен  . Преобразование
. Преобразование  , обратное к
, обратное к  , линейно и задается равенством (14) и следствие этой теоремы: невырожденность
, линейно и задается равенством (14) и следствие этой теоремы: невырожденность  влечет невырожденность
влечет невырожденность 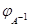 и
и  . Если
. Если  --- невырожденные
--- невырожденные  --- матрицы, то произведение
--- матрицы, то произведение  также невырождено и
также невырождено и  .
.
|
из
5.00
|
Обсуждение в статье: Линейные отображения. Действия с матрицами |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

