Компоненты алгебраической группы

Пусть  --- алгебраическая группа матриц. Невырожденные части компонент её подлежащего многообразия  называеются компонентами группы . наличие в  групповой структуры позволяет высказать о компонентах ряд важных утверждений, отсутствующих в случае произвольного многообразия.

1.3.1 Теорема. Пусть  --- алгебраическая группа матриц. Её компонента , содержащая единицу, единственна и является нормальной подгруппой. Остальные компоненты --- смежные классы  по  (в частности, они являются связными компонентами группы  в полиномиальной топологии).  --- единственная связная замкнутая подгруппа конечного индекса в . Аннулятор  компоненты  связан с аннулятором 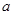 всей группы  следующим образом:

 для некоторого , зависящего от  

, где  --- аннулятор единицы в ,  --- некоторый многочлен из .

Доказательство. а) Пусть  --- общее поле определения всех компонент  группы . Пусть ,  содержат единицу , ,  --- их независимые общие точки над  и , . Имеем специализации

над , откуда , , . Этим доказана единственность компоненты .

б) Очевидно, что отображения

являются гомеоморфизмами пространства . Так как 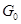 инвариантна относительно них, то  --- нормальная подгруппа группы .

в) Пусть . Тогда  при фиксированном  --- снова все компоненты группы . В частности, , . Этим доказано, что  --- смежные классы  по  и, значит, связные компоненты группы .

г) Если  --- связная замкнутая подгруппа группы , то, предыдущему, . Если, кроме того,  конечного индекса, то она той же размерности, что и 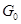, потому совпадает с .

д) Для каждого  возьмем многочлен

Пусть  --- точка из , в которой . Рассмотрим многочлен

Он искомый. В самом деле, очевидно, . Оба включения справа налево очевидны (использовать простоту идеала ). Остается доказать включение

Пусть , . Имеем:

Если , то , если же , , 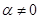то . В любом случае . Следовательно, . Теорема доказана.

Мы видим, в частности, что для алгебраической группы неприводимость и связность в полиномиальной топологии --- одно и то же; в дальнейшем мы будем пользоваться только вторым термином, чтобы избежать путаницы с понятием матричной приводимости групп (к полураспавшейся форме).

Доказать, что связанная компонента единицы алгебраической группы содержится в любой замкнутой подгруппе конечного индекса.

Подгруппа  алгебраической группы  тогда и только тогда замкнута, когда замкнуто её пересечение со связной компонентой единицы .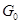

<<Только тогда>> очевидно. <<Тогда>> вытекает из 9.1.9, если заметить, что

Конечная нормальная подгруппа  связной алгебраической группы  всегда лежит в центре .

В заключение отметим, что если в качестве универсальной области выбрано поле комплексных чисел , то в алгебраической группе можно рассматривать две топологии --- полиномиальную и евклидову. Ясно, что вторая тоньше первой, поэтому, в частности, евклидова связная компонента единицы содержится в полиномиальной связной компоненте. Можно было бы доказать и обратное, т. е. на самом деле связные компоненты комплексной алгебраической группы в обеих топологиях одни и те же. Этот результат становится неверным, если рассматривать -порцию комплексной алгебраической группы (по поводу определения см. следующий пункт).

1.4. О -группах

Пусть  - поле. По определению, алгебраическая -группа --- это группа матриц из , выделяемая полиномиальными уравнениями с коэффициентами в . Иначе можно сказать, что это -порция, т. е. пересечение с , некоторой алгебраической группы, квазиопределенной над . Обычные алгебраические группы тоже можно трактовать как -группы по отношению к некоторой большей универсальной области . В этом смысле понятие алгебраической -группы является более общим, так как от  не требуется ни алгебраической замкнутости, ни бесконечной степени трансцендентности над простым полем.

В свойствах алгебраических групп и -групп много общего. Имеется сандартный способ перехода от первых ко вторым --- посредством поля определения (в чём и состоит основное значение этого понятия). Нам не раз представится возможность продемонстрировать этот способ. В целом же -группы в нашем изложении останутся на заднем плане, лишь иногда выходя на авансцену.

Многие результаты о -группах по формулировке и доказательству вполне аналогичны результатам об абсолютных алгебраических группах (в ) и опираются на сведения из алгебраической геометрии для -множеств, (по определению, алгебраическое -множество выделяется в  уравнениями с коэффициентами из ).

Ранг матрицы