 |
Главная |
Глава 3. Интегрально исчисление
|
из
5.00
|
Неопределенный интеграл
Определения и свойства
Определение 1. Функция  называется первообразной для
называется первообразной для  , если
, если  .
.
Определение 2. Неопределенным интегралом от функции f(x) называется совокупность всех первообразных для этой функции.
Обозначение:  , где c - произвольная постоянная.
, где c - произвольная постоянная.
Свойства неопределенного интеграла
1. Производная неопределенного интеграла: 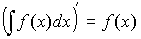
2. Дифференциал неопределенного интеграла: 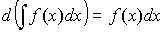
3. Неопределенный интеграл от дифференциала: 
4. Неопределенный интеграл от суммы (разности) двух функций:
 ;
;
5. Вынесение постоянного множителя за знак неопределенного интеграла:

Таблица интегралов







Основные методы интегрирования
1. Использование свойств неопределенного интеграла.
Пример 29.


2. Подведение под знак дифференциала.
Пример 30.

3. Метод замены переменной:
а) замена  в интеграле
в интеграле
 :
: 
 ,
,
где  - функция, интегрируемая легче, чем исходная;
- функция, интегрируемая легче, чем исходная;  - функция, обратная функции
- функция, обратная функции  ;
;  - первообразная функции
- первообразная функции  .
.
Пример 31.


б) замена  в интеграле вида:
в интеграле вида:
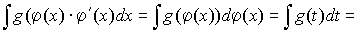
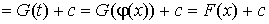 ;
;
Пример 32.



Пример 33.
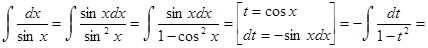

4. Метод интегрирования по частям:

Пример 34.


Пример 35.


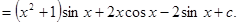
Возьмем отдельно интеграл


Вернемся к нашему интегралу:
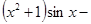
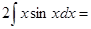


Определенный интеграл
Понятие определенного интеграла и его свойства
Определение. Пусть на некотором интервале  задана непрерывная функция
задана непрерывная функция  . Построим ее график.
. Построим ее график.

Фигура, ограниченная сверху кривой  , слева и справа прямыми
, слева и справа прямыми 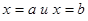 и снизу отрезком оси абсцисс между точками a и b, называется криволинейной трапецией.
и снизу отрезком оси абсцисс между точками a и b, называется криволинейной трапецией.
S – область – криволинейная трапеция.
Разделим интервал точками  и получим:
и получим:

Интегральная сумма:


Определение. Определенным интегралом называется предел интегральной суммы.
Свойства определенного интеграла:
1. Постоянный множитель можно выносить за знак интеграла:
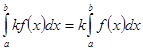
2. Интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов этих функций:

3. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е. при любых a, b, c  :
:

4. Если на отрезке 
 , то и
, то и 

5. Пределы интегрирования можно менять местами, при этом меняется знак интеграла:
6. 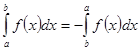
7. Интеграл в точке равен 0:

8. 
9. (“о среднем”) Пусть y = f(x) – функция, интегрируемая на [a,b]. Тогда  , где
, где  , f(c) – среднее значение f(x) на [a,b]:
, f(c) – среднее значение f(x) на [a,b]:

10. Формула Ньютона-Лейбница
 ,
,
где F(x) – первообразная для f(x).
Методы вычисления определенного интеграла.
1. Непосредственное интегрирование
Пример 35.
а) 
б) 
в) 

д) 
2. Замена переменных под знаком определенного интеграла.


Пример 36.

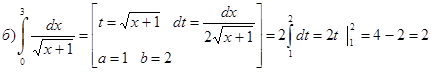
2. Интегрирование по частям в определенном интеграле.

Пример 37.
а) 
б) 

в) 
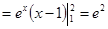

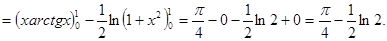
д) 
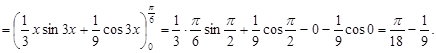
|
из
5.00
|
Обсуждение в статье: Глава 3. Интегрально исчисление |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

