 |
Главная |
Оценка тесноты связи изучаемых признаков на основе линейного коэффициента корреляции (в предположении, что взаимосвязь признаков линейная)
|
из
5.00
|
В случае линейной связи факторного и результативного признаков оценить тесноту связи можно не только с помощью значения корреляционного отношения, но и используя линейный коэффициент корреляции r. Для определения тесноты связи на основе коэффициента r в Excel используется инструмент Корреляция.
Результатом работы инструмента Корреляция является таблица, содержащая рассчитанные линейные коэффициенты корреляции. В нашем случае корреляция парная, результативная таблица имеет вид:
|
|
| Таблица 2.5 |
| Линейный коэффициент корреляции признаков | ||
| Столбец 1 | Столбец 2 | |
| Столбец 1 | 1 |
|
| Столбец 2 | 0,195302983 | 1 |
Таким образом, можно сделать вывод, что связь между признаками прямая, незаметная (т.к. r = 0,195). Кроме того, с уверенностью можно утверждать, что взаимосвязь признаков криволинейная (т.к. r ≠ η).
Построение однофакторной линейной регрессионной модели связи изучаемых признаков с помощью инструмента Регрессия
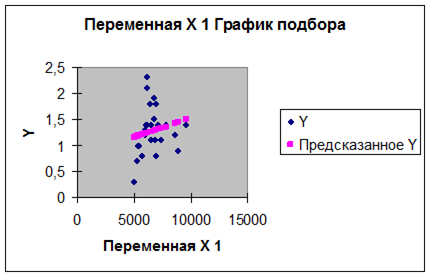
Регрессионный анализ заключается в определении аналитического выражения связи между факторным признаком Х и результативным признаком Y . В результате работы инструмента Регрессия Excel формирует следующий набор из четырех таблиц и одного графика:
1. Таблица Регрессионная статистика – содержит линейный коэффициент корреляции r, коэффициент детерминации R2 , количество наблюдений n, среднее квадратическое отклонение расчетных значений от фактических (стандартная ошибка) 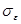 :
:
| ВЫВОД ИТОГОВ |
|
|
|
|
| Регрессионная статистика | |
| Множественный R | 0,195302983 |
| R-квадрат | 0,038143255 |
| Нормированный R-квадрат | 0,001148765 |
| Стандартная ошибка | 0,437802577 |
| Наблюдения | 28 |
2. Таблица Дисперсионный анализ – содержит значения факторной и остаточной дисперсий 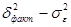 (графа MS) и другие параметры дисперсионного анализа:
(графа MS) и другие параметры дисперсионного анализа:
| Дисперсионный анализ | |||||
| df | SS | MS | F | Значимость F | |
| Регрессия | 1 | 0,19762293 | 0,19762293 | 1,031052328 | 0,319268159 |
| Остаток | 26 | 4,983448499 | 0,191671096 |
|
|
| Итого | 27 | 5,181071429 |
|
|
|
3. Результативная таблица – содержит значения параметров а0 (свободный член регрессии), а1 (коэффициент регрессии) уравнения регрессии и их статистические оценки, включая границы доверительных интервалов для коэффициентов уравнения регрессии:
| Коэффициенты | Стандартная ошибка | t-статистика | ||||
| Y-пересечение | 0,770797654 | 0,496460019 | 1,552587568 | |||
| Переменная X 1 | 7,62662E-05 | 7,5109E-05 | 1,015407469 | |||
| P-Значение | Нижние 95% | Верхние 95% | Нижние 68,3% | Верхние 68,3% | ||
| 0,132610618 | -0,249690521 | 1,791285829 | 0,264273679 | 1,277321629 | ||
| 0,319268159 | -7,81225E-05 | 0,000230655 | -3,65327E-07 | 0,000152898 | ||
4. Таблица Вывод остатка – содержит рассчитанные (сглаженные, предсказанные) значения 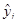 (расчетные значения результативного признака) и значения остатков
(расчетные значения результативного признака) и значения остатков 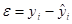 (отклонения расчетных значений от фактических):
(отклонения расчетных значений от фактических):
| ВЫВОД ОСТАТКА |
| |
|
|
|
|
| Наблюдение | Предсказанное Y | Остатки |
| 1 | 1,1527769 | -0,8527769 |
| 2 | 1,16308809 | 0,03691191 |
| 3 | 1,170074073 | -0,470074073 |
| 4 | 1,181277577 | -0,181277577 |
| 5 | 1,184968861 | -0,184968861 |
| 6 | 1,18842372 | 0,01157628 |
| 7 | 1,205194657 | -0,405194657 |
| 8 | 1,208146158 | -0,408146158 |
| 9 | 1,224177313 | -0,024177313 |
| 10 | 1,226457672 | 0,073542328 |
| 11 | 1,233489416 | 0,166510584 |
| 12 | 1,239811883 | 1,060188117 |
| 13 | 1,240597425 | 0,859402575 |
| 14 | 1,240864357 | 0,159135643 |
| 15 | 1,259847013 | 0,540152987 |
| 16 | 1,265483085 | -0,165483085 |
| 17 | 1,269075223 | 0,130924777 |
| 18 | 1,287531643 | 0,212468357 |
| 19 | 1,287981613 | 0,612018387 |
| 20 | 1,295829405 | -0,195829405 |
| 21 | 1,299276637 | -0,499276637 |
| 22 | 1,300146071 | 0,499853929 |
| 23 | 1,309725106 | 0,090274894 |
| 24 | 1,332589712 | -0,232589712 |
| 25 | 1,362997044 | 0,037002956 |
| 26 | 1,426374254 | -0,226374254 |
| 27 | 1,444068011 | -0,544068011 |
| 28 | 1,499727081 | -0,099727081 |
|
из
5.00
|
Обсуждение в статье: Оценка тесноты связи изучаемых признаков на основе линейного коэффициента корреляции (в предположении, что взаимосвязь признаков линейная) |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

