 |
Главная |
Предварительные сведения
|
из
5.00
|
Содержание
О теории нумераций
Предварительные сведения
Вычислимые нумерации
Основные понятия
Главные нумерации
Отделимые нумерации
Минимальные нумерации
Категория нумерованных множеств
Нумерации множества и его подмножеств
Категория нумерованных множеств и ее свойства
Список литературы
О теории нумераций
Представляется желательным, чтобы все исследования в теории алгоритмов и ее приложениях проводились на основе «общего знаменателя» – класса всех частично рекурсивных функций. Одним из способов такой редукции к натуральным числам и арифметическим функциям является использование подходящей нумерации.
Нумерация – это отображение некоторого подмножества множества натуральных чисел N на исследуемый класс конструктивных объектов (формул, слов, матриц и т.п.)
Теория нумераций является разделом теории алгоритмов призванным решить вопросы, связанные с приведением к «общему знаменателю» на основе понятия нумерованного множества. В теории нумераций разрабатывается необходимая система понятий, ставятся и решаются вопросы, такие как, например, зависимость или независимость тех или иных свойств множества от выбора нумерации, существование (единственность) нумерации с заданными свойствами.
Общая теория нумераций возникла в феврале 1954 года в результате замечания, сделанного Колмогоровым на семинаре по рекурсивной арифметике. Поводом послужило изучение на указанном семинаре так называемых конструктивных ординалов (конструктивных порядковых чисел), т.е. тех ординалов, которых можно снабдить именами, используя некоторую алгоритмическую процедуру. Основные понятия теории нумераций были сформулированы Колмогоровым при обсуждении этой темы.
Результаты теории нумераций оказались важными для прояснения ряда трудностей, возникающих при эксплуатации вычислительной техники. Например, одной из важных задач программирования является задача эффективного построения по программе вычисления функции на одной машине программы вычисления той же функции на другой машине. Практическая реализация этих «переводов» («трансляций») для двух универсальных машин оказывается весьма сложной, а часто и не осуществленной.
Под «универсальной вычислительной машиной» будем понимать машину, вычисляющую некоторую двуместную функцию  , универсальную для класса всех одноместных частично рекурсивных функций, а под «программой вычисления одноместной частично рекурсивной функции
, универсальную для класса всех одноместных частично рекурсивных функций, а под «программой вычисления одноместной частично рекурсивной функции  » будем понимать ее номер
» будем понимать ее номер  (один из ее номеров), т.е. такое число n
(один из ее номеров), т.е. такое число n 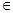 N, что таким образом, если имеются две универсальные вычислительные машины (т.е. две универсальные функции
N, что таким образом, если имеются две универсальные вычислительные машины (т.е. две универсальные функции  ), то «проблема перевода» может быть сформулирована как проблема существования одноместной общерекурсивной функции f такой что
), то «проблема перевода» может быть сформулирована как проблема существования одноместной общерекурсивной функции f такой что 
Однако, как показывают исследования вычислимых нумераций, существуют такие универсальные функции  , что желаемой функции f не существует. Более того, существуют и такие
, что желаемой функции f не существует. Более того, существуют и такие  что невозможен ни перевод с
что невозможен ни перевод с  , ни наоборот.
, ни наоборот.
Тем не менее, в классе так определенных универсальных машин существует «самая» универсальная (которую, по-видимому, только и стоит называть универсальной) в том смысле, что на язык этой машины может быть осуществлен перевод с любой другой универсальной машины. Если же рассматривать машины, которые вычисляют только общерекурсивные (всюду определенные) функции из некоторого достаточно богатого класса, то ситуация становится еще более плохой. Для любой такой машины существует другая машина, вычисляющая тот же класс функций, такая, что обе проблемы перевода неразрешимы. Указанный только что подход к разъяснению трудностей перевода может быть использован для определения понятия сложности класса функций (с помощью полурешетки вычислимых нумераций этого класса).
Такое понятие сложности класса функций может, по-видимому, во многих вопросах быть более полезным, чем изучаемые сейчас различные понятия сложности отдельно взятых функций.
Предварительные сведения
Через O обозначим класс всех одноместных общерекурсивных функций, а через O – класс всех одноместных однозначных общерекурсивных функций.
Двуместная функция с определенная так  , называется канторовской нумерующей функцией. Оно осуществляет взаимно-однозначное отображение
, называется канторовской нумерующей функцией. Оно осуществляет взаимно-однозначное отображение  . Существуют однозначно определенные функции r,
. Существуют однозначно определенные функции r,  такие что
такие что

для любых  .
.
Используя канторовскую функцию с, можно определить последовательность общерекурсивных функций  такую что
такую что  - n‑местная функция, осуществляющая взаимно-однозначное отображение
- n‑местная функция, осуществляющая взаимно-однозначное отображение  :
:
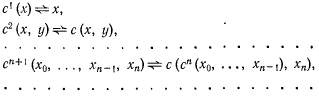
Для любого  существует набор
существует набор  из n одноместных функций такой, что выполнены тождества
из n одноместных функций такой, что выполнены тождества

Функцию  назовем сверткой, а набор
назовем сверткой, а набор  – n‑разверткой.
– n‑разверткой.
Если  Если f – функция, то график f множество
Если f – функция, то график f множество  . Будем говорить что множество А m‑сводится к В (символически
. Будем говорить что множество А m‑сводится к В (символически  ), если существует
), если существует  O такая что
O такая что  для любого
для любого  . Всякую функцию
. Всякую функцию  O удовлетворяющую этому условию называют сводящей (А к В). Еще говорят что f m‑сводит к А к В.
O удовлетворяющую этому условию называют сводящей (А к В). Еще говорят что f m‑сводит к А к В.
Категория  – это класс ObR объектов R вместе с классом MorR морфизмов R со следующими структурами на этих классах:
– это класс ObR объектов R вместе с классом MorR морфизмов R со следующими структурами на этих классах:
1. С каждой парой 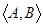 объектов R связано множество Mor (A, B)
объектов R связано множество Mor (A, B)  MorR множество всех морфизмов из А в В;
MorR множество всех морфизмов из А в В;
И если 
 ,
,  то
то
2. С каждой тройкой  объектов R связано отображение
объектов R связано отображение  :
:  так что для A, B, C, D
так что для A, B, C, D 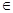 ObR, если
ObR, если  Mor (A, B),
Mor (A, B),  Mor (B, C),
Mor (B, C),  Mor (C, D), то
Mor (C, D), то 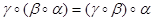
3. Для каждого А 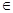 ObR в Mor (A, A) выделен элемент
ObR в Mor (A, A) выделен элемент  такой что для любого B
такой что для любого B 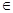 ObR, любого
ObR, любого  выполняются равенства
выполняются равенства 
Основные понятия
Пусть  ,
,  , – семейство всех рекурсивно перечислимых множеств n‑ок натуральных чисел; вместо
, – семейство всех рекурсивно перечислимых множеств n‑ок натуральных чисел; вместо  часто употребляется просто
часто употребляется просто  .
.
Пусть  – семейство рекурсивно перечислимых подмножеств N. Нумерацию
– семейство рекурсивно перечислимых подмножеств N. Нумерацию  этого семейства назовем вычислимой, если множество
этого семейства назовем вычислимой, если множество  рекурсивно перечислимо (т.е.
рекурсивно перечислимо (т.е. 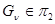 ).
).
Распространим введенное определение на нумерации семейств  .
.
Нумерация  семейства
семейства  , называется вычислимой, если множество
, называется вычислимой, если множество 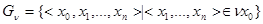 рекурсивно перечислимо (
рекурсивно перечислимо (  ).
).
Предложение 1:
Нумерация  ,
,  , вычислима тогда и только тогда, когда нумерация
, вычислима тогда и только тогда, когда нумерация  свертки семейства
свертки семейства  , определенная так
, определенная так  , является вычислимой. Нумерация
, является вычислимой. Нумерация  ,
,  является вычислимой тогда и только тогда, когда нумерация
является вычислимой тогда и только тогда, когда нумерация  n‑развертки семейства
n‑развертки семейства  определенная так
определенная так  является вычислимой.
является вычислимой.
Обозначим через 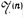 , n
, n  , семейство всех n‑местных частично рекурсивных функций, через
, семейство всех n‑местных частично рекурсивных функций, через  – отображение, сопоставляющее функции ее график.
– отображение, сопоставляющее функции ее график.
Пусть  – семейство n‑местных частично рекурсивных функций. Нумерацию
– семейство n‑местных частично рекурсивных функций. Нумерацию  семейства
семейства  назовем вычислимой, если нумерация
назовем вычислимой, если нумерация  семейства графиков функций из
семейства графиков функций из  , определенная так
, определенная так  является вычислимой.
является вычислимой.
Предложение 2
Нумерация  семейства n‑местных частично-рекурсивных функций вычислимая тогда и только тогда когда частичная (n+1) – местная функция
семейства n‑местных частично-рекурсивных функций вычислимая тогда и только тогда когда частичная (n+1) – местная функция  определенная соотношением
определенная соотношением  является частично-рекурсивной.
является частично-рекурсивной.
Функция  , связанная с нумерацией
, связанная с нумерацией  некоторого семейства
некоторого семейства  частично-рекурсивных функций является универсальной функцией для
частично-рекурсивных функций является универсальной функцией для  , т.е. для любого
, т.е. для любого  функция
функция  принадлежит
принадлежит  и наоборот, для всякой функции
и наоборот, для всякой функции  существует
существует  такое что
такое что  .
.
Всякая универсальная функция F для семейства  определяет некоторую нумерацию
определяет некоторую нумерацию  семейства
семейства  так:
так:  . Эта нумерация вычислима тогда и только тогда, когда F частично рекурсивна.
. Эта нумерация вычислима тогда и только тогда, когда F частично рекурсивна.
Семейство  называется вычислимым если существует по крайней мере одна вычислимая нумерация семейства
называется вычислимым если существует по крайней мере одна вычислимая нумерация семейства  .
.
Пусть  – две нумерации одного и того же множества S. Говорят что нумерация
– две нумерации одного и того же множества S. Говорят что нумерация  сводится к нумерации
сводится к нумерации  , если существует
, если существует  такая что
такая что  . Если
. Если  сводится к
сводится к  , то символически изображаем это так
, то символически изображаем это так 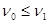 .
.
Отношение  , определенное на множестве H(S) всех нумераций множества S является транзитивным. Следовательно, отношение
, определенное на множестве H(S) всех нумераций множества S является транзитивным. Следовательно, отношение  на H(S) является предпорядком.
на H(S) является предпорядком.
Если  и
и  для
для  , то эти нумерации эквивалентны и обозначаются
, то эти нумерации эквивалентны и обозначаются  . Класс нумераций эквивалентных нумерации
. Класс нумераций эквивалентных нумерации 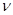 обозначим через [
обозначим через [ 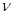 ]. Множество классов эквивалентных нумераций обозначим через L(S).
]. Множество классов эквивалентных нумераций обозначим через L(S).
На множестве H(S) можно задать операцию прямой суммы нумераций  . Пусть нумерации
. Пусть нумерации  , определим нумерацию
, определим нумерацию  следующим образом:
следующим образом:

Основное свойство операции следующее:
Предложение 3
Пусть  тогда
тогда  сводится к
сводится к 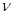 тогда и только тогда когда
тогда и только тогда когда  сводится к
сводится к 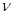 и
и  сводится к
сводится к 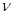 .
.
Обозначим через  семейство всех вычислимых нумераций
семейство всех вычислимых нумераций  и через
и через  семейство классов эквивалентных вычислимых нумераций
семейство классов эквивалентных вычислимых нумераций  .
.
Главные нумерации
Рассмотрим понятие главной нумерации для семейства рекурсивно перечислимых множеств. Это понятие позволяет ответить (в случае семейства рекурсивно перечислимых множеств) на вопрос: «какую нумерацию данного множества следует считать наиболее естественной?»
Нумерацию  назовем главной, если любая нумерация
назовем главной, если любая нумерация  сводится к
сводится к  .
.
Нумерацию  назовем минимальной, если
назовем минимальной, если  следует что
следует что  .
.
У семейства  может существовать не более одной с точностью до эквивалентности главной нумерации. Минимальных нумераций может существовать очень много.
может существовать не более одной с точностью до эквивалентности главной нумерации. Минимальных нумераций может существовать очень много.
Предложение 1
Семейства  обладают главными вычислимыми нумерациями.
обладают главными вычислимыми нумерациями.
Семейство  назовем главным подмножеством, если оно обладает главной вычислимой нумерацией.
назовем главным подмножеством, если оно обладает главной вычислимой нумерацией.
Предложение 2
Главное подмножество 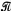 замкнуто относительно объединения возрастающих вычислимых последовательностей своих элементов.
замкнуто относительно объединения возрастающих вычислимых последовательностей своих элементов.
Семейство  назовем
назовем  -подмножеством
-подмножеством 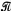 , если существует частично рекурсивная функция g такая что выполнены условия:
, если существует частично рекурсивная функция g такая что выполнены условия:
1. если  то
то  ;
;
2. если  , то
, то  и
и 
Предложение 3
Всякое непустое  -подмножеством является главным.
-подмножеством является главным.
Существуют естественные классы рекурсивно перечислимых множеств, которые не имеют главной вычислимой нумерации. Таковыми, например, являются любые семейства общерекурсивных функций.
Определим понятие предельной точки для семейства  .
.
Одноместная (всюду определенная) функция h называется предельной точкой для семейства S, если для любого n  N в S найдется функция g отличная от h такая что
N в S найдется функция g отличная от h такая что  .
.
Предложение 4
Если вычислимое семейство  содержит предельную точку, то S не имеет главной вычислимой нумерации.
содержит предельную точку, то S не имеет главной вычислимой нумерации.
Следствие
Семейство всех одноместных примитивно рекурсивных функций не имеет главной вычислимой нумерации.
Отделимые нумерации
Во многих вопросах, связанных с употреблением нумераций, важно знать, какие отношения между элементами нумерованного множества можно эффективно распознать по их номерам. Одним из самых первых вопросов является следующий: можно ли по номерам двух элементов эффективно узнать, являются ли они Равными или нет? Те нумерации, для которых этот вопрос решается положительно, называются разрешимыми.
Пусть  – нумерация множества S. Рассмотрим бинарное отношение
– нумерация множества S. Рассмотрим бинарное отношение  на множестве N определенное так
на множестве N определенное так  . Отношение
. Отношение  является отношением эквивалентности и называется нумерационной эквивалентностью. Нумерация
является отношением эквивалентности и называется нумерационной эквивалентностью. Нумерация  называется разрешимой, если отношение
называется разрешимой, если отношение  рекурсивно. Нумерацию
рекурсивно. Нумерацию  называется позитивной (негативной) если
называется позитивной (негативной) если  (
(  ) рекурсивно перечислимо.
) рекурсивно перечислимо.
Отношение эквивалентности  (
(  ) на множестве S называется разрешимым (позитивным, негативным), если S рекурсивно (рекурсивно перечислимо, представляет собой дополнение до рекурсивно перечислимого множества).
) на множестве S называется разрешимым (позитивным, негативным), если S рекурсивно (рекурсивно перечислимо, представляет собой дополнение до рекурсивно перечислимого множества).
Таким образом, нумерация  разрешима (позитивна, негативна) тогда и только тогда когда таковой является ее нумерационная эквивалентность.
разрешима (позитивна, негативна) тогда и только тогда когда таковой является ее нумерационная эквивалентность.
Предложение 1
Нумерация  бесконечного множества S является разрешимой тогда и только тогда когда она эквивалентна некоторой однозначной нумерации.
бесконечного множества S является разрешимой тогда и только тогда когда она эквивалентна некоторой однозначной нумерации.
Предложение 2
Если  – позитивное (негативное) отношение эквивалентности, то
– позитивное (негативное) отношение эквивалентности, то  - нумерационная эквивалентность подходящей вычислимой нумерации
- нумерационная эквивалентность подходящей вычислимой нумерации
Предложение 3
Если  - семейство попарно не пересекающихся непустых рекурсивно перечислимых множеств, а
- семейство попарно не пересекающихся непустых рекурсивно перечислимых множеств, а  - вычислимая нумерация, то
- вычислимая нумерация, то  позитивна
позитивна
Предложение 4
Если  – семейство общерекурсивных функций,
– семейство общерекурсивных функций,  – вычислимая нумерация, то
– вычислимая нумерация, то  - негативная нумерация.
- негативная нумерация.
Отметим некоторые свойства позитивных и негативных нумераций относительно сводимости.
Предложение 5
Если S – бесконечное множество, 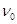 – негативная нумерация S, то существует однозначная нумерация
– негативная нумерация S, то существует однозначная нумерация  множества S такая что
множества S такая что 
Предложение 6
Пусть S – бесконечное множество, 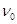 - позитивная нумерация множества S. Если существует однозначная нумерация
- позитивная нумерация множества S. Если существует однозначная нумерация  множества S такая что
множества S такая что  , то
, то  – разрешимая нумерация.
– разрешимая нумерация.
Предложение 7
Пусть 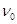 – позитивная нумерация S и
– позитивная нумерация S и  , тогда
, тогда 
Следствие
Позитивные нумерации множества определяют минимальные элементы в L( S )
Минимальные нумерации
Настоящий параграф посвящен краткому обзору (без доказательств) результатов, связанных с изучением вопроса о существовании тех или иных вычислимых минимальных нумераций у различных классов рекурсивно перечислимых множеств.
Нумерация ν: N →  некоторого множества
некоторого множества  называется однозначной, если ν n ≠ ν m для n ≠ m
называется однозначной, если ν n ≠ ν m для n ≠ m  N.
N.
Интерес к изучению вопроса о существовании однозначных вычислимых нумераций у семейства  объясняется такими обстоятельствами:
объясняется такими обстоятельствами:
1. Всякая однозначная нумерация ν минимальна, т.е. [ν] – минимальный элемент в L °( S ).
2. Если семейство S имеет хотя бы одну вычислимую однозначную нумерацию, то для любого R 
 семейство
семейство  \ { R } вычислимо (даже однозначно вычислимо, т.е. допускает однозначную вычислимую нумерацию).
\ { R } вычислимо (даже однозначно вычислимо, т.е. допускает однозначную вычислимую нумерацию).
Замечание: Отмеченное в 2 свойство является нетривиальным.
Справедливо следующее утверждение о семействе П.
Предложение 1. Семейство П обладает счетным семейством попарно неэквивалентных однозначных нумераций.□
Наиболее общими результатами о существовании однозначных вычислимых нумераций являются следующие две теоремы.
Теорема 1. Пусть вычислимое семейство  содержит сильно перечислимое семейство
содержит сильно перечислимое семейство  конечных множеств такое, что
конечных множеств такое, что
а) любое множество из S есть объединение возрастающей последовательности множеств из  ;
;
б) любое множество из  содержится в некотором собственном подмножестве из
содержится в некотором собственном подмножестве из  .
.
Тогда существует однозначная вычислимая нумерация семейства  .□
.□
Введем следующие определения. Множество М предельно для семейства множеств  , если для любого конечного подмножества
, если для любого конечного подмножества 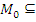 M в
M в  существует М' такое, что
существует М' такое, что  М'. Семейство
М'. Семейство  предельно для семейства
предельно для семейства  , если любое множество из
, если любое множество из  предельно для семейства
предельно для семейства  .
.
Теорема 2. Пусть вычислимое семейство  содержит вычислимое подсемейство
содержит вычислимое подсемейство  такое, что
такое, что
а) если два множества из  имеют непустое пересечение, то одно из них содержится в другом;
имеют непустое пересечение, то одно из них содержится в другом;
б) частично упорядоченное множество <  ,
,  > не имеет максимальных элементов;
> не имеет максимальных элементов;
в) семейство  предельно для семейства
предельно для семейства  .
.
Тогда существует однозначная вычислимая нумерация семейства  .□
.□
Минимальными нумерациями являются также и позитивные (однозначные нумерации, в частности, также позитивны). Сразу следует отметить, что довольно многие семейства  не имеют однозначных нумераций, но имеют позитивные нумерации. Укажем простейший пример.
не имеют однозначных нумераций, но имеют позитивные нумерации. Укажем простейший пример.
Пусть А – рекурсивно перечислимое нерекурсивное множество, полагаем

Нумерацию  определяем так:
определяем так:

Ясно, что  – вычислимая нумерация семейства
– вычислимая нумерация семейства  . Можно заключить, что любая другая вычислимая нумерация семейства
. Можно заключить, что любая другая вычислимая нумерация семейства  эквивалентна
эквивалентна  . Заметим теперь, что
. Заметим теперь, что  – неразрешимая нумерация. Последнее следует из эквивалентности
– неразрешимая нумерация. Последнее следует из эквивалентности  .
.
Замечание. Естественная нумерация слов конечного алфавита определяет некоторую нумерацию свободной полугруппы с образующими из этого алфавита. Эта нумерация слов определяет (порождает) и нумерацию любой конечно определенной полугруппы, причем последняя, всегда будет позитивной.
Существует довольно много достаточных условий существования (хотя бы одной) позитивной нумерации. Приведем для примера следующие предложения.
Предложение 2. Пусть вычислимое семейство  содержит вычислимое семейство
содержит вычислимое семейство  конечных множеств такое, что S предельно для
конечных множеств такое, что S предельно для  , тогда
, тогда  имеет позитивную нумерацию.□
имеет позитивную нумерацию.□
Предложение 3. Если вычислимое семейство  содержит наибольшее по включению множество,
содержит наибольшее по включению множество,  имеет позитивную нумерацию.
имеет позитивную нумерацию.
Отметим, что семейство П имеет счетное множество попарно не эквивалентных позитивных нумераций, не эквивалентных однозначным нумерациям.
У П, а также и у других семейств  может существовать и много минимальных непозитивных нумераций.
может существовать и много минимальных непозитивных нумераций.
|
из
5.00
|
Обсуждение в статье: Предварительные сведения |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

