 |
Главная |
Нумерации множества и его подмножеств
|
из
5.00
|
Пусть  – произвольное непустое не более чем счетное множество. Нумерацией множества
– произвольное непустое не более чем счетное множество. Нумерацией множества  назовем всякое отображение ν множества N всех натуральных чисел на множество
назовем всякое отображение ν множества N всех натуральных чисел на множество  . Пара
. Пара  = (S, ν), где ν – некоторая нумерация множества S, называется нумерованным множеством. Для дальнейшего будет удобно считать, что и пустое множество Ø обладает некоторой единственной «нумерацией» o, а «нумерованное» множество (Ø, o) будем обозначать О.
= (S, ν), где ν – некоторая нумерация множества S, называется нумерованным множеством. Для дальнейшего будет удобно считать, что и пустое множество Ø обладает некоторой единственной «нумерацией» o, а «нумерованное» множество (Ø, o) будем обозначать О.
Пусть  – два подмножества S и
– два подмножества S и  – нумерации множеств
– нумерации множеств  соответственно. Будем говорить,
соответственно. Будем говорить,  сводится к
сводится к  (
(  ), если
), если  = o (и тогда
= o (и тогда  = Ø) или
= Ø) или  o,
o, 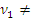 o и существует общерекурсивная функция f такая, что
o и существует общерекурсивная функция f такая, что  x =
x =  f ( x ) для любого
f ( x ) для любого  , короче
, короче  =
=  . Такую функцию будем называть сводящей. Заметим, что из
. Такую функцию будем называть сводящей. Заметим, что из  следует, что
следует, что  . Действительно, если
. Действительно, если  = o, то
= o, то 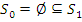 , если же
, если же  o и s
o и s  , то
, то  x = s для некоторого x
x = s для некоторого x  N, но
N, но  x =
x =  f ( x )
f ( x )  . Легко проверяется, что отношение сводимости
. Легко проверяется, что отношение сводимости  является рефлексивным и транзитивным. Если
является рефлексивным и транзитивным. Если 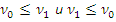 , то нумерации
, то нумерации  и
и  назовем эквивалентными (
назовем эквивалентными (  . Класс всех нумераций, эквивалентных ν, обозначим через [ν].
. Класс всех нумераций, эквивалентных ν, обозначим через [ν].
Если  - нумерация
- нумерация  , s
, s  , n
, n  N и
N и  n = s, то число n называется
n = s, то число n называется  - номером элемента s. Сводимость нумерации
- номером элемента s. Сводимость нумерации  к
к  означает, что по любому
означает, что по любому  - номеру любого элемента из
- номеру любого элемента из  можно эффективно найти некоторый
можно эффективно найти некоторый  - номер этого же элемента.
- номер этого же элемента.
Множество всех нумераций множества S обозначим через H ( S ), а множество всех нумераций подмножества S (включая пустое) обозначим через H *( S ). Определим отображение r множества H * ( S ) на Р( S ) – множество всех подмножеств S – так: r(o) 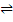 Ø; r(ν)
Ø; r(ν)  ν(N) для ν
ν(N) для ν  o
o  H *( S ). Отметим, что
H *( S ). Отметим, что  для любого подмножества
для любого подмножества  и H *( S ) =
и H *( S ) = 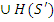 .
.
Множество классов эквивалентных нумераций множества S (подмножеств S) обозначим через L ( S ) (L *( S )). На этих множествах отношение сводимости индуцирует отношение частичного порядка, которое будем обозначать также  . Отображение r: H *( S )
. Отображение r: H *( S )  Р( S ) индуцирует отображение L *( S )
Р( S ) индуцирует отображение L *( S )  Р( S ), которое также будем обозначать через r. Ясно, что r сохраняет отношение порядка (точнее: a
Р( S ), которое также будем обозначать через r. Ясно, что r сохраняет отношение порядка (точнее: a  b
b  L *( S )
L *( S )  r ( a )
r ( a )  . Как и выше
. Как и выше  для
для  .
.
На множестве H *( S ) определим операцию  прямой суммы нумераций.
прямой суммы нумераций.
Пусть  H *( S ); если
H *( S ); если  = o, то
= o, то 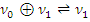 ; если
; если  = o, то
= o, то 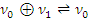 ; пусть
; пусть  o
o  o и
o и  ,
,  , тогда нумерация
, тогда нумерация  множества
множества  определяется так:
определяется так:

Предложение 1. Если  H *( S ), то
H *( S ), то 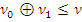 тогда, когда
тогда, когда  .□
.□
Следствие. Частично упорядоченные множества L *( S ) и L ( S ) являются верхними полурешетками, а для операции  точной верхней грани справедливо следующее соотношение: для
точной верхней грани справедливо следующее соотношение: для  H *( S )
H *( S )
[  ]
] 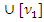 = [
= [  ].□
].□
Заметим, что L ( S )  L *( S ) является коидеалом, т.е. удовлетворяет условию
L *( S ) является коидеалом, т.е. удовлетворяет условию
a  L ( S )
L ( S ) 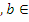 L *( S ), a
L *( S ), a 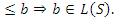
Полезно заметить и то, что r(a  ) =
) =  (
( 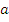 )
)  ) для любых a , b
) для любых a , b  L *( S ).
L *( S ).
Предложение 2. Полурешетка L *( S ) является дистрибутивной полурешеткой с нулем [o].
Нужно доказать, что если 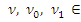 H *( S ) и
H *( S ) и  , то существуют такие
, то существуют такие  H *( S ), что
H *( S ), что 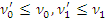 и
и  . Ясно, что если
. Ясно, что если 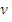 = o, то в качестве
= o, то в качестве  нужно также взять o. Пусть
нужно также взять o. Пусть  o и пусть f
o и пусть f  Ơ – функция, которая сводит
Ơ – функция, которая сводит  к
к  , т.е.
, т.е.  =
=  ) f. Определяем множества
) f. Определяем множества  так:
так:  ,
,  . Множества
. Множества  рекурсивно перечислимы. Если
рекурсивно перечислимы. Если  Ø, то полагаем
Ø, то полагаем 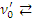 o; если
o; если  Ø, то пусть
Ø, то пусть  Ơ такова, что
Ơ такова, что  ;
;  , и пусть
, и пусть  . Если
. Если  = Ø, то полагаем
= Ø, то полагаем  o; если
o; если  Ø, то пусть
Ø, то пусть  Ơ такова, что
Ơ такова, что 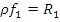 ;
;  , и пусть
, и пусть  . Из определения видно, что
. Из определения видно, что  . Поэтому достаточно показать, что
. Поэтому достаточно показать, что  . Рассмотрим случай
. Рассмотрим случай 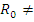 Ø и
Ø и  Ø (другие случаи проще). Пусть
Ø (другие случаи проще). Пусть  таковы, что
таковы, что  и
и  для
для  ;
;  и
и  для
для  . Определим функцию
. Определим функцию  так:
так:

 – общерекурсивная функция. Проверим, что
– общерекурсивная функция. Проверим, что  = (
= (  )
) 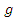 . Пусть x таково, что f ( x ) четно, тогда
. Пусть x таково, что f ( x ) четно, тогда
 = (
= (  )
)  (
( 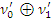 ) (2
) (2  (
( 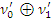 )
)  .
.
Пусть х таково, что f ( x ) нечетно, тогда
 = (
= (  )
)  (
( 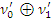 ) (2
) (2  (
(  )
)  .
.
Итак,  = (
= (  )
) 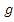 и
и  . Покажем теперь, что
. Покажем теперь, что  и
и  . Пусть
. Пусть  , тогда
, тогда
 ) f
) f 
 ) f
) f  .
.
Следовательно,  , (
, (  )
)  и
и  .□
.□
Следствие. Если a  L *( S ) (L ( S )), то полурешетка
L *( S ) (L ( S )), то полурешетка  является дистрибутивной полурешеткой.□
является дистрибутивной полурешеткой.□
Сводимость нумераций довольно близка понятию m – сводимости. Сейчас укажем простейшую связь.
Предложение 3. Если  H *( S ),
H *( S ),  ,
,  - нумерация множества
- нумерация множества  , то
, то  для любого
для любого  .
.
Действительно, если f  Ơ – сводящая функция, т.е.
Ơ – сводящая функция, т.е.  =
=  , то легко видеть, что функция f m – сводит
, то легко видеть, что функция f m – сводит  .□
.□
Необходимое условие сводимости нумераций, указанное в этом предложении, конечно, не является достаточным, однако существует частный случай, когда это так.
Рассмотрим пример, когда  . Для любого собственного подмножества М множества N определим нумерацию
. Для любого собственного подмножества М множества N определим нумерацию 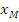 множества S так:
множества S так:

Нумерация 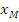 является просто характеристической функцией множества М. Нумерованное множество ({0,1},
является просто характеристической функцией множества М. Нумерованное множество ({0,1},  ) будем обозначать
) будем обозначать  .
.
Нетрудно проверить, что для 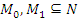 имеем
имеем  тогда и только тогда, когда
тогда и только тогда, когда  . Отсюда вытекает следующее
. Отсюда вытекает следующее
Предложение 4. Верхняя полурешетка L({0,1}) классов эквивалентных нумераций множества {0,1} изоморфна верхней полурешетке  всех m – степеней собственных подмножеств N.□
всех m – степеней собственных подмножеств N.□
Следствие. Полурешетка классов эквивалентных нумераций двухэлементного множества имеет мощность континуума.
Действительно, собственных подмножеств N континуум, а каждая m – степень состоит не более чем из счетного семейства множеств.□
Отметим, что если S одноэлементно, то S имеет только одну нумерацию и, следовательно, в этом случае L ( S ) одноэлементна.
Если  , то, очевидно, H *(
, то, очевидно, H *(  )
)  H *(
H *(  ), L *(
), L *(  )
)  L *(
L *(  ) и L *(
) и L *( 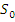 ) является идеалом полурешетки L *(
) является идеалом полурешетки L *(  ). Можно ли так же естественно вложить L(
). Можно ли так же естественно вложить L( 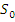 ) в L(
) в L(  )? Ответ, вообще говоря, будет отрицательным в смысле «естественности», но некоторые изоморфные вложения L(
)? Ответ, вообще говоря, будет отрицательным в смысле «естественности», но некоторые изоморфные вложения L(  ) в L(
) в L(  ) в качестве идеала будут построены. Конечно, нетривиальным случаем является только случай, когда
) в качестве идеала будут построены. Конечно, нетривиальным случаем является только случай, когда  – собственное подмножество
– собственное подмножество  .
.
Предложение 5. Пусть  – собственное подмножество
– собственное подмножество  , а – минимальный элемент в L(
, а – минимальный элемент в L(  \
\  ), тогда отображение
), тогда отображение  для b
для b 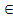 L(
L( 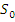 ) (операция
) (операция  определена в L *(
определена в L *(  )
)  L(
L(  )
) 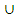 L(
L(  \
\  )) есть изоморфное отображение L(
)) есть изоморфное отображение L( 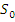 ) на некоторый идеал L(
) на некоторый идеал L(  ).
).
Ясно, что  - гомоморфизм полурешетки L(
- гомоморфизм полурешетки L(  ) в полурешетку L(
) в полурешетку L(  ). Покажем, что
). Покажем, что  - изоморфизм. Для этого достаточно проверить, что если
- изоморфизм. Для этого достаточно проверить, что если  для
для  (
(  ). Пусть
). Пусть  и
и  (
( 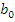 )=
)=  . Из последнего следует, что
. Из последнего следует, что  . Так как L *(
. Так как L *(  ) – дистрибутивная полурешетка, то существуют c и d такие, что
) – дистрибутивная полурешетка, то существуют c и d такие, что 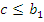 ,
,  и
и 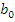 =
=  . Так как
. Так как  , то
, то  ) =
) = 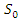 ; а так как
; а так как  , то
, то  ) =
) =  \
\  . Следовательно,
. Следовательно, 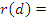 Ø,
Ø,  = o и
= o и 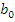 =
=  . Получаем противоречие. Итак,
. Получаем противоречие. Итак,  - изоморфизм. Пусть b
- изоморфизм. Пусть b 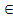 L(
L(  ), c
), c  L(
L(  ) и c
) и c  ; тогда существуют
; тогда существуют  такие, что
такие, что  и
и  . Так как
. Так как  , а
, а  , то
, то  \
\  . Но
. Но 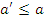 и
и  \
\  . Следовательно,
. Следовательно, 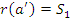 \
\ 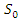 и
и  L(
L(  \
\ 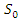 ). Но так как а – минимальный элемент L(
). Но так как а – минимальный элемент L(  \
\  ) и
) и 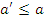 , то
, то  . Покажем теперь, что
. Покажем теперь, что  L(
L(  ). Для этого достаточно показать, что
). Для этого достаточно показать, что  . Включение
. Включение  уже показано; из того, что
уже показано; из того, что  \
\  , а
, а  , следует, что
, следует, что  \
\  \
\ 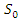 ) =
) = 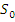 . Следовательно,
. Следовательно,  =
=  ,
,  L(
L(  ). Из
). Из  следует, что
следует, что 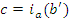 и
и  L(
L(  ). Таким образом,
). Таким образом,  L(
L(  )) – идеал L(
)) – идеал L(  ).□
).□
Для того чтобы применять предложение 5 для решения вопроса о вложении L(  ) в L(
) в L( 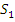 ), нужно выяснить вопрос о существовании минимальных элементов в полурешетках L(S).
), нужно выяснить вопрос о существовании минимальных элементов в полурешетках L(S).
Предложение 6. Если S конечно, то L(S) имеет наименьший элемент и является дистрибутивной полурешеткой.
Пусть  и
и  . Определим нумерацию
. Определим нумерацию  этого множества так:
этого множества так:  , если m < n, и
, если m < n, и  , если
, если  . Пусть
. Пусть  – произвольная нумерация S и
– произвольная нумерация S и  – некоторые
– некоторые  – номера элементов
– номера элементов  соответственно. Определяя функцию f так, что f(i)
соответственно. Определяя функцию f так, что f(i)  для i < n и f(i)
для i < n и f(i)  для
для 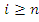 , получаем
, получаем  и f
и f  Ơ. Следовательно,
Ơ. Следовательно,  и [
и [  ] – наименьший элемент L(S).□
] – наименьший элемент L(S).□
Следствие. Если S – конечное множество, содержащее, по крайней мере, два элемента, то полурешетка L(S) континуальна.□
Предложение 6 показывает, что «естественное» вложение L(  ) в L(
) в L( 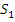 ) (для
) (для  ) существует, когда
) существует, когда 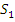 \
\ 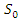 конечно.
конечно.
В случае бесконечного S полурешетка L(S) не имеет наименьшего элемента, но имеет много минимальных. Для установления этого напомним следующее определение. Нумерация 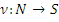 множества S называется однозначной, если ν n ≠ ν m для любых n ≠ m
множества S называется однозначной, если ν n ≠ ν m для любых n ≠ m  N.
N.
Предложение 7. Если S – счетное множество, то существует точно континуум попарно не эквивалентных и даже попарно несравнимых однозначных нумераций множества S.
Пусть  – группа всех перестановок множества N,
– группа всех перестановок множества N,  - подгруппа общерекурсивных перестановок N. Хорошо известно, что
- подгруппа общерекурсивных перестановок N. Хорошо известно, что  счетна, а
счетна, а  имеет мощность континуума, отсюда следует, что множество левых смежных классов
имеет мощность континуума, отсюда следует, что множество левых смежных классов  также имеет мощность континуума. Пусть
также имеет мощность континуума. Пусть  – некоторая фиксированная однозначная нумерация множества S. Тогда любая другая однозначная нумерация
– некоторая фиксированная однозначная нумерация множества S. Тогда любая другая однозначная нумерация  может быть однозначно представлена в виде
может быть однозначно представлена в виде  , а класс нумераций, эквивалентных нумерации
, а класс нумераций, эквивалентных нумерации  , состоит из всех нумераций вида
, состоит из всех нумераций вида  , так что существует взаимно однозначное соответствие между классами эквивалентных однозначных нумераций множества S и смежными классами из
, так что существует взаимно однозначное соответствие между классами эквивалентных однозначных нумераций множества S и смежными классами из 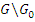 . Так как неэквивалентные однозначные нумерации, очевидно, не сравнимы, то отсюда и следует заключение предложения.□
. Так как неэквивалентные однозначные нумерации, очевидно, не сравнимы, то отсюда и следует заключение предложения.□
Следствие 1. Если S – счетное множество, L(S) имеет континуум минимальных нумераций.
Следствие 2. Если S – не более чем счетное множество, содержащее, по крайней мере, два элемента, L(S) имеет идеал, изоморфный полурешетке  всех m – степеней собственных подмножеств N.
всех m – степеней собственных подмножеств N.
Это вытекает из предложения 5 и следствия 1.
Обратимся теперь к вопросу об изоморфизме полурешеток L(S),  и L(
и L( 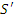 ), L *(
), L *(  ) для двух не более чем счетных множеств S и
) для двух не более чем счетных множеств S и  . Ясно, что если S и
. Ясно, что если S и 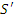 равномощны, то эти полурешетки соответственно изоморфны. Если S конечно, а
равномощны, то эти полурешетки соответственно изоморфны. Если S конечно, а 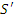 бесконечно, то L(S) имеет наименьший элемент, а L(
бесконечно, то L(S) имеет наименьший элемент, а L(  ) наименьшего элемента не имеет, следовательно, в этом случае L(S) и L(
) наименьшего элемента не имеет, следовательно, в этом случае L(S) и L(  ) не изоморфны. Полурешетка
) не изоморфны. Полурешетка  имеет наименьший элемент. Рассмотрим, какие же минимальные (отличные от [o]) элементы она имеет. Каждому элементу s
имеет наименьший элемент. Рассмотрим, какие же минимальные (отличные от [o]) элементы она имеет. Каждому элементу s  соответствует одноэлементное множество L({s})
соответствует одноэлементное множество L({s}) 
 . Нетрудно проверить, что соответствующий элемент
. Нетрудно проверить, что соответствующий элемент  будет минимальным, этот элемент будем обозначать
будет минимальным, этот элемент будем обозначать  . Пусть a – произвольный отличный от нуля элемент
. Пусть a – произвольный отличный от нуля элемент  , тогда r(a)
, тогда r(a)  Ø. Пусть s
Ø. Пусть s  r(a), тогда легко проверяется, что
r(a), тогда легко проверяется, что 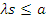 . Проведенные рассмотрения доказывают следующее
. Проведенные рассмотрения доказывают следующее
Предложение 8. Отображение  устанавливает взаимно однозначное соответствие между элементами S и минимальными элементами
устанавливает взаимно однозначное соответствие между элементами S и минимальными элементами  .
.
Следствие. 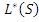 и L *(
и L *(  ) изоморфны тогда и только тогда, когда
) изоморфны тогда и только тогда, когда  и
и 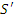 равномощны.
равномощны.
Итак, неясным остается только вопрос, изоморфны ли полурешетки  и L(
и L( 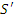 ) для конечных множеств
) для конечных множеств  и
и  , имеющих не менее двух элементов. Оказывается, что полурешетка
, имеющих не менее двух элементов. Оказывается, что полурешетка  для конечных
для конечных  , имеющих, по крайней мере, два элемента, обладает замечательным свойством универсальности, которое в качестве следствия влечет изоморфизм всех таких полурешеток. Переходим к точной формулировке этого результата.
, имеющих, по крайней мере, два элемента, обладает замечательным свойством универсальности, которое в качестве следствия влечет изоморфизм всех таких полурешеток. Переходим к точной формулировке этого результата.
Дистрибутивную полурешетку L назовем допустимой, если она имеет нуль и если всякий главный идеал L не более чем счетен. Заметим, что если 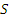 конечно, то
конечно, то  – допустимая полурешетка.
– допустимая полурешетка.
Теорема 1. Пусть  – конечное множество, имеющее, по крайней мере, два элемента; пусть L – допустимая полурешетка мощности меньше континуума,
– конечное множество, имеющее, по крайней мере, два элемента; пусть L – допустимая полурешетка мощности меньше континуума,  – идеал L и
– идеал L и 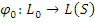 – изоморфное вложение
– изоморфное вложение 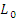 на идеал
на идеал  , тогда существует изоморфное вложение
, тогда существует изоморфное вложение 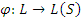 на идеал
на идеал  , которое продолжает
, которое продолжает  (т.е.
(т.е. 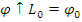 ).
).
Следствие 1. Если  и
и  – конечные множества, имеющие, по крайней мере, два элемента, то полурешетки
– конечные множества, имеющие, по крайней мере, два элемента, то полурешетки  и L(
и L(  ) изоморфны.
) изоморфны.
Следствие 2. Если  – конечное множество, имеющее, по крайней мере, два элемента, то полурешетка
– конечное множество, имеющее, по крайней мере, два элемента, то полурешетка  изоморфна полурешетке
изоморфна полурешетке  всех m – степеней собственных подмножеств N.
всех m – степеней собственных подмножеств N.
Следствие 3. Если  , то полурешетка
, то полурешетка  и
и  изоморфны.
изоморфны.
Это также нетрудное следствие свойства универсальности, указанного в теореме.
Перейдем теперь к изучению более тонкого отношения сводимости между нумерациями. Пусть  – непустые подмножества
– непустые подмножества  ,
,  1 – сводится к
1 – сводится к  (
(  ), если существует одно – однозначная общерекурсивная функция f (1 – сводящая функция) такая, что
), если существует одно – однозначная общерекурсивная функция f (1 – сводящая функция) такая, что  =
=  . Класс всех одноместных одно – однозначных общерекурсивных функций обозначим
. Класс всех одноместных одно – однозначных общерекурсивных функций обозначим 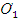 . Нумерации
. Нумерации  назовем изоморфными (
назовем изоморфными (  ), если существует общерекурсивная перестановка f (т.е.
), если существует общерекурсивная перестановка f (т.е.  и
и  ) такая, что
) такая, что 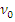 =
=  . Отношение
. Отношение  является транзитивным, а отношение
является транзитивным, а отношение  является отношением эквивалентности.
является отношением эквивалентности.
Теорема 2. Пусть  – две нумерации множества
– две нумерации множества  . Если
. Если  и
и  , то
, то  .
.
Пусть  и 1 – сводят
и 1 – сводят  и
и 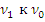 соответственно, т.е.
соответственно, т.е.  =
=  и
и  =
=  . Определим теперь функции
. Определим теперь функции  следующим образом:
следующим образом:


Имеем  и
и  .
.
Положим  ,
,  . Заметим, что для любого
. Заметим, что для любого 

Лемма 1. Если  – конечное множество, то и
– конечное множество, то и  – конечное множество, имеющее то же число элементов, и нао
– конечное множество, имеющее то же число элементов, и нао
|
из
5.00
|
Обсуждение в статье: Нумерации множества и его подмножеств |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

