 |
Главная |
Категория нумерованных множеств и ее свойства
|
из
5.00
|
В предыдущем параграфе изучались нумерации подмножеств некоторого множества и отношение сводимости между нумерациями. Обратимся теперь к «взаимодействию» произвольных нумерованных множеств. Наиболее естественным путем для такого изучения является соответствующей категории – категории  нумерованных множеств.
нумерованных множеств.
Перейдем к точным определениям. Объектами категории 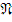 являются все нумерованные множества, включая «пустое» нумерованное множество О. Если
являются все нумерованные множества, включая «пустое» нумерованное множество О. Если  – произвольное нумерованное множество, то существует и притом единственный морфизм o из О в
– произвольное нумерованное множество, то существует и притом единственный морфизм o из О в  . Если
. Если  = (
= (  ,
,  ) и
) и  = (
= (  ,
,  ) – произвольные не пустые нумерованные множества, то морфизмом из
) – произвольные не пустые нумерованные множества, то морфизмом из 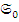 в
в 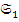 назовем всякое отображение
назовем всякое отображение  , для которого существует функция
, для которого существует функция 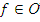 такая, что
такая, что  , иными словами, если диаграмма
, иными словами, если диаграмма
 f
f

 N N
N N
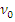

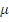


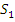
коммутативна. То, что 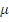 – морфизм из
– морфизм из  в
в  , будет обозначаться так:
, будет обозначаться так: 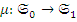 . Множество всех морфизмов из
. Множество всех морфизмов из 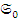 в
в 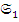 обозначим через Mor (
обозначим через Mor ( 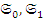 ). Композиция морфизмов определяется естественным образом. Объект О является нулевым объектом категории
). Композиция морфизмов определяется естественным образом. Объект О является нулевым объектом категории  .
.
Отметим следующие простые свойства морфизмов.
1. Если  = (
= (  ,
, 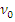 ) и
) и  = (
= (  ,
,  ),
),  –
–  – вполне перечислимое множество, а
– вполне перечислимое множество, а 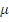 – морфизм из
– морфизм из  в
в  , то
, то 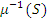 –
–  – вполне перечислимое подмножество
– вполне перечислимое подмножество  .
.
Действительно, пусть 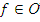 такова, что
такова, что  . Тогда
. Тогда  . Таким образом, f m – сводит
. Таким образом, f m – сводит  к рекурсивно перечислимому множеству
к рекурсивно перечислимому множеству  , следовательно,
, следовательно,  будет
будет  – вполне перечислимым.
– вполне перечислимым.
2. Если 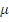 – морфизм из
– морфизм из  = (
= (  ,
, 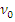 ) в
) в  = (
= (  ,
,  ), то
), то  сохраняет предпорядки, определенные нумерациями, т.е.
сохраняет предпорядки, определенные нумерациями, т.е. 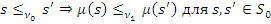 .
.
Следует из 1.
3. Если 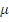 – морфизм из
– морфизм из 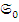 = (
= (  ,
, 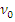 ) в
) в  = (
= (  ,
,  ), то
), то 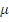 – непрерывное отображение топологического пространства (
– непрерывное отображение топологического пространства (  ,
, 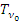 ) в топологическое пространство (
) в топологическое пространство (  ,
,  ).
).
Следует из 1.
Еще несколько определений. Через N, будем обозначать нумерованное множество (N,  ). Для любого множества
). Для любого множества  через Э (
через Э (  ) обозначим множество всех отношений эквивалентности на множестве
) обозначим множество всех отношений эквивалентности на множестве  . Это множество относительно естественного отношения включения является полной решеткой; если
. Это множество относительно естественного отношения включения является полной решеткой; если 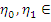 Э (
Э (  ), то
), то 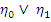 и
и  обозначают точную верхнюю и соответственно нижнюю грань элементов
обозначают точную верхнюю и соответственно нижнюю грань элементов 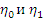 . Для
. Для  Э (
Э (  ), через
), через  обозначим нумерованное множество (
обозначим нумерованное множество (  – операция
– операция  – замыкания ([
– замыкания ([  для
для  Э (
Э (  ). Более общо, если
). Более общо, если  = (
= (  ,
,  ) – нумерованное множество,
) – нумерованное множество,  Э (
Э (  , то
, то  – это нумерованное множество (
– это нумерованное множество (  ); отображение
); отображение  является, очевидно, морфизмом из
является, очевидно, морфизмом из  в
в 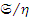 .
.
Предложение 1. Категория  эквивалентна своей полной подкатегории
эквивалентна своей полной подкатегории 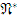 , определенной семейством объектов {O}
, определенной семейством объектов {O}  .
.
По определению эквивалентности категорий  и
и  означает, что существует два ковариантных функтора
означает, что существует два ковариантных функтора  и
и  таких, что функторы
таких, что функторы 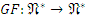 и
и  эквивалентны тождественным функторам
эквивалентны тождественным функторам  и
и  соответственно. В качестве функтора F возьмем функтор
соответственно. В качестве функтора F возьмем функтор  вложения категории
вложения категории 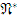 как подкатегории
как подкатегории  . Функтор
. Функтор  определим так:
определим так:  ; если
; если  = (
= (  ,
,  )
)  , то
, то 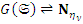 , для простоты вместо
, для простоты вместо  будем просто писать
будем просто писать 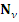 , где
, где  – нумерационная эквивалентность нумерации
– нумерационная эквивалентность нумерации  . Существует естественный морфизм
. Существует естественный морфизм 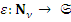 , определенный так:
, определенный так: 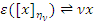 для
для  . Легко проверить, что это определение корректно и что
. Легко проверить, что это определение корректно и что  – морфизм. На самом деле
– морфизм. На самом деле  является эквивалентностью категории
является эквивалентностью категории  , т.е. существует такой морфизм
, т.е. существует такой морфизм  , что
, что  =
=  , а
, а  =
= 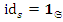 . Действительно, отображение
. Действительно, отображение  определим так:
определим так:  . Ясно, что
. Ясно, что  – морфизм, обладающий нужными свойствами. Продолжим определение функтора
– морфизм, обладающий нужными свойствами. Продолжим определение функтора  . Пусть
. Пусть  = (
= (  ,
, 
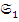 = (
= (  ,
,  ) и
) и  такова, что
такова, что 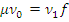 ; определяем
; определяем  так:
так: 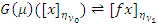 для
для  . Это определение корректно, так как если
. Это определение корректно, так как если  , то
, то  ,
,  , т.е.
, т.е.  . Ясно также, что
. Ясно также, что  – морфизм из
– морфизм из  в
в  . Так определенное отображение
. Так определенное отображение  является функтором. Для проверки того, что функтор
является функтором. Для проверки того, что функтор  эквивалентен тождественному функтору, нужно построить единственное преобразование
эквивалентен тождественному функтору, нужно построить единственное преобразование  такое, что все морфизмы
такое, что все морфизмы  являются эквивалентностями категории
являются эквивалентностями категории  . В качестве таких
. В качестве таких  нужно взять построенные выше морфизмы
нужно взять построенные выше морфизмы  .
.
Следствие. Категория  эквивалентна малой категории, т.е. категории, семейство объектов которой образует множество.
эквивалентна малой категории, т.е. категории, семейство объектов которой образует множество.
Простая проверка показывает, что для того чтобы морфизм 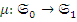 был мономорфизмом (эпиморфизмом) категории
был мономорфизмом (эпиморфизмом) категории  , необходимо и достаточно, чтобы отображение
, необходимо и достаточно, чтобы отображение  , задающее морфизм, было одно – однозначным (отображением на
, задающее морфизм, было одно – однозначным (отображением на 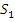 ). Для всякого морфизма
). Для всякого морфизма  o
o  через
через  обозначим отношение эквивалентности на
обозначим отношение эквивалентности на  , определенное так:
, определенное так:  . Вместо обозначения
. Вместо обозначения  будем использовать в этом случае обозначение
будем использовать в этом случае обозначение  , а естественный морфизм из
, а естественный морфизм из  в
в  будем обозначать
будем обозначать  . Определим морфизм
. Определим морфизм  такой, чтобы диаграмма
такой, чтобы диаграмма
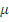



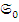
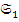


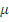

была коммуникативной. Пусть  , тогда положим
, тогда положим  . Проверим корректность определения
. Проверим корректность определения  ; пусть
; пусть 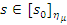 , тогда
, тогда 
 . Если
. Если  такова, что
такова, что 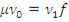 , то
, то  , так что
, так что  – морфизм. Соотношение
– морфизм. Соотношение  очевидно. Представление всякого морфизма
очевидно. Представление всякого морфизма 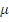 в виде
в виде  , где
, где  однозначно определены указанным выше способом, назовем каноническим представлением морфизма
однозначно определены указанным выше способом, назовем каноническим представлением морфизма 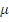 . Отметим следующие свойства канонического представления:
. Отметим следующие свойства канонического представления: 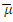 – эпиморфизм, а
– эпиморфизм, а  – мономорфизм. Однако этими двумя свойствами представления оно не определяется однозначно (с точностью до разумной теоретико – категорной эквивалентности). Для того чтобы теоретико – категорно охарактеризовать каноническое представление, введем понятие факторизации. Морфизм
– мономорфизм. Однако этими двумя свойствами представления оно не определяется однозначно (с точностью до разумной теоретико – категорной эквивалентности). Для того чтобы теоретико – категорно охарактеризовать каноническое представление, введем понятие факторизации. Морфизм  факторизацией, если для любого морфизма
факторизацией, если для любого морфизма  такого, что
такого, что 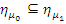 , существует единственный морфизм
, существует единственный морфизм 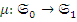 такой, что диаграмма
такой, что диаграмма



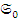
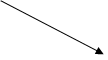

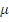
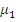
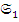
Лемма. Если диаграмма коммутативна.


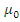



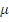
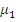
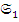
коммутативна и  и
и 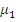 или
или  и
и 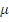 – факторизации, то все эти морфизмы – факторизации.□
– факторизации, то все эти морфизмы – факторизации.□
Предложение 2. Пусть следующая диаграмма:





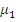





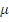
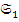



(без  ) коммутативна;
) коммутативна;  – каноническое представление,
– каноническое представление,  – факторизация,
– факторизация, 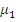 – мономорфизм. Тогда существует морфизм
– мономорфизм. Тогда существует морфизм  такой, что
такой, что  – эквивалентность категории
– эквивалентность категории  и диаграмма, приведенная выше, коммутативна.
и диаграмма, приведенная выше, коммутативна.
Из равенства  и мономорфности
и мономорфности 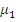 следует, что
следует, что 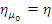 , тогда существование морфизма
, тогда существование морфизма  и морфизма
и морфизма  таких, что диаграммы
таких, что диаграммы


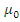





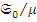





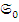
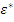

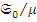
коммутативны, вытекает из того, что  и
и  – факторизации. Из единственности таких морфизмов вытекает, что
– факторизации. Из единственности таких морфизмов вытекает, что  ,
,  . Таким образом,
. Таким образом,  – эквивалентность категории
– эквивалентность категории  . Для проверки коммутативности большой диаграммы достаточно показать только, что
. Для проверки коммутативности большой диаграммы достаточно показать только, что 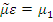 . Обозначая
. Обозначая  , получим
, получим  . Но так как
. Но так как  – факторизация, то может существовать только один морфизм
– факторизация, то может существовать только один морфизм 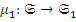 такой, что
такой, что 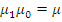 ; поэтому
; поэтому  .
.
Предложение 2 и показывает нужную «единственность» канонического представления. Впредь под каноническим представлением морфизма  будем понимать всякое представление его в виде
будем понимать всякое представление его в виде 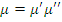 , где
, где  – факторизация, а
– факторизация, а  – мономорфизм.
– мономорфизм.
Для того чтобы понять, что факторизация может быть определена в чисто теоретико – категорных терминах (для этого достаточно такое определение для  ), определим объект 1 категории
), определим объект 1 категории  как множество {0}, снабженное единственно возможной нумерацией. Укажем следующие простые свойства:
как множество {0}, снабженное единственно возможной нумерацией. Укажем следующие простые свойства:
1. Для любого нумерованного множества  = (
= ( 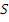 ,
,  ) существует естественное взаимно однозначное соответствие между множеством
) существует естественное взаимно однозначное соответствие между множеством  и множеством Mor (
и множеством Mor (  ).
).
Это соответствие задается отображением  множества Mor (
множества Mor (  ) в
) в  .
.
2. Если 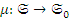 , а
, а 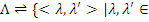 Mor (
Mor (  , то
, то 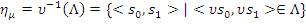 .
.
Легко проверяется.
3. Если  ,
,  , то
, то  .
.
Если  и
и 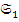 – нумерованные множества и существует эквивалентность
– нумерованные множества и существует эквивалентность  , то
, то  и
и  назовем эквивалентными и будем обозначать это так
назовем эквивалентными и будем обозначать это так  . Отметим, например, что все одноэлементные нумерованные множества эквивалентны
. Отметим, например, что все одноэлементные нумерованные множества эквивалентны 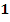 .
.
Если  ,
, 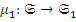 – два морфизма, то назовем (
– два морфизма, то назовем (  и (
и ( 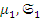 ) эквивалентными над
) эквивалентными над  (менее точно назовем
(менее точно назовем  и
и  эквивалентными над
эквивалентными над  ), если существует эквивалентность
), если существует эквивалентность  такая, что диаграмма
такая, что диаграмма



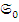



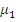

коммутативна.
Фактор – объектом  назовем класс Ф всех пар (
назовем класс Ф всех пар (  ,
, 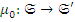 , эквивалентных некоторой паре вида (
, эквивалентных некоторой паре вида ( 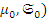 , где
, где  – факторизация. Иногда будем использовать менее точную терминологию, называя фактор – объектом
– факторизация. Иногда будем использовать менее точную терминологию, называя фактор – объектом  пару (
пару (  , где
, где  – факторизация, или даже просто нумерованное множество
– факторизация, или даже просто нумерованное множество  . Заметим, что в каждом классе пар Ф, являющихся фактор – объектом, существует канонический представитель, а именно, если (
. Заметим, что в каждом классе пар Ф, являющихся фактор – объектом, существует канонический представитель, а именно, если (  , то и (
, то и (  , где
, где  – факторизация из канонического представления
– факторизация из канонического представления 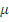 . Пара такого вида (
. Пара такого вида ( 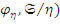 в каждом фактор – объекте существует и единственна. Отсюда следует, что у каждого нумерованного множества существует не более континуума различных фактор – объектов. Обозначим множество всех фактор – объектов
в каждом фактор – объекте существует и единственна. Отсюда следует, что у каждого нумерованного множества существует не более континуума различных фактор – объектов. Обозначим множество всех фактор – объектов  через
через  ; если в этом множестве ввести отношение частичного порядка, полагая для
; если в этом множестве ввести отношение частичного порядка, полагая для 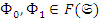
 для (
для (  , (
, (  существует морфизм
существует морфизм  такой, что диаграмма
такой, что диаграмма



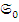



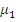
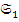
коммутативна, то <  изоморфно полной решетке < Э (
изоморфно полной решетке < Э (  . Это легко следует из рассмотрения канонических представителей в каждом фактор – объекте.
. Это легко следует из рассмотрения канонических представителей в каждом фактор – объекте.
Заметим, что (используя неточную терминологию) любое нумерованное множество 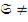 О есть фактор – объект
О есть фактор – объект  . Действительно, если
. Действительно, если  = (
= (  ,
,  ), то, как легко проверить, морфизм
), то, как легко проверить, морфизм  есть факторизация.
есть факторизация.
Замечание. Данное здесь определение фактор – объекта является не совсем обычным, так как в теории категорий фактор – объектом (в неточной терминологии) называют всякий эпиморфный образ. Здесь же мы ограничились образами факторизаций.
Подобъектом  назовем всякую пару (
назовем всякую пару (  ), где
), где  – мономорфизм. (Более точное определение: подобъектом назовем класс Ф всех таких пар (
– мономорфизм. (Более точное определение: подобъектом назовем класс Ф всех таких пар (  ), что (
), что (  ) и (
) и ( 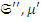 ) эквивалентны в
) эквивалентны в  ; последнее означает существование эквивалентности
; последнее означает существование эквивалентности  такой, что
такой, что  .) Если
.) Если 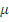 – мономорфизм и эпиморфизм одновременно, то (
– мономорфизм и эпиморфизм одновременно, то (  ) назовем плотным подобъектом
) назовем плотным подобъектом  .
.
Каноническое представление морфизма показывает, что всякий эпиоморфный образ  имеет плотный подобъект, который есть фактор – объект
имеет плотный подобъект, который есть фактор – объект  .
.
Отметим еще, что морфизм является эквивалентностью в  тогда и только тогда, когда он является факторизацией и мономорфизмом.
тогда и только тогда, когда он является факторизацией и мономорфизмом.
Обратимся теперь к вопросам полноты категории  , т.е. к вопросам замкнутости
, т.е. к вопросам замкнутости  относительно различных категорных конструкций.
относительно различных категорных конструкций.
Прямой суммой двух объектов  и
и  категории
категории  называется объект
называется объект  и два морфизма
и два морфизма  и
и  такие, что для любых морфизмов
такие, что для любых морфизмов  , где
, где  – произвольный объект, существует единственный морфизм
– произвольный объект, существует единственный морфизм  такой, что
такой, что 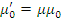 и
и  .
.












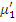

Обозначать прямую сумму будем так: (  ) или (
) или (  ). Тот единственный морфизм
). Тот единственный морфизм  , существование которого (для данных
, существование которого (для данных  и
и 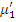 ) утверждается в определении, будем обозначать
) утверждается в определении, будем обозначать  .
.
Предложение 3. В категории 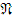 для любых двух объектов
для любых двух объектов 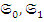 существует их прямая сумма.
существует их прямая сумма.
Если  О, то в качестве
О, то в качестве 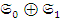 (с естественными морфизмами из
(с естественными морфизмами из  ) можно взять
) можно взять  . Аналогично в случае
. Аналогично в случае  О. Пусть
О. Пусть 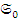 = (
= (  ,
, 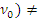 О и
О и  = (
= (  ,
,  О. рассмотрим сначала случай
О. рассмотрим сначала случай  . Полагаем
. Полагаем 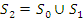 и
и 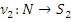 так:
так: 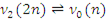 ;
;  . Тогда
. Тогда  (
( 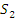 ,
,  – нумерованное множество, а тождественные вложения
– нумерованное множество, а тождественные вложения  и
и  являются морфизмами
являются морфизмами  в
в  . Покажем, что (
. Покажем, что (  ) есть прямая сумма
) есть прямая сумма  . Пусть
. Пусть  = (
= (  ,
,


