Триангуляции Делоне с ограничениями

Триангуляцией Делоне с ограничениями в виде поверхностей называют такую сетку, для которой внутрь сферы, описанной вокруг любого тетраэдра этой сетки, не попадают никакие другие видимые вершинам этого тетраэдра узлы сетки (считается, что точка а видима точке b (и наоборот), если отрезок [a,b] не пересекает никаких поверхностей ограничений). Что такое триангуляция Делоне с ограничениями, если ограничения представлены в том числе и отрезками, до сих пор общепринятого определения нет. 

В двумерном случае проблема построения триангуляции Делоне с ограничениями давно и успешно решена, причем самыми разными способами [3]. Что касается трех измерений, то к настоящему времени разработано лишь несколько алгоритмов, и все они базируются на одном и том же принципе. Их идея заключается в том, чтобы сначала в заданной области построить триангуляцию Делоне без ограничений, а затем восстановить поверхности и линии ограничений путем локальной перестройки сетки. Различие между алгоритмами состоит как раз в том, как именно осуществляется эта перестройка [5, 6, 24, 25].

Рассмотрим один из вариантов такого алгоритма, основанный на идее
К. Хэзлвуд (Carol Hazlewood). В своей работе [21] она доказала, что возможно построить триангуляцию Делоне с ограничениями, ретриангулируя (только) те тетраэдры, которые пересекаются поверхностями ограничений. В статье Хэзлвуд этот факт доказывается для случая пересечения тетраэдра произвольным выпуклым многогранником. Для ясности упростим алгоритм, введя дополнительные несложные требования к входным данным. А именно, потребуем, чтобы поверхности ограничения были представлены либо плоскостями, либо слабо изогнутыми (радиус кривизны много больше линейных размеров элементов) сплайнами, а также, чтобы все угловые точки поверхностей ограничения использовались на первом этапе для построения триангуляции Делоне. В результате все тетраэдры построенной триангуляции могут пересекаться только либо "ребрами" поверхностей ограничений, либо самими поверхностями. Поскольку вариантов таких пересечений немного, для каждого из них можно использовать заранее подготовленный шаблон ретриангуляции. Процесс можно упростить еще больше, если предварительно добиться, чтобы все ребра ограничений были аппроксимированы цепочкой ребер триангуляции. Тогда тетраэдры смогут быть пересечены только плоскостями (сплайнами), а возможных вариантов такого пересечения всего ТРИ (рис. 9).

Таким образом, алгоритм можно разбить на четыре этапа:

1) построение триангуляции Делоне без ограничений;

2) восстановление "ребер" ограничений ("edge recovery");

3) восстановление поверхностей ограничений ("face recovery");

4) отсечение "лишних" тетраэдров, оказавшихся вне границы заданной области ("trimming").

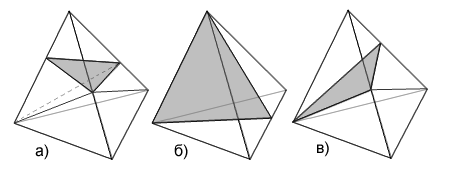
Рис. 9. Три возможных варианта пересечения тетраэдра плоскостью и соответствующие способы разбиения образующихся частей на тетраэдры: а) плоскость не пересекает вершины; б) плоскость пересекает две вершины; в) плоскость пересекает только одну вершину.

Подробнее остановимся на каждом этапе.

Этап 1. Несмотря на кажущуюся простоту, этот этап имеет несколько важных нюансов. Во-первых, как уже было сказано, все "углы" поверхностей ограничения (включая концы "незакрепленных" "ребер"), должны в обязательном порядке войти в набор узлов, по которым строится триангуляция. Во-вторых, поскольку многогранник, получающийся при использовании описанного выше алгоритма, не обязательно будет выпуклым, вполне возможна ситуация, при которой некоторые участки поверхностей ограничений окажутся вне этого многогранника. Чтобы не допустить этого, можно использовать слой дополнительных узлов, окружающий заданную область. На 4 этапе все тетраэдры, образованные с этими узлами, удаляются наряду с остальными тетраэдрами, оказавшимися "по ту сторону границы".

Этап 2. Восстановление "ребер" производится с помощью дополнительных узлов[4]. Заметим, что если в двумерном случае всегда возможно построить триангуляцию Делоне с ограничениями без использования дополнительных узлов, то в трехмерном случае это, как правило, невозможно.

Дополнительные узлы вставляются в точки пересечений "ребер" ограничений с гранями и ребрами тетраэдров. Заметим, что вариантов пересечения "ребра" с тетраэдром всего шесть (рис. 10). Соответственно, для каждого варианта используется свой шаблон разбиения тетраэдра. При этом встает вопрос согласования триангуляции на гранях соседних тетраэдров, поскольку некоторые случаи (рис. 10. в) допускают различные способы разбиения граней. Это проблема решается установкой следующих двух правил: 1) из всех вариантов всегда выбирается самое короткое ребро; 2) если ребра равны, проводится ребро от узла с самым меньшим глобальным номером (например).

Вспомним, что тетраэдр может пересекаться не одним "ребром", а сразу несколькими. Чтобы избежать ввода дополнительных шаблонов (поскольку, теоретически, "ребер", пересекающих тетраэдр, может быть неограниченно много), достаточно обрабатывать каждое "ребро" отдельно, по очереди. При обработке каждого "ребра" остальные, еще не обработанные, не учитываются, а после обработки "ребро" уже аппроксимировано цепочкой ребер триангуляции и естественным образом входит в сетку, поэтому указанная проблема исчезает.

Этап 3. На предыдущем этапе все "ребра" ограничений были аппроксимированы цепочками ребер сетки. Теперь нужно добиться того, чтобы все поверхности ограничений были представлены множеством смежных граней. Это также осуществляется вставкой дополнительных вершин - в точках пересечения поверхностей ограничения с ребрами сетки (см. рис. 9). Опять встает вопрос об однозначности разбиения граней, но теперь он несколько сложнее. В случае, если поверхность пересекает 3 ребра тетраэдра (рис. 9. а), то возможен такой вариант проведения ребер, при котором нижняя часть элемента - пятигранник (усеченный тетраэдр) - не разбивается на тетраэдры. Разрешить эту ситуацию можно с помощью дополнительного узла, вставляемого внутрь пятигранника. Тогда согласование ребер можно осуществлять по правилам, изложенным выше.

Этап 4. Удаление лишних тетраэдров, лежащих вне границы заданной области, не представляет какой-либо проблемы. Зато можно сказать, что после их удаления граница области будет полностью аппроксимирована гранями и ребрами построенной триангуляции. То же самое относится и к внутренним ребрам и поверхностям ограничений, если таковые были.

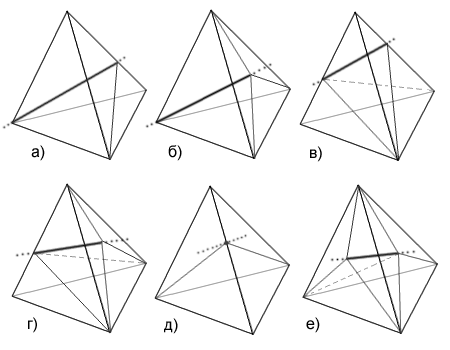
Рис. 10. Возможные варианты пересечения "ребра"ограничения с тетраэдром и соответствующие способы разбиения тетраэдра на части: а) вершина - ребро; б) вершина - грань; в) ребро - ребро; г) ребро - грань; д) ребро - вырожденный случай; е) грань - грань.

На рис. 11 представлен результат триангуляции с помощью описанного алгоритма области, являющей собой объединение икосаэдра и додекаэдра[5].

Рис. 11. Триангуляция области, представляющей собой объединение додекаэдра и икосаэдра (триангуляция Делоне с ограничениями)

Качество сеток, построенных данным методом, находится на среднем уровне (тетраэдры у границ могут иметь очень плохую форму), поэтому обычно дополнительно прибегают к одному из методов оптимизации.

В работах Б. Джо [23, 24] предложены другие варианты алгоритма, не использующие дополнительных точек и полностью основанные на локальных трансформациях, аналогичных "трейду".