Построение первичной сетки

Разработка и реализация алгоритмов

Трехмерной триангуляции

сложных пространственных областей:

Итерационные методы

 

Москва – 2006

Аннотация

Рассмотрены итерационные методы трехмерной дискретизации пространственных областей (построения тетраэдрических сеток): методы граничной коррекции, методы на основе критерия Делоне и методы исчерпывания. Приведены варианты алгоритмов для каждого из указанных методов. Обсуждены особенности построения сеток в сложных областях.

 

 

M.P. Galanin, I. A. Sheglov

Development And Implementation of Algorithms For Constrained Volume Triangulations: Iterative Algorithms

Abstract

Three main families of iterative algorithms for free and constrained simplicial volume triangulation are described: boundary correction (including "octree" algorithm), Delaunay-based methods and advancing front approach. For each method type an example algorithm is given.       

 

 

Содержание

1. Введение                                                                                                 3

2. Методы граничной коррекции                                                               4

2.1 Построение первичной сетки                                                      4

2.2 Коррекция первичной сетки                                                       6

3. Методы на основе критерия Делоне                                                  9

3.1 Построение триангуляции Делоне на заданном наборе точек     12

3.2. Триангуляция Делоне с ограничениями                             17

3.3 Особенности технической реализации алгоритмов на основе критерия Делоне                                                                      22

4. Методы исчерпывания                                                                     23

4.1 Пример алгоритма исчерпывания                                       26

Список литературы                                                                              30

  1. Введение

Среди двух классов методов триангуляции - прямых и итерационных - последние обладают достаточной универсальностью и поэтому, в отличие от прямых, могут быть использованы для триангуляции областей довольно произвольного вида. За эту универсальность приходится расплачиваться существенно большим потреблением ресурсов и более трудоемкой реализацией метода в конкретном алгоритме.

В настоящее время разработано большое количество программных пакетов на основе того или иного итерационного метода, реализующих построение сеток (частично или полностью) в автоматическом режиме. В основном эти пакеты коммерческие, что вполне оправдано с учетом затрачиваемых на их создание усилий, ведь трехмерное пространство имеет ряд неприятных особенностей, существенно затрудняющих жизнь разработчику [45].

Сетки, построенные итерационными методами, как правило, неструктурированы и неоднородны. Неструктурированность обусловлена тем, что топология сетки формируется в процессе построения, и поэтому естественно может варьироваться даже в пределах одной подобласти. По этой же причине однородность если и может возникнуть, то только случайно.

Поскольку перед построением сетки ничего нельзя сказать о ее будущей структуре, нельзя гарантировать и ее качества. Часто построенную сетку можно существенно улучшить с помощью одного из многочисленных методов оптимизации [16, 19, 34]. Этой возможностью обычно не пренебрегают, благо что время, затрачиваемое на оптимизацию, как правило, существенно меньше времени, затрачиваемого на построение.

Целью данной работы является рассмотрение и классификация существующих методов построения тетраэдрических сеток в трехмерных областях. Ввиду значительного объема информации ниже рассматриваются только так называемые "итерационные методы". Прямые методы описаны в [45].

Работа выполнена при частичной финансовой поддержке Российского фонда фундаментальных исследований (проект № 06-01-00421).

Методы граничной коррекции

В самом названии этой группы методов содержится их основная идея. "Наложив" на заданную область некоторую уже построенную сетку, можно отсечь от этой сетки все выходящие за пределы нужной области фрагменты, а затем скорректировать положение узлов, лежащих вблизи границы, так, чтобы они попали в "углы", на "ребра" и на "грани" области.

Таким образом, алгоритм разбивается на два различных этапа:
1) построение "первичной" сетки и 2) ее коррекцию. Поскольку эти этапы практически не связаны друг с другом, рассмотрим их отдельно.

Построение первичной сетки

Самый простой подход к решению этой задачи - это использование одного из методов на основе шаблонов. В этом случае в качестве области для построения первичной сетки выбирают одну из подходящих геометрических форм, для которых разработаны шаблоны (разумеется, эта область должна полностью включать в себя заданную). Как правило, в качестве такой "супер-области" используют параллелепипед, хотя в некоторых случаях (например, радиальной симметрии) удобнее использовать цилиндр.

Дискретизация на основе шаблонов подробно рассмотрена в работе [45], поэтому не будем более останавливаться на этом варианте; заметим лишь, что построенная при этом итоговая сетка получается близкой к равномерной, то есть линейные размеры ее элементов приблизительно равны. Это обусловлено тем, что при построении первичной сетки не используется никакой информации о геометрии заданной области.

Существует алгоритм, который позволяет учитывать эти особенности и таким образом строить своего рода адаптивные сетки (правда, адаптированные к геометрии, а не к конкретной задаче). Этот алгоритм был разработан группой Марка Шепарда (Mark Shephard) из университета Ренсселаера (США) в 80 годах ХХ столетия и получил название "octree" (его двумерный вариант называется "quadtree"). С тех пор было предложено несколько его разновидностей [30, 39, 40, 44]; рассмотрим одну из них.

Идея алгоритма заключается в следующем: исходная область помещается в кубическую сетку, элементы которой последовательно дробятся на более мелкие кубы до тех пор, пока размеры получаемых в итоге кубических ячеек не достигнут желаемой величины; при этом каждый куб дробится только в том случае, если его грани пересекаются границей области (либо внутри куба целиком оказывается особенности вроде отверстия или полости). Таким образом удается добиться "естественного" увеличения плотности узлов вблизи границ области и ее "особенных" участков. Чтобы избежать значительных перепадов размеров элементов, дополнительно вводят ограничение на степень "раздробленности" соседних элементов - она не должна отличаться более чем на единицу. Рис. 1 иллюстрирует идею метода для двумерного случая.

Рис. 1. Раздробление области на квадратные ячейки по алгоритму "quadtree"

 

Следующим этапом метода является построение треугольной (тетраэдрической) сетки на основе полученного разбиения на квадраты (кубы). Поскольку возможных вариантов размещения узлов на ребрах и гранях кубов/квадратов в такой сетке немного (для квадрата с учетом отражения и поворота - всего 6), для каждого варианта используется свой заранее заданный шаблон. На рис. 2 и рис. 3 показаны 2 набора таких шаблонов: "классический", предложенный Шепардом, и разработанный авторами вариант, основанный на вставке дополнительного узла, позволяющий получить сетки из подобных элементов (и лучшего качества).

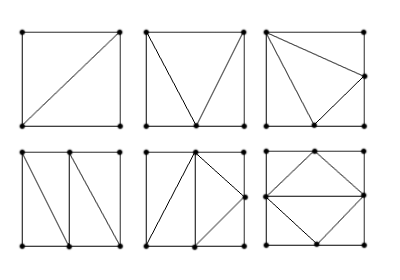
Рис. 2. "Классический" набор шаблонов для разбиения квадратов в методе "quadtree"

Рис. 3. Набор шаблонов с использованием дополнительного внутреннего узла, дающий лучшее качество сетки

 

На рис. 4 приведена сетка, получающаяся в результате применения указанных наборов шаблонов. Заметим, что описанный алгоритм без каких-либо особенностей переносится на случай 3 измерений, поэтому дополнительно рассматривать его нет смысла. Следует также обратить внимание, что полученная сетка не является структурированной, хотя в дальнейшем это не играет никакой роли (так как при граничной коррекции свойство структурированности в любом случае утрачивается).