Пример алгоритма исчерпывания

Рассмотрим алгоритм исчерпывания, разработанный вторым автором данной работы и предназначенный для построения равномерных сеток в произвольных областях.

Пусть необходимо построить сетку с желаемой средней длиной ребра, равной h (эту величину часто называют шагом триангуляции). В качестве исходных данных алгоритм требует два массива данных: массив, описывающий триангуляцию границы (фактически, начальный фронт; представляется в виде списка треугольников-граней) и массив вспомогательных точек F. Этот массив формируется так: заданная область помещается в супер-область (параллелепипед), которая равномерно заполняется вспомогательными точками F с шагом 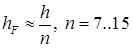 (то есть плотность их размещения должна быть на порядок больше плотности размещения узлов триангуляции.) Заметим, что, поскольку координаты этих узлов можно легко вычислять ( 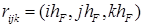), под этот массив не потребуется много памяти. Фактически, множество F будет описываться трехмерным массивом 1-битных булевых переменных (TRUE = точка существует, FALSE = точка удалена). Таким образом, хранение 8 миллионов элементов F потребует около мегабайта оперативной памяти. После формирования множества F из него удаляются все точки, лежащие вне заданной области. Оставшиеся точки будут представлять своего рода объемное растровое изображение заданной области. Именно с помощью множества F в этом алгоритме и решаются многие проблемы, указанные выше.

Поскольку алгоритм рассчитан на построение равномерных сеток, контрольная функция 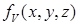 считается константой, равной  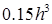(объем правильного тетраэдра с ребром h плюс допуск 25%).

Далее производятся следующие действия:

1. Формируется множество узлов G, состоящее из вершин фронта (т.е. изначально в него входят все существующие узлы сетки); для каждого узла G проводится оценка телесного угла. Эта оценка сводится к нахождению числа существующих (т.е., неудаленных) точек F, находящихся от данного узла на расстоянии не более чем 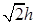 (что требует существенно меньших затрат ресурсов, чем прямое вычисление телесных углов).

2. Находится вершина 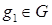 с наименьшим оценочным значением величины телесного угла и выбирается такая грань ( 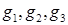) фронта, для которой сумма оценок величин телесных углов для 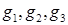минимальна.

3. Формируется множество 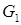 узлов G, находящихся от каждой из вершин выбранной грани на расстоянии не более  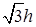(это множество может оказаться и пустым). Для каждого узла  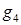из 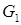 рассматривается тетраэдр ( 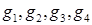), причем тетраэдр отбрасывается, если не выполняется хотя бы одно из следующих условий:

1) строго внутри этого тетраэдра нет ни одной удаленной точки F (существование таких точек на гранях допускается);

2) внутри этого тетраэдра нет других существующих узлов сетки, за исключением самих вершин этого тетраэдра;

3) тетраэдр не пересекается никаким существующим ребром сетки (считается, что тетраэдр пересекается ребром, не являющимся ребром этого тетраэдра, если у него с этим ребром есть хотя бы одна общая точка, не являющаяся вершиной этого тетраэдра.)[7];

4) объем тетраэдра не больше максимально допустимого ( ).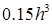

Из всех тетраэдров ( 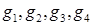) выбирается тетраэдр наилучшего качества [45] и производится переход к п. 5; если же тетраэдров, удовлетворяющих указанным условиям, не оказалось, то осуществляется переход к п. 4.

4. Находится такая точка 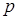 внутри еще неисчерпанной области, что:

1) тетраэдр ( 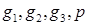) удовлетворяет всем условиям п. 3;

2) в шаре 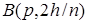 нет ни одной удаленной точки F (это предотвращает размещение узла p слишком близко от граней и вершин существующих тетраэдров).

Вариант алгоритма поиска узла p рассмотрен ниже.

5. Удаляются все вершины F, попавшие внутрь (и на границы) сформированного тетраэдра. Затем фронт обновляется по следующей схеме: рассматривается каждая грань сформированного тетраэдра и

1) если грань является гранью фронта, то она удаляется из фронта;

2) если грань НЕ является гранью фронта, она добавляется во фронт.

6. Если еще остались неудаленные точки F или (что эквивалентно) фронт не пуст (то есть область еще не исчерпана полностью), осуществляется переход к п. 1, иначе процесс окончен. 

Таким образом, массив F используется сразу для нескольких целей: для оценки величины телесного угла, для контроля правильности построения и для контроля размещения новых узлов. Также массив F удобно использовать для индикации процесса выполнения. Отношение числа удаленных во время работы алгоритма точек F к начальному числу существующих точек F фактически показывает, какая часть области уже исчерпана.

Вернемся к вопросу нахождения координат нового узла для построения тетраэдра (п. 4 описанного алгоритма). Пусть заданы три узла - .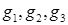

1. На первом шаге находятся 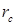 - центр масс треугольника (как среднее арифметическое координат его узлов) и единичная нормаль  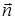к плоскости грани (через нормированное векторное произведение).

2. Далее определяется первое приближение для расстояния от 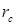 до искомой точки p (H), исходя из максимального объема тетраэдра: 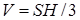. Заметим, что площадь грани S фактически найдена на предыдущем шаге (результат векторного произведения двух ребер равен удвоенной площади грани), а максимальный объем обусловлен значением контрольной функции.

3. Проверяется точка 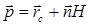. Если тетраэдр ( 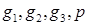) удовлетворяет всем требованиям, происходит переход к п. 6, иначе - к п. 4.

4. Проверяется точка 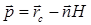. Если тетраэдр ( 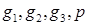) удовлетворяет всем требованиям, происходит переход к п. 6, иначе - к п. 5.

5. Полагают 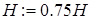 и переходят к п. 3.

6. Искомый узел найден.

Заметим, что в 99% случаев искомая точка находится на 1 или 2 итерации данного алгоритма.

В описанном выше алгоритме исчерпывания на каждом шаге из области изымается один тетраэдр. Сотрудник НАСА Ш. Пирзаде (Shahyar Pirzadeh) предложил другой вариант алгоритма, в котором за один раз из области изымается сразу целый слой тетраэдров (то есть на каждой итерации тетраэдры строятся сразу для всех граней текущего фронта) [32]. Вопреки ожиданию, этот вариант не позволяет сколько-нибудь существенно ускорить процесс построения (т.к. все новые тетраэдры все равно необходимо проверять на корректность), однако он избавляет от необходимости искать наиболее подходящую для построения тетраэдра грань. Это, однако, скорее минус, чем плюс, так как из-за этой особенности вариант Пирзаде менее надежен и может дать сбой на геометрически сложных областях. Вместе с тем на сравнительно простых областях он показывает неплохие результаты.

Сетки, построенные методами исчерпывания, как правило, обладают неплохим качеством, а последующая оптимизация положения узлов дает дополнительную прибавку к качеству. Подводя итог, заметим, что методы исчерпывания наиболее эффективны, если изначально задана триангуляция границы области. В этом и состоит их основное отличие от методов на основе критерия Делоне, для которых ситуация прямо обратная.

Список литературы

1. Шайдуров В.В. Многосеточные методы конечных элементов. - М., Наука, 1989. - 288с.

2. Скворцов А.В. Обзор алгоритмов построения триангуляции Делоне // Вычислительные методы и программирование, 2002, №3, c. 14-39.

3. Скворцов А.В. Алгоритмы построения триангуляции с ограничениями // Вычислительные методы и программирование, 2002, №3, c. 82-92.

4. I.Babushka, W.C. Rheinboldt. A-posteriori Error Estimates for Finite Element Method // Int. J. Numer. Meth. Eng.,Vol. 12, p.p. 1597-1615, 1978.  

5. T.J. Baker. Automatic Mesh Generation for Complex Three-Dimensional Regions Using a Constrained Delaunay Triangulation // Engineering With Computers, Springer-Verlag, № 5, p.p. 161-175, 1989.

6. M. Bern, D. Eppstein. Mesh Generation and Optimal Triangulation // Computing in Euclidean Geometry, World Scientific Publishing Co., p.p. 23-90, 1995.

7. D.K. Blandford, G. Blelloch, D. Cardoze, C. Kadow. Compact Representations of Simplicial Meshes In Two and Three Dimensions // Proceedings of 12th International Meshing Roundtable, Sandia National Laboratories, p.p.135-146, Sept. 2003.

8. H. Borouchaki, S.H. Lo. Fast Delaunay Triangulation In Three Dimensions // Computer Methods In Applied Mechanics And Engineering, Elsevier, Vol. 128, p.p. 153-167, 1995.

9. E.K. Buratynski. A Three-Dimensional Unstructured Mesh Generator for Arbitrary Internal Boundaries // Numerical Grid Generation in Computational Fluid Mechanics, Pineridge Press, p.p. 621-631, 1988.

10. P.R. Cavalcanti, U.T. Mello. Three-Dimensional Constrained Delaunay Triangulation: A Minimalist Approach // Proceedings of the 8th International Meshing Roundtable, p.p. 119-129, 1999.

11. Dey, K. Tamal, K. Sugihara, C.L. Bajaj. Delaunay Triangulations In Three Dimensions With Finite Precision Arithmetic // Computer Aided Geometric Design, North-Holland, № 9, p.p. 457-470, 1992.

12. H.N. Djidjev. Force-Directed Methods For Smoothing Unstructured Triangular And Tetrahedral Meshes // Proceedings of 9th International Meshing Roundtable, Sandia National Laboratories, p.p. 395-406, October 2000.

13. L. Durbeck. Evaporation: A Technique For Visualizing Mesh Quality // Proceedings of 8th International Meshing Roundtable, South Lake Tahoe, CA, U.S.A., p.p. 259-265, October 1999.

14. D.A. Field. Laplacian Smoothing And Delaunay Triangulations // Communications in Applied Numerical Methods, vol. 4, p.p. 709-712, 1988.

15. P.J. Frey, H. Borouchaki, P.-L. George. Delaunay Tetrahedralization Using an Advancing-Front Approach // Proceedings of 5th International Meshing Roundtable, Sandia National Laboratories, p.p. 31-46, October 1996. 

16. L.A. Freitag, C. Ollivier-Gooch. A Comparison of Tetrahedral Mesh Improvement Techniques // Proceedings of 5th International Meshing Roundtable, Sandia National Laboratories, p.p. 87-106, October 1996.

17. L.A. Freitag, C. Ollivier-Gooch. Tetrahedral Mesh Improvement Using Swapping and Smoothing // International Journal for Numerical Methods in Engineering, vol. 40, p.p. 3979-4002, 1995.

18. L.A. Freitag, C. Ollivier-Gooch. The Effect Of Mesh Quality On Solution Efficiency // Proceedings of 6th International Meshing Roundtable, Sandia National Laboratories, p.p.249, October 1997.

19. P.L. George. TET MESHING: Construction, Optimization and Adaptation // Proceedings of 8th International Meshing Roundtable, p.p.133-141, 1999.

20. N.A. Golias, T.D. Tsiboukis. An Approach to Refining Three-Dimensional Tetrahedral Meshes Based on Delaunay Transformations // International Journal for Numerical Methods in Engineering, John Wiley, № 37, p.p.793-812, 1994.

21. C. Hazlewood. Approximating Constrained Tetrahedralizations // Computer Aided Geometric Design, vol. 10, p.p. 67–87, 1993.

22. B. Joe. Delaunay Triangular Meshes in Convex polygons, SIAM J. Sci. Stat. Comput., Vol. 7, p.p. 514-539, 1986.

23. B. Joe. Construction Of Three-Dimensional Delaunay Triangulations Using Local Transformations // Computer Aided Geometric Design, Vol. 8, p.p. 123-142, 1991. 

24. B. Joe. Construction of Three-Dimensional Improved-Quality Triangulations Using Local Transformations // Siam J. Sci. Comput., vol. 16, p.p. 1292-1307, 1995.

25. R.W. Lewis, Yao Zheng, D.T. Gethin. Three-Dimensional Unstructured Mesh Generation: Part 3. Volume Meshes // Computer Methods In Applied Mechanics And Engineering, Elsevier, Vol 134, p.p.285-310, 1996.

26. A.Liu, B. Joe. On The Shape Of Tetrahedra From Bisection // Mathematics of Computation, vol. 63, №207, 141–154, 1994.

27. S.H. Lo. Volume Discretization into Tetrahedra-I. Verification and Orientation of Boundary Surfaces // Computers and Structures, Pergamon Press, Vol. 39, № 5, p.p. 493-500, 1991.

28. S.H. Lo. Volume Discretization into Tetrahedra - II. 3D Triangulation by Advancing Front Approach // Computers and Structures, Pergamon, Vol. 39, № 5, p.p. 501-511, 1991.

29. R. Lohner. Generation Of Three-Dimensional Unstructured Grids By The Advancing Front Method //Proceedings of the 26th AIAA Aerospace Sciences Meeting, Reno, Nevada, 1988.

30. S.J. Owen. A Survey of Unstructured Mesh Generation Technology // Proceedings of 7th International Meshing Roundtable, p.p. 239-269, Dearborn, MI, 1998.

31. V.N. Parthasarathy, C.M. Graichen, A.F. Hathaway. A Comparison of Tetrahedron Quality Measures // Finite Elements in Analysis and Design, Elsevier, №. 15, p.p. 255-261, 1993.

32. S. Pirzadeh. Unstructured Viscous Grid Generation by Advancing-Layers Method // AIAA-93-3453-CP, AIAA, p.p. 420-434, 1993.

33. V.T. Rajan. Optimality of Delaunay Triangulation in 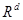// Proc. 7th ACM Symp. Comp. Geometry, p.p. 357-363, 1991.

34. A.Rassineux. Generation and Optimization of Tetrahedral Meshes by Advancing Front Technique // International Journal for Numerical Methods in Engineering, Wiley, Vol. 41, p.p. 651-674, 1998.

35. S. Rebay. Efficient Unstructured Mesh Generation by Means of Delaunay Triangulation and Bowyer-Watson Algorithm // Journal Of Computational Physics, vol. 106, p.p. 125-138, 1993.

36. M.-C. Rivara. Selective Refinement/Derefinement Algorithms For Sequences Of Nested Triangulations // International Journal for Numerical Methods in Engineering, №28, p.p. 2889-2906, 1998.

37. M.-C. Rivara, C. Levin. A 3D Refinement Algorithm Suitable For Adaptive And Multigrid Techniques // Communications in Applied Numerical Methods, № 8, p.p. 281-290, 1998.

38. J. Ruppert. A Delaunay refinement algorithm for quality 2-dimensional mesh generation // Journal of Algorithms, №18, p.p. 548-585, 1995.

39. M.S. Shephard, M.K. Georges. Three-Dimensional Mesh Generation by Finite Octree Technique // International Journal for Numerical Methods in Engineering, vol. 32, p.p. 709-749, 1991.

40. M.S. Shephard, F. Guerinoni, J.E. Flaherty, R.A. Ludwig, P.L. Baehmann. Finite octree mesh generation for automated adaptive 3D Flow Analysis // Numerical grid generation in computational Fluid mechanics, Miami, 1988

41. K. Shimada, D.C. Gossard. Bubble Mesh: Automated Triangular Meshing of Non-manifold Geometry by Sphere Packing // Proceedings of 3rd Symposium on Solid Modeling and Applications, p.p. 409-419, 1995.

42. K. Shimada, A. Yamada, T. Itoh. Anisotropic Triangular Meshing of Parametric Surfaces via Close Packing of Ellipsoidal Bubbles // Proceedings of 6th International Meshing Roundtable, p.p. 375-390, 1997.

43. D.F. Watson. Computing the Delaunay Tessellation with Application to Voronoi Polytopes // The Computer Journal, Vol. 24(2), p.p. 167-172, 1981.

44. M.A. Yerry, M.S. Shephard. Three-Dimensional Mesh Generation by Modified Octree Technique // International Journal for Numerical Methods in Engineering, Vol. 20, p.p. 1965-1990, 1984.

45. Галанин М.П., Щеглов И.А. Разработка и реализация алгоритмов трехмерной триангуляции сложных пространственных областей: прямые методы. Препринт ИПМ им. М.В. Келдыша РАН, 2006, в печати.

[1] "Сплайнами" в данном случае называются фрагменты поверхностей

[2] Следует отметить, что свойство минимизации радиусов описанных сфер сохраняется; более того, как показывает работа сотрудника исследовательского центра IBM В.Т. Раджана (V.T. Rajan), это справедливо и для n-мерного случая [33]

[3] В англоязычной литературе также часто называется "2-to-3 flip"

[4] Это т.н. Steiner points, т.е. узлы Штейнера - дополнительные узлы, не входившие в изначальный набор

[5] П. Кавальканти, У. Мелло [10]

[6] из архива Dassault-Aviation

[7] Может показаться, что из условия 3 следует условие 2, но на самом деле это не так. Например, существующий тетраэдр может целиком оказаться внутри проверяемого тетраэдра.