 |
Главная |
Простейшие тригонометрические уравнения
|
из
5.00
|
Уравнением называется равенство, содержащее переменную. А уравнения, в которых неизвестные содержатся под знаком тригонометрических функций, называются тригонометрическими уравнениями.
Решением уравнения с неизвестным х называют число хо, при подстановке которого в уравнение вместо х получается верное числовое равенство. Отличительная особенность тригонометрических уравнений – бесконечное множество корней. Эта особенность связана с характерным свойством тригонометрических функций – периодичностью. Решить уравнение – это значит найти все его решения или показать, что их нет.
Решение любого уравнения: сводится к стандартному виду. Путем преобразований линейные уравнения сводят к виду ах = в, квадратные – к виду ax2 + вx + c =0.
Необходимость классификации уравнений вызывается невозможностью найти общий метод их решения. Известно, что целые алгебраические уравнения со времен Декарта (1596-1650) классифицируются по степени уравнения. Чем выше степень таких уравнений, тем сложнее взаимная связь неизвестного с коэффициентами уравнения и тем труднее выразить это неизвестное через коэффициенты.
В тригонометрии предпринимались попытки создавать свою специфическую классификацию. Пример такой классификации, содержащей восемь типов тригонометрических уравнений, приводится в пособии И.К. Андронова, А.К. Окунева «Курс тригонометрии». Классифицировать тригонометрические уравнения по степени не имеет большого смысла, так как тригонометрические уравнения допускают повышение и понижение степени за счет использования формул половинного и двойного аргумента. Очевидно, что классифицировать тригонометрические уравнения имеет смысл с опорой на методы их решения. Здесь я попытаюсь показать, с какими методами решения тригонометрических уравнений мы сталкиваемся в учебнике для 10-11 классов общеобразовательных учреждений «Алгебра и начала анализа» под редакцией А. Н. Колмогорова (2001 г.).
Решение тригонометрических уравнений выполняется в большинстве случаев (с помощью различных преобразований) путём сведения их к простейшим тригонометрическим уравнениям. Поэтому и работу с тригонометрическими уравнениями естественно начинать с простейших тригонометрических уравнений.
Уравнение f ( x ) = а, где а – данное число, а f ( x ) – одна из основных тригонометрических функций, называют простейшим тригонометрическим уравнением. В школьном курсе рассматриваются следующие простейшие тригонометрические уравнения: sin t = a , cos t = a , tg t = a , ctg t = a .
Рассмотрим, при каких значениях а простейшие тригонометрические уравнения разрешимы (имеют решения) и как правильно находить все решения таких уравнений.
А) Уравнение sin t = a .
Так как множество значений функции у = sinx – отрезок [– 1; 1], то уравнение sin t = a разрешимо только в том случае, когда |а| ≤ 1. И тогда решение данного уравнения находится по формуле: t = (– 1) n arcsin a + π n , где n Î Z. Соответственно, если |а| > 1, то уравнение не имеет действительных корней. Это обстоятельство следует хорошо помнить, т. к. забывая об этом, часто допускают ошибки. Например, при решении уравнения sin t =  часто, не обращая внимания на то, что
часто, не обращая внимания на то, что  > 1, пишут ответ: t = (– 1) n arcsin
> 1, пишут ответ: t = (– 1) n arcsin  + π n , где n Î Z , который не имеет никакого смысла, т. к. функция arcsin a не определена в точке а =
+ π n , где n Î Z , который не имеет никакого смысла, т. к. функция arcsin a не определена в точке а =  (эта точка не принадлежит области определения функции arcsin a).
(эта точка не принадлежит области определения функции arcsin a).
Если а = – 1; 0; 1, то рассматривают частные случаи решения данного уравнения.
При а = – 1 х = 
а = 0 х = π n , где n Î Z ;
а = 1 х = 
Б) Уравнение cos t = a .
Это уравнение имеет решения тогда и только тогда, когда |а| ≤ 1. Если это условие выполнено, то все решения уравнения cos t = a записываются в виде: t = ± arccos а + 2π n , где n Î Z . Соответственно, если |а| > 1, то уравнение не имеет действительных корней.
Если а = – 1; 0; 1, то также рассматривают частные случаи решения данного уравнения.
При а = – 1 х = 
а = 0 х = 
а = 1 х = 
В) Уравнение tg t = a .
Данное уравнение имеет решения при любом значении а Î (– µ ; µ ). Все решения уравнения задаются формулой t = arctg а + π n , где n Î Z . Частные случаи здесь не рассматривают.
Г) Уравнение с tg t = a .
Данное уравнение имеет решения при любом значении а Î (– µ ; µ ). Все решения уравнения задаются формулой t = ar с ctg а + π n , где n Î Z . Частные случаи здесь также не рассматривают.
Ряд уравнений путём элементарных преобразований: перенос слагаемых из одной части уравнения в другую, деление обеих частей уравнения на одно и тоже число, отличное от нуля, также очень легко сводятся к простейшим.
При решении простейших тригонометрических уравнений вида А sin (вх + с) = d , А cos (вх + с) = d , А tg (вх + с) = d , А ctg (вх + с) = d следует обратить внимание на то, что они приводятся к виду sin (вх + с) = а, cos (вх + с) = а, tg (вх + с) = а, ctg (вх + с) = а.
Сведение тригонометрических уравнений к простейшим тригонометрическим уравнениям выполняется различными способами. Первоначально надо рассмотреть тригонометрические уравнения, в которых под знаком тригонометрических функций стоит более сложное выражение, зависящее от х. для решения таких уравнений можно обозначить выражение, стоящее под знаком тригонометрической функции, одной буквой; решить простейшее тригонометрическое уравнение, а потом найти х, решая алгебраическое уравнение.
К таким уравнениям относятся уравнения:
| sin t = a | № 138, 139, 142(а, в), 143(а), 144(а), 145(б, г), 146(б), 173(в) |
| cos t = a | № 136, 137, 142(б, г), 143(б), 144(в), 145(а), 146(г), 172(б) |
| tg t = a | № 140(а, в, г), 141(а, в), 143(г), 144(б), 145(в), 146(в), 173(б) |
| ctg t = a | № 140(б), 141(б, г), 143(б), 144(г) |
Покажу на примерах, как решаются такие уравнения с применением выше указанных формул.
№ 136(б).
с os x = – ,
х = ± arccos (– ) + 2π n , n Î Z ,
х = ± 
Ответ: х = ± 
№ 139(б).
2 sin x +  = 0,
= 0,
2 sin x = –  ,
,
sin x = –  ,
,
х = (– 1)narcsin (–  ) + π n, n Î Z,
) + π n, n Î Z,
х = (– 1) n + 1  + π n , n Î Z .
+ π n , n Î Z .
Ответ: х = (– 1) n + 1  + π n , n Î Z .
+ π n , n Î Z .
№ 144(г).
ctg (– ) = 1,
– ctg = 1,
ctg = – 1,
= ar с ctg (– 1) + π n , n Î Z ,
=  + π n , n Î Z ,
+ π n , n Î Z ,
х = 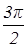 + 2π n , n Î Z .
+ 2π n , n Î Z .
Ответ: х = 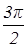 + 2π n , n Î Z .
+ 2π n , n Î Z .
№ 145(в).
 tg (
tg (  ) = 3,
) = 3,
tg (  ) =
) =  ,
,
 = arctg
= arctg  + π n, n Î Z,
+ π n, n Î Z,
 =
=  + π n , n Î Z ,
+ π n , n Î Z ,
 = π n , n Î Z ,
= π n , n Î Z ,
х = 3π n , n Î Z .
Ответ: х = 3π n , n Î Z .
Проблема решения тригонометрических уравнений состоит не в большом количестве разнообразных формул, а в выборе направления, по которому необходимо двигаться для решения уравнения. Первый шаг на пути решения тригонометрического уравнения – это попытка отнести его к какому-либо типу, и если это удаётся, то применить характерный для данного типа уравнения приём. Рассмотрим основные типы уравнений, предлагаемых в школьном учебнике под редакцией А. Н. Колмогорова. В учебном пособии приёмы решения тригонометрических уравнений не конкретизируются, а рассматриваются на нескольких конкретных примерах.
Для решения тригонометрических уравнений чаще всего используется два метода: введения новой переменной и разложения на множители.
Одним из самых общих методов решения тригонометрических уравнений является сведение тригонометрического уравнения к алгебраическому относительно одной тригонометрической функции с использованием тригонометрических формул: cos 2 х = 1 – sin 2 х, sin 2 х = 1 – cos 2 х, 

Уравнения вида sin ах ± sin вх = 0, cos ах ± cos вх = 0 решаются заменой суммы (разности) синусов и косинусов произведением.
Часто, особенно при решении квадратного уравнения относительно одной из тригонометрических функций, используется метод введения новой переменной.
Интерес вызывают и уравнения, сводимые к однородным: а × sin х + в × с os x = 0, а × sin 2 х + в × sin х × с os x + с × с os 2 x = 0
|
из
5.00
|
Обсуждение в статье: Простейшие тригонометрические уравнения |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

