Тригонометрические уравнения, сводящиеся к квадратным

 

Сведение тригонометрического уравнения к алгебраическому относительно одной тригонометрической функции – один из самых общих методов решения тригонометрических уравнений. В этом разделе рассмотрим уравнения, которые после введения нового неизвестного t = f ( x ), где f ( x ) – одна из основных тригонометрических функций, превращаются в квадратные. К таким уравнениям можно отнести уравнения вида:                             asin ² x + в sin x + c = 0,  а cos ² x + в sin x + c = 0 и т. д. Но в большинстве случаев приходится исходное уравнение преобразовать так, чтобы оно приобрело нужный вид. Для этого чаще всего используется основное тригонометрическое тождество                                     sin ² х + cos ² х = 1.

В учебнике это: № 164, 165, 166, 167, 168(б, г), 171(б, г).

Покажу на примерах, как решаются такие уравнения.

№164( а ).

2 sin ² x + sin х – 1 = 0.

Введём новую переменную: t = sin х. Тогда данное уравнение можно записать в виде: 2 t ² + t – 1 = 0. это квадратное уравнение. Его корни: t ₁ = – 1; t ₂ = . Тогда sin х = –1 и           sin х = – . Решим каждое из получившихся простейших уравнений.

1)  sin х = –1 (это частный случай),

х =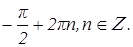

2) sin х = – ,

х = (– 1)ⁿarcsin (– ) + π k, k Î Z,

х = (– 1)^{k + 1}  + π k, k Î Z.

Ответ: х _n = х _k = (– 1)^{k + 1}  + π k, k Î Z.

№ 166( в ).

4 с os x = 4 – sin²x,

4 с os x = 4 – (1 – cos²x),

4 с os x = 4 – 1 + cos²x,

cos ² x – 4с os x + 3 = 0.

Пусть cos x = t, тогда t² – 4 t + 3 = 0.

Так как а + в + с = 0, то t ₁ = 1, t ₂ = 3.

Если t = 1, то cos x = 1,

                   х = 2π n , n Î Z .

Если t = 3, то cos x = 3,

                  корней нет, т.к. 3 Ï [– 1; 1].

Ответ: х = 2π n , n Î Z . 

 

№ 16 7 ( б ).

tg x – 2 ctg x + 1 = 0.

Применим формулу: .

Получим: tg x – 2 × 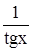 + 1 = 0.

Пусть tg x = t, тогда t –  + 1 = 0,

t ² + t – 2 = 0 (при условии t ≠ 0),

 

Так как а + в + с = 0, то t ₁ = 1, t ₂ = – 2.

Если t = 1, то tg x = 1,

                  х = arctg 1 + π n , n Î Z ,

                  х _n =  + π n , n Î Z .

Если t = – 2, то tg x = – 2,

                     х = arctg (– 2) + π k , k Î Z ,

                  x_k = – arctg 2 + π k , k Î Z .

Ответ: х _n =  + π n, n Î Z, x_k = – arctg 2 + π k, k Î Z.

 

Однородные уравнения

 

Здесь я рассмотрю довольно часто встречающиеся на практике тригонометрические уравнения специального вида.

Рассмотрим уравнения вида а_о × sinⁿ х + a ₁ × sin^{n – 1} х × с os x + a ₂ × sin^{n – 2} х × с os ² x + … + a _n × с os ⁿ x = 0, где а_о, a ₁ , a ₂ , …, a _n – действительные числа. Здесь в каждом слагаемом сумма показателей степеней синуса и косинуса левой части уравнения одна и та же и равна n.

Такое уравнение называется однородным относительно sin х и с os x , а число n называют показателем однородности.

Рассмотрим более подробно однородные уравнения с показателями однородности 1 и 2, т.к. в школьном курсе алгебры рассматриваются только такие однородные уравнения.

I ) Сначала скажу о решении однородных тригонометрических уравнений первой степени, причём рассмотрю только самый общий случай, когда оба коэффициента а и в отличны от нуля, т. к., если а = 0, то уравнение принимает вид в × с os x = 0, т. е. с os x = 0 – такое уравнение отдельного обсуждения не заслуживает; аналогично при в = 0 получаем sin х = 0, что тоже не требует отдельного обсуждения. Итак, при n = 1 имеем уравнение     а × sin х + в × с os x = 0 – это однородное уравнение первой степени, где а ≠ 0, в ≠ 0. 

Разделив обе части уравнения почленно на с os x , получим уравнение равносильное данному: а × tg x + в = 0 или tg x = – , откуда х = – arctg  + π n , n Î Z .

Необходимо помнить, что делить обе части уравнения на одно и то же выражение можно только в том случае, когда мы уверены, что это выражение нигде не обращается в нуль (на 0 делить нельзя!). Мы должны быть уверены в том, что с os x отличен от нуля. Предположим, что с os x = 0. Тогда однородное уравнение а × sin х + в × с os x = 0 примет вид а × sin х = 0, т. е. sin х = 0 (ведь у нас коэффициент а отличен от нуля). Получается, что и с os x = 0, и sin х = 0, а это невозможно, т. к. sin х и с os x обращаются в нуль в различных точках. Итак, в однородном тригонометрическом уравнении первой степени деление обеих частей уравнения на с os x – вполне благополучная операция.

Уравнения вида а × sin m х + в × с os mx = 0 тоже называют однородными тригонометрическими уравнениями первой степени. Для их решения обе части уравнения делят на с os mx .

II ) Рассмотрим теперь однородное тригонометрическое уравнение второй степени. При n = 2 имеем однородное уравнение вида а × sin ² х + в × sin х × с os x + с × с os ² x = 0.

Если коэффициент а отличен от нуля, т. е. в уравнении содержится член sin ² х с каким-то коэффициентом, рассуждая как и выше, нетрудно убедиться в том, что при интересующих нас значениях переменной с os x не обращается в нуль, а потому можно обе части уравнения разделить почленно на с os ² x . Что это даст?  

Мы получим уравнение равносильное данному уравнению: а × tg ² x + в × tg x + с = 0. Далее решение уравнения сводится к решению квадратного уравнения относительно tg x .

Таким методом решаются следующие номера из учебника: № 169, 170(а,г),    

III ) Пусть теперь в однородном тригонометрическом уравнении а × sin ² х + в × sin х × с os x + с × с os ² x = 0 коэффициент а равен 0, т. е. отсутствует член sin ² х. Тогда уравнение принимает вид: в × sin х × с os x + с × с os ² x = 0.

Это уравнение можно решить разложением на множители:

с os x (в × sin х + с × с os x ) = 0,

с os x = 0 или в × sin х + с × с os x = 0.

Получилось два уравнения, о решении которых говорилось выше.

Аналогично обстоит дело и в случае, когда с = 0, т. е. когда однородное уравнение имеет вид а × sin ² х + в × sin х × с os x = 0 (здесь можно вынести за скобки sin х).

Фактически получился алгоритм решения уравнения

а × sin ² х + в × sin х × с os x + с × с os ² x = 0:

1) Посмотреть есть ли в уравнении член а sin ² х.

2) Если член а sin ² х в уравнении содержится (т. е. а ≠ 0), то уравнение решается делением обеих его частей на с os ² x и последующим введение новой переменной t = tg x .

3) Если член а sin ² х в уравнении не содержится (т. е. а = 0), то уравнение решается методом разложения на множители: за скобки выносят с os x .

Также дело обстоит и в однородных уравнениях вида:

а × sin ² m х + в × sin m х × с os mx + с × с os ² mx = 0.

В учебнике для 10-11 классов к этому типу уравнений относится немного уравнений: №169, №170(а, г), №171(в), №172(а, в).

Хочется отметить, что некоторые уравнения, не являющиеся однородными, могут быть сведены к однородным после соответствующих преобразований.

№170(а).

4 sin ² х – sin 2 x = 3.

Применим формулы: sin 2 x = 2 sin x cos x , sin ² х + с os ² x = 1. Получим:

4sin² х – 2sin x cos x = 3(sin² х + с os² x),

4 sin ² х – 2 sin x cos x – 3 sin ² х – 3с os ² x = 0,

sin² х – 2sin x cos x – 3 с os² x = 0. Это однородное уравнение 2-ой степени. Разделим его на с os ² x

tg ² х – 2 tg х – 3 = 0.

Пусть tg х = t , тогда: t ² – 2 t – 3 = 0.

Так как а + с = в, то t ₁ = – 1, t ₂ = 3.

Если t = – 1, то tg х = – 1,

                      х = arctg (– 1) + π n , n Î Z ,

                      х _n = –  + π n , n Î Z .

Если t = 3, то tg х = 3,

                  x_k = arctg 3 + π k, k Î Z.

Ответ: х _n = –  + π n, n Î Z, x_k = arctg 3 + π k, k Î Z.

№171(а).

2 sin ² х = sin 2 x .

Применим формулу sin 2 x = 2 sin x cos x .

2sin² х – sin x cos x = 0,

2sin x(sin x – cos x) = 0,

2sin x = 0          или             sin x – cos x = 0,

sin x = 0                                    tg х = ,

х _n = πn, n Î Z                           x_k = arctg  + π k, k Î Z,

                                                  x_k =  + π k, k Î Z.

Ответ: х _n = πn, n Î Z, x_k =  + π k, k Î Z.