На тему: «Исследование элементарных функций».

                                    Выполнила: Квашенко Д.В.

                                         Проверил: Адольф В.А.

                        г. Красноярск

                                2005г.

                    Содержание:

 

 

· Определение элементарных функций…………….3

· Функция и её свойства ……………………………………..3

· Способы задания функции……………………………….4

· Определение функции……………………………………..4

· Исследование элементарных функций………....6

а) Линейная функция…………………………….......7

б) Степенная функция…………………………………..8

в) Показательная функция……………………………9

г) Логарифмическая функция……………………..10

д) Тригонометрическая функция………………..11

o Y = sin x ……………………………….…11

o Y = cos x …………………………………13

o Y = tg x …………………………………..14

o Y = ctg x …………………………………15

е ) Обратно тригонометрическая функция..16

o Y = arcsin x …………………………….16

o Y = arccos x ……………………………17

o Y = arctg x ……………………………..18

o Y = arcctg x …………………………….19

· Список литературы………………………………………..20

 

    Определение элементарных функций.

 

Функции С (постоянная), xⁿ, а^х, 1оg_а х, sin х, соs х, tg х, ctg x, аrcsin х, аrccos х, аrctg х называются простейшими элементарными функциями.

Применяя к этим функциям арифметические действия или операции функции от функции, мы будем получать новые более сложные фун­кции, которые называются элементарными функциями.

Например, у = sin (xⁿ) — элементарная функ­ция.

Элементарные функции нам известны из школьной математики.

 

 

Функция, и её свойства:

Функция - зависимость переменной у от переменной x , если каждому значению х соответствует единственное значение у.   

● Переменная х - независимая переменная или аргумент.

● Переменная у - зависимая переменная.

● Значение функции - значение у, соответствующее заданному

значению х.

● Область определения функции - все значения, которые принимает независимая переменная.

● Область значений функции (множество значений)- все значения, которые принимает функция.

● Функция является четной - если для любого х из области определения функции выполняется равенство f ( x )= f (- x ).

● Функция является нечетной - если для любого х из области определения функции выполняется равенство f (- x )=- f ( x ).

● Возрастающая функция - если для любых х₁ и х₂, таких, что х₁< х₂, выполняется неравенство f (х₁)< f (х₂).

● Убывающая функция - если для любых х₁ и х₂, таких, что х₁< х₂, выполняется неравенство f (х₁)> f (х₂) .

 

 

Способы задания функции:

●Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у= f ( x ), где f ( x ) - заданная функция с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически.

●На практике часто используется табличный способ задания функции. При этом способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента.

 

Определение функции.

 

    Функция, прежде всего, – это одно из основных понятий математического анализа, и чтобы далее рассматривать различные функции, следует дать определение функции.

    Пусть даны две переменные x и y с областями изменения X и Y. Предположим, что переменной x может быть приписано произвольное значение из области X без каких-либо ограничений. Тогда переменная y называется функцией от переменной x в области её изменения X, если по некоторому правилу или закону каждому значению x из X ставится в соответствие одно определенное значение y из Y.

     Независимая переменная x называется также аргументом функции.

     В этом определении существенны два момента: во-первых, указание области X изменения аргумента x (её называют также областью определения функции) и, во-вторых, установление правила или закона соответствия между значениями x и y (Область Y изменения функции обычно не указывается, поскольку самый закон соответствия уже определяет множество принимаемых функцией значений).

       Можно в определении понятия функции стать на более общую точку зрения, допуская, чтобы каждому значению x из X отвечало не одно, а несколько значений y (и даже бесконечное множество их). В подобных случаях функцию называют многозначной, в отличие от однозначной функции, определенной выше.

     Для указания того факта, что y есть функция от x, пишут:

y=f (x), y=g (x), y=F (x) и т.п.

     Буквы f, g, F, … характеризуют именно то правило, по которому получается значение x, отвечающее заданному y. Поэтому, если одновременно рассматриваются различные функции от одного и того же аргумента x, связанные с различными законами соответствия, их не следует обозначать одной и той же буквой.

    Хотя именно буква f связана со словом “функция”, но для обозначения функциональной зависимости может применяться и любая другая буква; иногда даже повторяют одну и ту же букву y: y=y(x). В некоторых случаях пишут аргумент и в виде значка при функции, например, .

  Если, рассматривая функцию y=f(x), мы хотим отметить её частное значение, которое отвечает выбранному частному значению x, равному , то для обозначения его употребляют символ f( ). Например, если

F (x)= , g (t)= 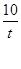, то f(1) означает численное значение функции f(x) при x=1, т.е. попросту число , аналогично, g(5) означает число 2, и т. д.

    Теперь обратимся к самому правилу, или закону соответствия между значениями переменных, которое составляет сущность понятия функциональной зависимости.

     Наиболее просто осуществление этого правила с помощью формулы, которая представляет функцию в виде аналитического выражения, указывающего те аналитические операции или действия над постоянными числами и над значением x, которые надо произвести, чтобы получить соответствующее значение y. Этот аналитический способ задания функции является наиболее важным для математического анализа.

      Однако будет ошибочным думать, что это – единственный способ, которым может быть задана функция. В самой математике нередки случаи, когда функция определяется без помощи формулы. Такова, например, функция E(x) – “целая часть числа x”. Например,

E (1)=1, E (2,5)=2, E ( )=3, E (- )=-4 и. т.,

хотя никакой формулы, выражающей E(x), у нас нет.

     Функция, все значения которой равны между собой, называется постоянной. Постоянную функцию обозначают C (f (x) = C).

     Функция f (x) называется возрастающей (убывающей) на множестве X, если для любой пары чисел и этого множества из неравенства 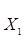 <  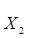следует, что f ( ) < f ( ) (f (  ) > f (  )).

     Функция f(x) называется четной, если область её определения X есть множество, симметричное относительно начала координат, и при любом x из X имеет место равенство f(-x)=f(x).

График четной функции симметричен относительно оси Oy.

      Функция f(x) называется нечетной, если область её определения X есть множество, симметричное относительно начала координат, и если при любом x из X имеет место равенство  f(-x)=-f(x).

График нечетной функции симметричен относительно начала координат.

       Сумма и разность двух четных (нечетных) функций есть функция четная (нечетная).

   Действительно, пусть y(x)=f(x) + g(x). Тогда, если f(x) и g(x) – четные, то y (-x) = f(-x) + g(-x) = f (x) + g (x) = y (x). Если же f (x) и g (x) – нечетные функции, то функция y (x) также будет нечетной, y (-x) = f (-x) + g (-x) = -f (x) – g (x) = -[f (x) + g (x)] = -y (x). (Для разности доказательство аналогичное).

       Произведение двух четных или двух нечетных функций есть функция четная, а произведение четной функции на нечетную – нечетная функция.

        В самом деле, пусть y (x) = f (x)*g (x) и f (x) и g (x) – четные функции, тогда y (-x) = f (-x)*g (-x) = f (x)*g (x) = y (x); если f (x) и g (x) – нечетные функции, то y (-x) = f (-x)*g(-x) = [-f (x)]*[-g(x)] = y (x); если же f (x) – четная, а g (x) – нечетная функции, то y (x) = f (x)*g (-x) = f (x)*[-g (x)] = -y (x).

  Функция f (x) называется периодической, если существует число Т 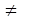0 такое, что для любого значения x из области определения функции выполняется равенство f (x - T) = f (x) = f (x + T). Число T называется периодом функции. Если T – период функции, то её периодом является также число – T, так как f (x-T) = f [(x - T) +T] = f (x).

    Если T – период функции, то её периодом будет также и число kT, где k – любое целое число (k= 1, 2, 3; …). Действительно, f (x 2T) = f [(x T) T] = f (x T) = f (x), f (x  3T) = f [(x  2T) T] = f (x  2T) = f (x  2T) = f (x);обычно под периодом функции понимают наименьший из положительных периодов, если такой период существует.