Исследование аппроксимации и сходимости

2.1. Аппроксимация дифференциального уравнения. Ранее рассматривалась краевая задача

 (k(x) u’(x))’ – q(x) u(x) + f(x) = 0, 0 < x < l,                                    (1)

– k(0) u’(0) + b u(0) = m ₁ , u(l) = m ₂ ,                                                  (2)

k(x) ³ c₁ > 0, b ³ 0,

для которой интегро-интерполяционным методом была построена разностная схема

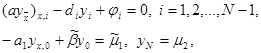(3)

(4)

 

где

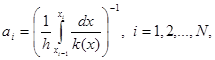(5)

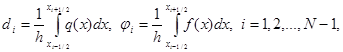(6)

 

 

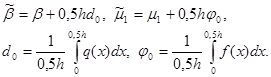Обозначим через Lu(x) левую часть уравнения (1) и через L_hy_i – левую часть уравнения (3), т.е.

 

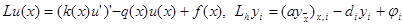Пусть u (x) – достаточно гладкая функция и u (x_i) – ее значение в точке x_i сетки

w _h = {x_i = ih, i = 0, 1, …,N, hN = l}                                                   (7)

 

Говорят, что разностный оператор L_h аппроксимирует дифференциальный оператор L в точке x=x_i, если разность L_h u _i – L_h u (x_i) стремится к нулю при h®0. В этом случае говорят также, что разностное уравнение (3) аппроксимирует дифференциальное уравнение (1).

Чтобы установить наличие аппроксимации, достаточно разложить по формуле Тейлора в точке x=x_i значения u _{i ± 1} = u (x_i ± h), входящие в разностное выражение L_h u _i. Большая часть этой работы проделана в предыдущей главе, где показано, что при условиях

 

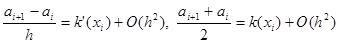(8)

 

выполняется соотношение

 

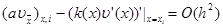Если кроме того, докажем, что

 

d_i = q(x_i) + O(h²), j _i = f(x_i) + O(h²)                                                 (9)

 

то тем самым будет установлено, что оператор L_h аппроксимирует L со вторым порядком по h, т.е.

 

L_h u _i – L u (x_i) = O(h²), i = 1, 2,…, N–1                                              (10)

 

Итак, доказательство второго порядка аппроксимации сводится к проверке сводится к проверке условий (8), (9) для коэффициентов (5), (6). Проверим сначала выполнение условий (8). Обозначая p(x) = k^-1(x), получим

 

 

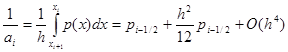следовательно,

 

 

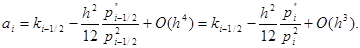Аналогично

 

 

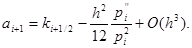Отсюда получим

 

 

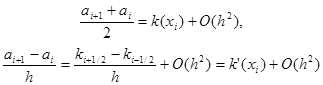т.е. условия (8) выполнены. Условия (9) выполнены в силу того, что замена интегралов (6) значениями q_i, f_i соответствует приближенному вычислению этих интегралов по формуле прямоугольников с узлом в середине отрезка интегрирования.

2.2. Аппроксимация граничного условия. Исследуем погрешность аппроксимации разностного граничного условия (4). Обозначим l_h u (0) = –a₁ u _{x, 0} + b u ₀. Если u (x) – произвольная достаточно гладкая функция, то очевидно

l_h u (0) = –k(0) u ’(0) + b u (0) + O(h),

 

т.е. имеет место аппроксимация первого порядка по h. Однако если u =u(x) – решение задачи (1), (2), то разностное граничное условие (4) имеет второй порядок аппроксимации, т.е.

 

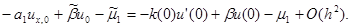Докажем последнее утверждение. Используя разложение

 

u_{x, 0} = (u₁ – u₀)/h = u’(x_1/2) + O(h²), x_1/2 = 0,5h,

a₁ = k_1/2 + O(h²)

получим

 

 

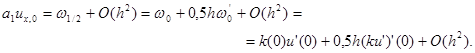Отсюда имеем

 

 

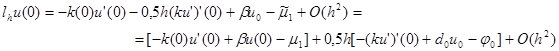Учитывая граничное условие (2), получаем

 

l_hu(0) = 0,5h [– (ku’)’(0) + d₀u₀ – j ₀ ] + O(h²).

 

Выражение, стоящее в квадратных скобках, преобразуем, учитывая уравнение (1), к виду

 

– (ku’)’(0) + d₀u₀ – j ₀ = – (ku’)’(0) + q(0)u(0) – f(0) +

                              + (d₀ – q(0))u₀ – (f(0) – j ₀ ) = (d₀ – q(0))u₀ – (f(0) – j ₀ ).

 

Из соотношений

 

 

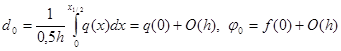получаем

 

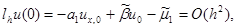что и требовалось доказать.

Таким образом, при достаточной гладкости коэффициентов k(x), q(x), f(x) и решения u(x) разностная схема (10) аппроксимирует исходную задачу (2) со вторым порядком по h.

При практическом использовании разностной схемы для нахождения ее коэффициентов не обязательно вычислять интегралы (4), (6) точно. Можно воспользоваться коэффициентами, полученными путем замены этих интегралов квадратурными формулами, имеющими точность O(h²) и выше. Например, в результате применения формулы прямоугольников получим следующие коэффициенты: a_i = k(x_i – 0,5h), d_i = q(x_i), j _i = f(x_i).

Применяя формулу трапеций, получим

 

 

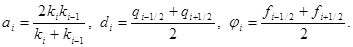Представление коэффициентов разностной схемы в виде интегралов (4), (6) оказывается полезным при исследовании сходимости в случае разрывных функций k(x), q(x), f(x).

 

2.3. Уравнение для погрешности. Решение y_i = y(x_i) разностной задачи (3), (4) зависит от шага h сетки, y(x_i) = y_h(x_i). По существу, мы имеем семейство решений {y_h(x_i)}, зависящее от параметра h. Говорят, что решение y_h(x) разностной задачи сходится к решению u(x) исходной дифференциальной задачи, если при h®0 погрешность y_h(x_i) – u(x_i), i = 0, 1,…, N, стремится к нулю в некоторой норме. В настоящем параграфе в качестве такой нормы будем брать норму в сеточном пространстве C( w _h ), т.е. положим

 

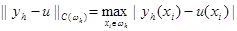Говорят, что разностная схема имеет m-й порядок точности (или сходится с порядком m), если

 

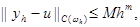где m>0, M>0 – константы, не зависящие от h.

Выше было установлено, что схема (3), (4) имеет второй порядок аппроксимации. Докажем теперь, что эта схема имеет и второй порядок точности. Для этого прежде всего выпишем уравнение, которому удовлетворяет погрешность z_i = y_i – u(x_i). Поставим y_i = z_i + u(x_i) в уравнения (3), (4). Тогда получим уравнения

 

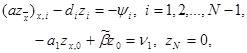(11)

(12)

где обозначено

 

 

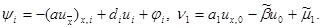Функция y _i, входящая в правую часть уравнения (11), называется погрешностью аппроксимации дифференциального уравнения (1) разностным уравнением (3) на решении задачи (1), (2). В п.1 было доказано, что y _i = O(h²) при h®0, i=1, 2,…, N–1. Аналогично, величина n₁ является по определению погрешностью аппроксимации краевого условия (2) разностным краевым условием (4) на решении задачи (1), (2), причем n ₁ =O(h²). Таким образом, структура уравнений для погрешности (11), (12) та же, что и у разностной схемы (3), (4), отличаются только правые части.

Чтобы доказать сходимость разностной схемы, оценим решение задачи (11), (12) через правые части y _i , n ₁, т.е. получим неравенство вида

 

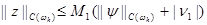                                                                                                            (13)

 

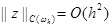с константой M₁, не зависящей от h. Из этого неравенства и будет следовать, что

 

 

Отметим, что неравенства вида (13), называемые априорными оценками, нашли широкое применение в теории разностных схем. Поскольку структура для погрешности (11), (12) та же, что и у разностной схемы (3), (4), а отличаются только правые части, то оценка (13) выполняется одновременно с аналогичной оценкой

 

 

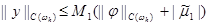для разностной схемы (3), (4) при m ₂ = 0. Последняя оценка выражает устойчивость решения разностной задачи по правым частям j и m ₁.

 

2.4. Разностные тождества и неравенства. Для того, чтобы доказать неравенство (13), нам потребуются некоторые разностные тождества и неравенства. Будем рассматривать сеточные функции, заданные на сетке (7). Обозначим

 

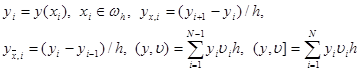Справедливо следующее разностное утверждение:

 

(y, u _x ) = –( u , y_x) + y_N u _N – y₀ u ₁ .                                                           (14)

 

Действительно,

 

 

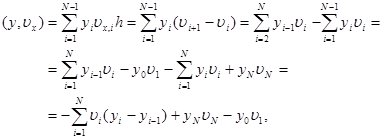что и требовалось доказать. Тождество (14) называется формулой суммирования по частям.

Подставляя в (14) вместо u выражение az_x и вместо y функцию z, получаем первую разностную формулу Грина

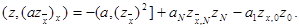(15)

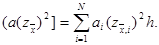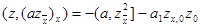Здесь                                      В частности, если z_N = 0 (как в задаче (11), (12)), то получим

(16)

 

Обозначим

 

 

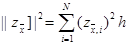и докажем, что для любой сеточной функции z_i, удовлетворяющей условию z_N = 0, справедливо неравенство

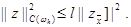(17)

 

Для доказательства воспользуемся тождеством

 

 

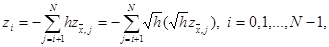и применим неравенство Коши-Буняковского

 

 

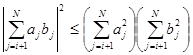Тогда получим

 

 

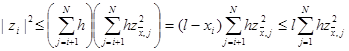Откуда сразу следует неравенство (17).

 

2.5. Доказательство сходимости. Возвращаясь к доказательству сходимости схемы (3), (4), получим тождество, которому удовлетворяет погрешность z_i = y_i – u(x_i). Для этого умножим уравнение (11) на hz_i и просуммируем по i от 1 до N–1. Тогда получим

 

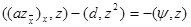Отсюда, применяя разностную формулу Грина (16), получим

 

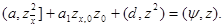Далее, согласно (12) имеем

 

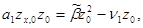следовательно, справедливо тождество

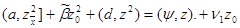(18)

 

Из этого тождества и будет сейчас выведено требуемое неравенство вида (13).

Заметим прежде всего, что если

 

k(x) ³ c₁ > 0, b ³ 0, q(x) ³ 0,

 

то коэффициенты разностной схемы (3), (4) удовлетворяют неравенствам

 

a_i ³ c₁ > 0, b ³ 0, d_i ³ 0.                                                                 (19)

 

Это утверждение сразу следует из явного представления коэффициентов (5), (6).

Воспользовавшись (19), оценим слагаемые, входящие в левую часть тождества (18), следующим образом:

 

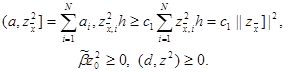Тогда придем к неравенству

 

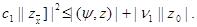(20)

 

Оценим сверху правую часть этого неравенства. Будем иметь

 

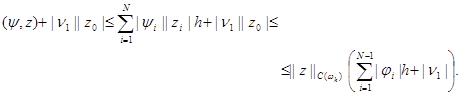Подставляя эту оценку в (20) и учитывая неравенство (17), получим

 

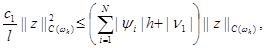т.е.

 

 

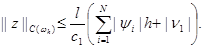Окончательно

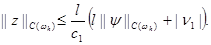(21)

Поскольку                                                                         из неравенства следует,

что погрешность z_i = y_i – u(x_i) также является величиной O(h²) при h®0. Итак, справедливо следующее утверждение.

Пусть k(x) – непрерывно дифференцируемая и q(x), f(x) – непрерывные функции при x Î [0, l], решение u(x) задачи (1), (2) обладает непрерывными четвертыми производными. Пусть коэффициенты разностной схемы (3), (4) удовлетворяют условиям (8), (9), (19). Тогда решение разностной задачи (3), (4) сходится при h ® 0 к решению исходной дифференциальной задачи (1), (2) со вторым порядком по h, так что выполняется оценка

 

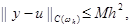где M – постоянная, не зависящая от h.