Разностные схемы для уравнения теплопроводности

3.1. Исходная задача. Будем рассматривать следующую первую краевую задачу для уравнения теплопроводности с постоянными коэффициентами. В области {0 < x < 1, 0 < t £ T} требуется найти решение уравнения

(1)

 

удовлетворяющее начальному условию

u(x, 0) = u₀(x)                                                                                      (2)

и граничным условиям

u(0, t) = m ₁ (t), u(1, t) = m ₂ (t).                                                               (3)

Здесь u0(x), m ₁ (t), m ₂ (t) – заданные функции. Известно, что при определенных предположениях гладкости решение задачи (1)–(3) существует и единственно. В дальнейшем при исследовании аппроксимации разностных схем будем предполагать, что решение u(x, t) обладает необходимым по ходу изложения числом производных по x и по t. Решение задачи (1) – (3) удовлетворяет принципу максимума и тем самым непрерывно зависит от начальных и граничных данных.

 

3.2. Явная схема. Как всегда, для построения разностной схемы надо прежде всего ввести сетку в области изменения независимых переменных и задать шаблон, т.е. множество точек сетки, участвующих в аппроксимации дифференциального выражения. Введем сетку по переменному x такую же, как в предыдущей главе, т.е.

w _h = {x_i = ih, i = 0, 1,…, N, hN = 1}

и сетку по переменному t с шагом t, которую обозначим

w _t = {t_n = n t , n = 0, 1,…, K, K t = T}

Точки (x_i, t_n), i = 0, 1,…, N, n = 0, 1,…, K, образуют узлы пространственно-временной сетки w_{h, t} = w_h x w_t. Узлы (x_i, t_n), принадлежащие отрезкам I₀ = {0 £ x £ 1, t = 0}, I₁ = {x = 0, 0 £ t £ T}, I₂ = {x = 1, 0 £ t £ T}, называются граничными узлами сетки w_{h, t}, а остальные узлы – внутренними. На рисунке граничные узлы обозначены крестиками, а внутренние – кружочками.

Слоем называется множество всех узлов сетки w_{h, t}, имеющих одну и ту же временную координату. Так, n-м слоем называется множество узлов

 

(x₀, t_n), (x₁, t_n),…, (x_N, t_n).

 

Для функции y(x, t), определенной на сетке w_{h, t}, введем обозначения yⁿ_i = y(x_i, t_n),

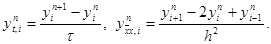(4)

 

Иногда для упрощения записи индексы i и n будем опускать, обозначая

 

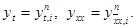
                 ( x_i, t_n+1 )                              (x_i-1, t_n+1) (x_i, t_n+1) (x_i+1, t_n+1)

(x_i-1, t_n)    (x_i, t_n)   (x_i+1, t_n)                                (x_i, t_n)

(x_i-1, t_n+1) (x_i, t_n+1) (x_i+1, t_n+1)                             (x_i, t_n+1)

(x_i-1, t_n)    (x_i, t_n)   (x_i+1, t_n)            (x_i-1, t_n)           (x_i, t_n) (x_i+1, t_n)

                                                                                    (x_i, t_n-1)

Чтобы аппроксимировать уравнение (1) в точке (x_i, t_n), введем шаблон, изображенный на рисунке и состоящий из четырех узлов (x_i±1, t_n), (x_i, t_n), (x_i, t_n+1). Производную ¶u/¶t заменим в точке (x_i, t_n) разностным отношением yⁿ_{t, i}, а производную ¶²u/¶²x – второй разностной производной yⁿ_{xx, i}. Правую часть f(x, t) заменим приближенно сеточной функцией jⁿ_i, в качестве jⁿ_i можно взять одно из следующих выражений:

 

 

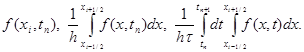В результате получим разносное уравнение

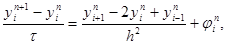(5)

 

которое аппроксимирует исходное дифференциальное уравнение в точке (x_i, t_n) с первым порядком по t и вторым порядком по h при условии, что разность j ⁿ _i – f(x_i, t_n) имеет тот же порядок малости.

Под разностной схемой понимается совокупность разностных уравнений, аппроксимирующих основное дифференциальное уравнение во всех внутренних узлах сетки и дополнительные (начальные и граничные) условия – в граничных узлах сетки. Разностную схему по аналогии с дифференциальной задачей будем называть также разностной задачей. В данном случае разностная схема имеет вид

 

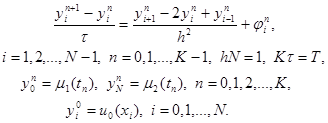(6)

 

 

Эта схема представляет собой систему линейных алгебраических уравнений с числом уравнений, равным числу неизвестных. Находить решение такой системы следует по слоям. Решение на нулевом слое задано начальными условиями y⁰_i = u₀(x_i), i = 0, 1,…, N. Если решение yⁿ_i, i = 0, 1,…, N, на слое n уже найдено, то решение y_iⁿ⁺¹ на слое n+1 находится по явной формуле

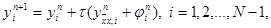(7)

 

а значения                                                             доопределяются из граничных

условий. По этой причине схема (6) называется явной разностной схемой. Несколько позже мы познакомимся и с неявными схемами, в которых для нахождения y_iⁿ⁺¹ при заданных y_iⁿ требуется решать систему уравнений.

Погрешность разностной схемы (6) определяется как разность z_iⁿ = y_iⁿ – u(x_i, t_n) между решением задачи (6) и решением исходной задачи (1) – (3). Подставляя в (6) y_iⁿ = z_iⁿ + u(x_i, t_n), получим уравнение для погрешности

 

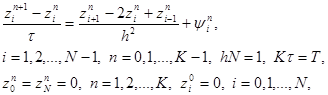(8)

 

где                                                     – погрешность аппроксимации разностной

схемы (6) на решении задачи (1) – (3), y _i ⁿ = O( t + h²). Можно оценить решение z_iⁿ уравнения (8) через правую часть y_iⁿ и доказать тем самым сходимость разностной схемы (6) с первым порядком по t и вторым – по h. Однако это исследование мы отложим, а сейчас на примере схемы (6) продемонстрируем один распространенный прием исследования разностных схем с постоянными коэффициентами, называемый методом гармоник. Хотя данный метод не является достаточно обоснованным, в частности не учитывает влияния граничных условий и правых частей, он позволяет легко найти необходимые условия устойчивости и сходимости разностных схем. Покажем, например, что явную схему (6) можно применять лишь при условии t £ 0,5h², означающем, что шаг по времени надо брать достаточно малым.

Рассмотрим уравнение

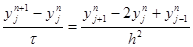(9)

 

т.е. однородное уравнение, соответствующее (5). Будем искать частные решения (9), имеющие вид

y_jⁿ ( j ) = qⁿe^{ijh j},                                                                                    (10)

 

где i – мнимая единица, j – любое действительное число и q – число, подлежащее определению. Подставляя (10) в уравнение (9) и сокращая на e^{ijh j}, получим

 

 

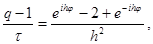откуда найдем

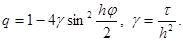(11)

Начальные условия                           соответствующие решениям вида (10) (их называют гармониками), ограничены. Если для некоторого j множитель q станет по модулю больше единицы, то решение вида (10) будет неограниченно возрастать при n®¥. В этом случае разностное уравнение (9) называется неустойчивым, поскольку нарушается непрерывная зависимость его решения от начальных условий. Если же |q| £ 1 для всех действительных j, то все решения вида (10) ограничены при любом n и разностное уравнение (9) называется устойчивым. В случае неустойчивости найти решение разностной задачи (6) по формулам (7) практически невозможно, так как погрешности (например погрешности округления), внесенные в начальный момент времени, будут неограниченно возрастать при увеличении n. Такие разностные схемы называются неустойчивыми.

Для уравнения (9) неравенство |q| £ 1 выполняется согласно (11) при всех j тогда и только тогда, когда g £ 0,5. Таким образом, использование схемы (6) возможно лишь при выполнении условия t £ 0,5h². Разностные схемы, устойчивые лишь при некотором ограничении на отношение шагов по пространству и по времени, называются условно устойчивыми. Следовательно, схема (6) возможно устойчива, причем условие устойчивости имеет вид t/h² £ 0,5. Условно устойчивые схемы для уравнений параболического типа используются редко, так как они накладывают слишком сильное ограничение на шаг по времени. Действительно, пусть, например, h = 10^-2. Тогда шаг t не должен превосходить 0,5 * 10^-4, и для того чтобы вычислить решение y_jⁿ при t = 1, надо взять число шагов по времени n = t^-1 ³ 2 * 10⁴, т.е. провести не менее 2 * 10⁴ вычислений по формулам (7).

 

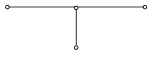
3.3. Неявные схемы. Чисто неявной разностной схемой для уравнения теплопроводности теплопроводности (схемой с опережением) называется разностная схема, использующая шаблон (x_i, t_n), (x_{i ± 1} , t_n+1), (x_i, t_n+1) и имеющая вид

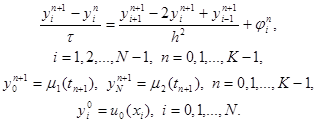(12)

 

Здесь j ⁿ _i = f(x_i, t_n+1) + O( t + h²). Схема имеет первый порядок аппроксимации по t и второй – по h. Решение системы (12) находится, как и в случае явной схемы, по слоям, начиная с n = 1. Однако, теперь, в отличие от явной схемы, для нахождения yⁱ_n+1 по известным y_iⁿ требуется решить систему уравнений

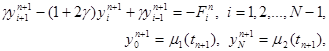(13)

 

где g = t /h², F_iⁿ = y_iⁿ + t j _i ⁿ. Эту систему можно решать методом прогонки, так как условия устойчивости прогонки выполнены.

Для исследования устойчивости разностной схемы (12) будем искать частные решения уравнения

 

 

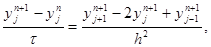имеющие вид (10). Тогда получим

 

 

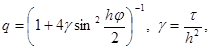следовательно, |q| £ 1 при любых j , t , h. Таким образом, схема (12) абсолютно устойчива, т.е. устойчива при любых шагах t и h. Абсолютная устойчивость является основным условием неявных схем. Теперь уже не надо брать шаг t слишком малым, можно взять, например, t = h = 10^-2. Величина шагов сетки t , h определяются теперь необходимой точностью расчета, а не соображениями устойчивости.

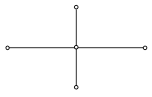
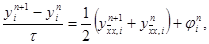Шеститочечной симметричной схемой называется разностная схема

(14)

 

 

для которой начальные и граничные условия задаются так же, как и в схеме (12). Эта схема использует шеститочечный шаблон, изображенный на рисунке.

Обобщением трех рассмотренных схем является однопараметрическое семейство схем с весами. Зададим произвольный действительный параметр s и определим разностную схему

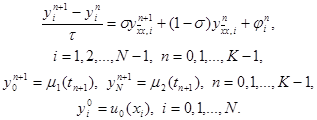(15)

 

 

При s = 0 получим отсюда явную схему, при s = 1 – чисто неявную схему и при s = 0,5 – симметричную схему (14). Исследуем погрешность аппроксимации схемы (15) на решении исходной задачи (1) – (3). Представим решение задачи (15) в виде y_iⁿ = u(x_i, t_n) + z_iⁿ, где u(x_i, t_n) – точное решение дифференциальной задачи (1) – (3). Тогда для погрешности получим систему уравнений

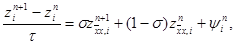(16)

 

i = 1, 2,…, N – 1, n = 0, 1,…, K – 1,

z₀ⁿ⁺¹ = z_Nⁿ⁺¹ = 0, n = 0, 1,…, K – 1, z_i⁰ = 0, i = 0, 1,…, N.

 

Сеточная функция y_iⁿ, входящая в правую часть уравнения (16) и равная

 

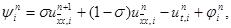(17)

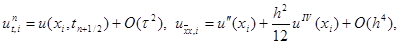называется погрешностью аппроксимации схемы (15) на решении задачи (1) – (3). Получим первые члены разложения функции y_iⁿ по степеням h и t. Будем разлагать все функции, входящие в выражение для y_iⁿ, по формуле Тейлора в точке (x_i, t_n + 0,5t). Учитывая разложения

 

 

где

 

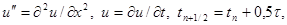получим

 

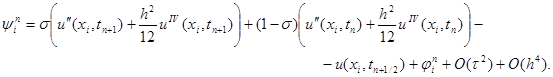Отсюда, проводя разложение в точке (x_i, t_n+1/2) и обозначая u = u (x_i, t_n+1/2), будем иметь

 

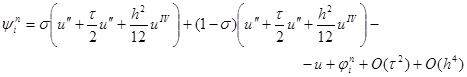и, перегруппировывая слагаемые, получим, что

 

 

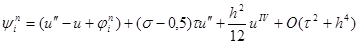Учитывая уравнение (1) u’’ – u = – f и следствие из него u^IV – u’’ = –f’’, окончательно можно записать, что

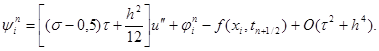(18)

 

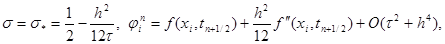Из формулы (18) можно сделать следующие выводы. Если

 

 

то схема (15) имеет второй порядок аппроксимации по t и четвертый – по h. Такая схема называется схемой повышенного порядка аппроксимации. Если

 

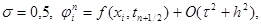то схема (15) имеет второй порядок аппроксимации по t и по h. При остальных значениях s и при j _i ⁿ º 0 в виде (10), то получим

 

 

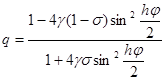и |q| £ 1 при всех j, если

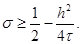(19)

 

Отсюда видно, в частности, что все схемы с s ³ 0,5 абсолютно устойчивы. Схема повышенного порядка аппроксимации (s = s_*) также абсолютно устойчива, что проверяется непосредственно.

При s ¹ 0 разностная схема (15) является неявной схемой. Для нахождения решения y_iⁿ⁺¹ по заданным y_iⁿ требуется решать систему уравнений

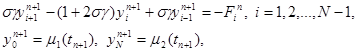(20)

 

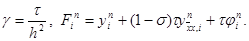где

 

 

Система (20) решается методом прогонки. Условия устойчивости прогонки при s ¹ 0 сводятся к неравенству

 

|1 + 2 s g | ³ 2 | s | g

 

и выполнены при s ³ – 1/(4g). Последнее неравенство следует из условия устойчивости (19) разностной схемы.

 

3.4. Уравнения с переменными коэффициентами и линейные уравнения. Рассмотрим первую краевую задачу для уравнения теплопроводности с переменными коэффициентами

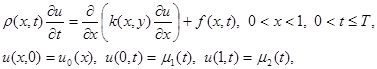(21)

 

 

где r (x, t), k(x, t), f(x, t) – достаточно гладкие функции, удовлетворяющие условиям

 

0 < c₁ £ k(x, t) £ c₂, r (x, t) ³ c₃ > 0.                                                  (22)

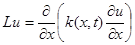Дифференциальное выражение                                                          при каждом

фиксированном t аппроксимируем в точке (x_i, t) так же, как и в стационарном случае, разностным отношением

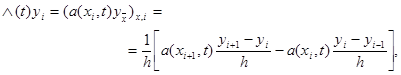(23)

 

 

где разностный коэффициент теплопроводности a(x_i, t) должен удовлетворять условиям второго порядка аппроксимации

 

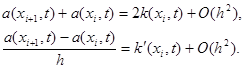Наиболее употребительны следующие выражения для a(x_i, t):

 

 

Разностная схема с весами для задачи (21) имеет вид

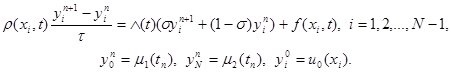(24)

 

 

Здесь в качестве t можно взять любое значение t Î [t_n, t_n+1], например t = t_n + 0,5 t. Если в уравнении (24) t = t_n + 0,5 t , s = 0,5, то схема (24) имеет второй порядок аппроксимации по t и по h. При остальных значениях s и t выполняется первый порядок аппроксимации по t и второй – по h.

При исследовании устойчивости разностных схем с переменными коэффициентами иногда применяется принцип замороженных коэффициентов, сводящий задачу к уравнению с постоянными коэффициентами. Рассмотрим явную схему, соответствующую уравнению (24) с s = 0 и f(x_i, t) º 0, т.е. схему

(25)

 

Предположим, что коэффициенты r (x_i, t), a(x_i, t) – постоянные, r (x_i, t) º r = const, a(x_i, t) º a = const. Тогда уравнение (25) можно записать в виде

 

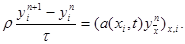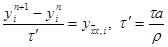или

 

 

Из п.2 известно, что последнее уравнение устойчиво при t ’ £ 0,5h², т.е. при

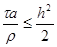(26)

 

Принцип замороженных коэффициентов утверждает, что схема (25) устойчива, если условие (26) выполнено при всех допустимых значениях a(x_i, t), r (x_i, t), т.е. если при всех x, t выполнены неравенства

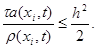(27)

 

Если известно, что 0 < c₁ £ a(x_i, t) £ c₂, r (x_i, t) ³ c₃ > 0, то неравенство (27) будет выполнено при

 

 

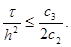Строгое обоснование устойчивости схемы (25) будет дано в примере 2 из главы 2.

Если параметр s ³ 0,5, то из принципа замороженных коэффициентов следует абсолютная устойчивость схемы (24).

Рассмотрим теперь первую краевую задачу для нелинейного уравнения теплопроводности

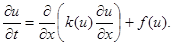(28)

 

В случае нелинейных уравнений, когда заранее неизвестны пределы изменения функции k(u), избегают пользоваться явными схемами. Чисто неявная схема, линейная относительно y_iⁿ⁺², i = 1, 2,…, N – 1, имеет вид

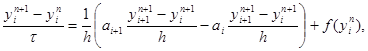(29)

 

где a_i = 0,5 (k(yⁿ_i) + k(yⁿ_i-1)). Эта схема абсолютно устойчива, имеет первый порядок аппроксимации по t и второй – по h. Решение y_iⁿ⁺¹, i = 1, 2,…, N – 1, находится методом прогонки. Заметим, что схему (29) можно записать в виде

 

 

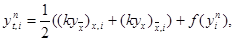где k_i = k(y_iⁿ).

Часто используется нелинейная схема

 

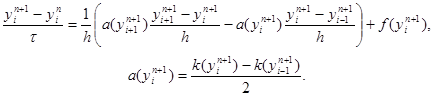(30)

 

 

Для реализации этой схемы необходимо применить тот или иной итерационный метод. Например такой:

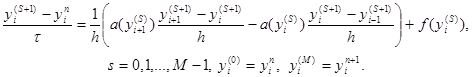
(31)

 

 

Здесь s – номер итерации. Как видим, нелинейные коэффициенты берутся с предыдущей итерации, а в качестве начального приближения для y_iⁿ⁺¹ выбирается y_iⁿ. Это начальное приближение тем лучше, чем меньше шаг t. Число итераций M задается из соображений точности. В задачах с гладкими коэффициентами при k(u) ³ c₁ > 0 часто бывает достаточно провести две – три итерации. Значения y_i^(S+1) на новой итерации находятся из системы (31) методом прогонки. При M = 1 итерационный метод (31) совпадает с разностной схемой (29).

Для приближенного решения нелинейного уравнения (28) применяются также схемы предиктор – корректор второго порядка точности, аналогичные методу Рунге – Кутта для обыкновенных дифференциальных уравнений. Здесь переход со слоя n на слой n+1 осуществляется в два этапа. Приведем пример такой схемы. На первом этапе решается неявная линейная система уравнений

 

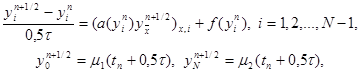из которой находятся промежуточные значения y_i^n+1/2, i = 0, 1,…, N. Затем на втором этапе используется симметричная шеститочечная схема для уравнения (28), в которой нелинейные коэффициенты a(y), f(y) вычисляются при y = y_i^n+1/2, т.е. схема