 |
Главная |
Приведение задачи к канонической форме
|
из
5.00
|
Содержание
| 1. Постановка задачи 1.1. Физическая постановка задачи 1.2. Математическая постановка задачи 2. Приведение задачи к канонической форме 3. Нахождение начального опорного плана с помощью L-задачи 3.1. Постановка L-задачи 3.2. Решение L-задачи 3.3. Формирование начального опорного плана исходной задачи линейного программирования из оптимального плана L-задачи 4. Решение исходной задачи I алгоритмом симплекс-метода 5. Формирование М-задачи 6. Решение М-задачи вторым алгоритмом симплекс-метода 7. Формирование двойственной задачи 8. Формирование оптимального решения двойственной задачи на основе теоремы о двойственности 9. Анализ результатов и выводы |
Постановка задачи
Физическая (техническая) постановка задачи
Нефтеперерабатывающий завод получает четыре полуфабриката:
- 400 тыс. л. алкилата;
- 250 тыс. л. крекинг-бензина;
- 350 тыс. л. бензина прямой перегонки;
- 250 тыс. л. изопентона;
В результате смешивания этих четырёх компонентов в разных пропорциях образуются три сорта авиационного бензина:
- Бензин А – 2 : 3 : 5 : 2 ;
- Бензин В – 3 : 1 : 2 : 1 ;
- Бензин С – 2 : 2 : 1 : 3 ;
Стоимость 1 тыс.л. указанных сортов бензина:
- Бензин А – 120 руб.
- Бензин Б – 100 руб.
- Бензин С – 150 руб.
Необходимо определить план смешения компонентов, при котором будет достигнута максимальная стоимость все продукции. При следующих условиях:
- Бензина каждого сорта должно быть произведено не менее 300 тыс..л.
- Неиспользованного крекинг бензина должно остаться не более 50 тыс.л.
Сводная таблица условий задачи:
|
Компоненты, используемые для производства трёх видов бензина. | Сорта производимого бензина | Объем ресурсов (тыс. л) | ||
| А | В | С | ||
| Алкилат | 
| 
| 
| 400 |
| Крекинг-бензин | 
| 
| 
| 250 |
| Бензин прямой перегонки | 
| 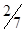
| 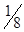
| 300 |
| Изопентат | 
| 
| 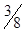
| 250 |
| Цена бензина (рублей за 1 тыс.л.) | 120 | 100 | 150 | |
Математическая постановка задачи
Исходя из условий задачи, необходимо максимизировать следующую целевую функцию:
 (1.2.1)
(1.2.1)
При ограничениях
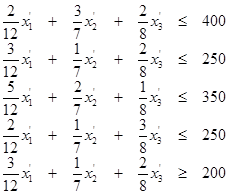 (1.2.2)
(1.2.2)
 , где
, где 
В этих выражениях:
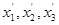 - объемы бензина А-го, В-го и С-го сорта соответственно.
- объемы бензина А-го, В-го и С-го сорта соответственно.
Тогда
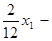 объёмная доля первой компоненты (алкилата) в бензине А.
объёмная доля первой компоненты (алкилата) в бензине А.
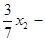 объёмная доля первой компоненты (алкилата) в бензине В.
объёмная доля первой компоненты (алкилата) в бензине В.
 объёмная доля первой компоненты (алкилата) в бензине С.
объёмная доля первой компоненты (алкилата) в бензине С.
и т.д.
Целевая функция  выражает стоимость всей продукции в зависимости от объема производимого бензина каждого сорта. Таким образом, для получения максимальной стоимости продукции необходимо максимизировать целевую функцию
выражает стоимость всей продукции в зависимости от объема производимого бензина каждого сорта. Таким образом, для получения максимальной стоимости продукции необходимо максимизировать целевую функцию  (1.2.1) с соблюдением всех условий задачи, которые накладывают ограничения (1.2.2) на
(1.2.1) с соблюдением всех условий задачи, которые накладывают ограничения (1.2.2) на  .
.
Приведение задачи к канонической форме
Задача линейного программирования записана в канонической форме, если она формулируется следующим образом.
Требуется найти вектор  , доставляющий максимум линейной форме
, доставляющий максимум линейной форме
 (2.1)
(2.1)
при условиях
 (2.2)
(2.2)
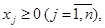 (2.3)
(2.3)
где 
Перепишем исходную задачу (1.2.1) - (1.2.2):
 (2.4)
(2.4)
При ограничениях
 (2.5)
(2.5)
 , где
, где  (2.6)
(2.6)
В канонической форме задачи линейного программирования необходимо, чтобы все компоненты искомого вектора Х были неотрицательными, а все остальные ограничения записывались в виде уравнений. Т.е. в задаче обязательно будут присутствовать условия вида (2.3) и 8 уравнений вида (2.2), обусловленных неравенствами (2.5), (2.6).
Число ограничений задачи, приводящих к уравнениям (2.2) можно уменьшить, если перед приведением исходной задачи (2.4) - (2.6) к канонической форме мы преобразуем неравенства (2.6) к виду (2.3). Для этого перенесем свободные члены правых частей неравенств (2.6) в левые части. Таким образом, от старых переменных  перейдем к новым переменным
перейдем к новым переменным 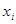 , где
, где  :
:
 ,
,  .
.
Выразим теперь старые переменные через новые
 ,
,  (2.7)
(2.7)
и подставим их в линейную форму (2.4) и в неравенства (2.5), (2.6). Получим


 , где
, где  .
.
Раскрывая скобки и учитывая, что
 (2.8),
(2.8),
можем окончательно записать:
 (2.9)
(2.9)
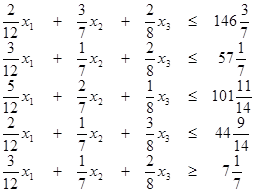 (2.10)
(2.10)
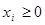 , где
, где  (2.11)
(2.11)
Путем несложных преобразований задачу (1.2.1), (1.2.2) свели к задаче (2.9) - (2.11) с меньшим числом ограничений.
Для записи неравенств (2.10) в виде уравнений введем неотрицательные дополнительные переменные  , и задача (2.9) - (2.11) запишется в следующей эквивалентной форме:
, и задача (2.9) - (2.11) запишется в следующей эквивалентной форме:
 (2.12)
(2.12)
 (2.13)
(2.13)
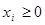 , где
, где 
Задача (2.12), (2.13) имеет каноническую форму.
3. Нахождение начального опорного плана с помощью L -задачи
Начальный опорный план задачи (2.1) - (2.3), записанной в канонической форме, достаточно легко может быть найден с помощью вспомогательной задачи (L-задачи):
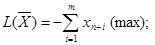 (3.1)
(3.1)
 (3.2)
(3.2)
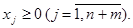 (3.3)
(3.3)
Начальный опорный план задачи (3.1) - (3.3) известен. Он состоит из компонент

и имеет единичный базис Б =  = E .
= E .
Решая вспомогательную задачу первым алгоритмом симплекс-метода (описание алгоритма приводится в п.4), в силу ограниченности линейной формы 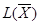 сверху на множестве своих планов (
сверху на множестве своих планов (  ) получим, что процесс решения через конечное число шагов приведет к оптимальному опорному плану вспомогательной задачи.
) получим, что процесс решения через конечное число шагов приведет к оптимальному опорному плану вспомогательной задачи.
Пусть  - оптимальный опорный план вспомогательной задачи. Тогда
- оптимальный опорный план вспомогательной задачи. Тогда  является опорным планом исходной задачи. Действительно, все дополнительные переменные
является опорным планом исходной задачи. Действительно, все дополнительные переменные  . Значит,
. Значит,  удовлетворяет условиям исходной задачи, т.е. является некоторым планом задачи (2.12) - (2.13). По построению план
удовлетворяет условиям исходной задачи, т.е. является некоторым планом задачи (2.12) - (2.13). По построению план  является также опорным.
является также опорным.
Постановка L -задачи
Вспомогательная задача для нахождения начального опорного плана задачи (2.12) - (2.13) в канонической форме состоит в следующем.
Требуется обратить в максимум

при условиях

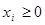 , где
, где 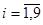 .
.
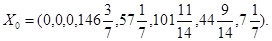 |
рассматривая в качестве исходного опорного плана план
Здесь добавление только одной дополнительной переменной  (вместо пяти) обусловлено тем, что исходная задача уже содержит четыре единичных вектора условий А4, А5, А6, А7.
(вместо пяти) обусловлено тем, что исходная задача уже содержит четыре единичных вектора условий А4, А5, А6, А7.
Решение L -задачи
Решение L-задачи будем проводить в соответствии с первым алгоритмом симплекс-метода (описание алгоритма приводится в п.4). Составим таблицу, соответствующую исходному опорному плану (0-й итерации).
Т.к. Б0 =  - базис, соответствующий известному опорному плану
- базис, соответствующий известному опорному плану  , является единичной матрицей, то коэффициенты разложения векторов Аj по базису Б0
, является единичной матрицей, то коэффициенты разложения векторов Аj по базису Б0
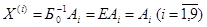 .
.
Значение линейной формы  и оценки
и оценки  для заполнения (m+1)-й строки таблицы определяются следующими соотношениями:
для заполнения (m+1)-й строки таблицы определяются следующими соотношениями:
 ,
,
 .
.
Отсюда получим:
 ;
;
 ;
;
 ;
;
…
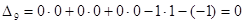 .
.
Весь процесс решения задачи приведен в табл. 3.2.1, которая состоит из 2 частей, отвечающих 0-й (исходная таблица) и 1-й итерациям.
Заполняем таблицу 0-й итерации.
Среди оценок  имеются отрицательные. Значит, исходный опорный план не является оптимальным. Перейдем к новому базису. В базис будет введен вектор А1 с наименьшей оценкой
имеются отрицательные. Значит, исходный опорный план не является оптимальным. Перейдем к новому базису. В базис будет введен вектор А1 с наименьшей оценкой  . Значения t вычисляются для всех позиций столбца t (т.к. все элементы разрешающего столбца положительны). Наименьший элемент
. Значения t вычисляются для всех позиций столбца t (т.к. все элементы разрешающего столбца положительны). Наименьший элемент  достигается на пятой позиции базиса. Значит, пятая строка является разрешающей строкой, и вектор А9 подлежит исключению из базиса.
достигается на пятой позиции базиса. Значит, пятая строка является разрешающей строкой, и вектор А9 подлежит исключению из базиса.
Составим таблицу, отвечающую первой итерации.
В столбце Бх, в пятой позиции базиса место вектора А9 занимает вектор А1. Соответствующий ему коэффициент линейной формы С41 = 0 помещаем в столбец Сх. Главная часть таблицы 1 заполняется по данным таблицы 0 в соответствии с рекуррентными формулами. Так как все  , то опорный план
, то опорный план 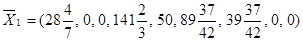 является решением L-задачи. Наибольшее значение линейной формы равно
является решением L-задачи. Наибольшее значение линейной формы равно  .
.
Таблица 3.2.1

3.3. Формирование начального опорного плана исходной задачи линейного программирования из оптимального плана L -задачи
Поскольку 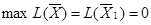 , где
, где 
 - оптимальный опорный план L-задачи, то
- оптимальный опорный план L-задачи, то 
 является начальным опорным планом исходной задачи (2.12) - (2.13).
является начальным опорным планом исходной задачи (2.12) - (2.13).
|
из
5.00
|
Обсуждение в статье: Приведение задачи к канонической форме |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

