Формирование двойственной задачи

Произвольной задаче линейного программирования определенным образом соответствует некоторая другая задача линейного программирования. Будем называть ее двойственной, а первоначальную задачу – исходной.

Обозначим

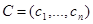; ; ; ; (7.1)

Теперь исходная задача (2.1) - (2.3) в канонической форме может быть записана в матричном виде следующим образом.

Требуется определить вектор , обращающий в максимум

.                                                                                                (7.2)

при условиях

AX=B;                                                                                                          (7.3)

.                                                                                                         (7.4)

Тогда двойственная задача – определить вектор , обращающий в минимум

f(Y)=YB                                                                                                        (7.5)

при условиях

.                                                                                                        (7.6)

Транспонируя обе части неравенства (7.6), записанного в виде строки, и учитывая , получим

.                                                                                                 (7.7)

Отметим, что в двойственной задаче переменные y_i могут быть и отрицательными.

Рассмотрим в качестве исходной задачу (2.12), (2.13). С учетом (7.1) и (7.7) запишем

С = (120, 100, 150, 0, 0, 0, 0, 0), B = ( , , , , ),

.

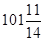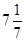Двойственная задача имеет вид

;    (7.8)

         (7.9)

8. Формирование оптимального решения двойственной задачи на основе теоремы о двойственности

Оказывается, что для задач (7.2) - (7.4) и (7.5), (7.6), называемых двойственной парой, справедлива следующая теорема.

Теорема (первая теорема о двойственности). Если одна из задач двойственной пары (7.2) - (7.4) и (7.5), (7.6) имеет решение, то другая задача также разрешима. При этом для любых оптимальных планов  и 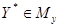(здесь М_х, М_у – множества планов соответственно прямой и двойственной задач) задач (7.2) - (7.4) и (7.5), (7.6) имеет место равенство

.                                                                           

Если линейная форма одной из задач не ограничена (для F(X) – сверху, для f(Y) - снизу), то другая задача не имеет ни одного плана.

Оптимальное решение двойственной задачи может быть найдено на основе следующего следствия из этой теоремы.

Следствие. Если вектор  является оптимальным опорным планом задачи (7.2) - (7.4), то вектор (8.1), является оптимальным опорным планом задачи (7.5), (7.6).

Стоит отметить, что в ходе решения исходной задачи вторым алгоритмом, при каждом шаге вычисляется вектор 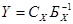. И если Х – оптимальный опорный план задачи (7.2) - (7.4), то в (m+1)-й строке, соответствующей основной таблице, находится решение задачи (7.5), (7.6).

Пусть двойственная задача имеет вид (7.8), (7.9).

Так как исходная задача (2.12), (2.13) имеет решение, то на основании рассмотренной теоремы о двойственности двойственная задача также разрешима.

Оптимальным опорным планом исходной является  (см. п.4, п.6). При этом

;            

; .

Вычислим

.

На основании следствия из теоремы о двойственности можно заключить, что  является оптимальным планом двойственной задачи, при котором . Анализируя (m+1)-ю строку основной таблицы (см. табл. 6.3, шаг 5), можно убедиться в том, что оптимальный план двойственной задачи, сформированный на основе теоремы о двойственности, совпадает с оптимальным планом, найденном при решении исходной задачи вторым алгоритмом симплекс-метода. Это говорит о том, что оптимальный план задачи (7.8) - (7.9) найден верно.