 |
Главная |
Методические указания к решению задачи 1
|
из
5.00
|
 Для позиционного электропривода траектория рабочего органа может быть произвольной, а задается начальное и конечное положение и точность позиционирования. Тип траектории выбирается обычно из минимума времени отработки заданного перемещения и ограничения на максимальное значение скорости wmax и ускорения εmax. Оптимальная по быстродействию тахограмма для позиционного электропривода имеет трапецеидальный вид [1]:
Для позиционного электропривода траектория рабочего органа может быть произвольной, а задается начальное и конечное положение и точность позиционирования. Тип траектории выбирается обычно из минимума времени отработки заданного перемещения и ограничения на максимальное значение скорости wmax и ускорения εmax. Оптимальная по быстродействию тахограмма для позиционного электропривода имеет трапецеидальный вид [1]:
1 – имеет зону движения с постоянной скоростью ω* = const.
2 – треугольная тахограмма без зоны движения с постоянной скоростью.
Для кривой 1 выполняется соотношение:
 ,
,
где Qзм – заданное угловое перемещение.
В условиях задачи задана трапецеидальная тахограмма движения, тогда

Предельную скорость шагового электропривода ωзmax = ω* можно рассчитать, используя соотношение:
ω* = α [рад]* fпр [Гц],
т.е. для α° = 1° ; fпр = 1кГц



при заданном угловом перемещении ∆φ = 1000 рад.
Из тахограммы движения с постоянной скоростью можно получить:

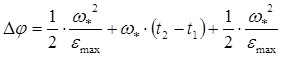 ,
,
откуда  – время движения с постоянной скоростью;
– время движения с постоянной скоростью;
tк = t1 + (t2 – t1) + (tк – t2) – полное время кадра.
Время разгона t1 = (tк – t2) = ω* / εmax .
При решении задачи выберите необходимое εmax для обеспечения
t2 – t1 > 0, так, чтобы суммарное время не превосходило время отработки кадра tк.
Путь, пройденный на участке пуска и торможения, можно определить из соотношения: 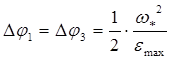 ,
,
а на участке движения с постоянной скоростью:
 .
.
При этом 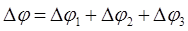
Количество импульсов управления, необходимое для выдачи на каждом из участков, равно:
 ,
,
где α – шаг двигателя.
Частота выдачи импульсов определяется так:

Для работоспособности привода частота выдачи импульсов на всех участках пуска, движения с постоянной скоростью и торможения не должна превышать частоты приемистости шагового электропривода. В случае невозможности отработки заданной траектории в соответствии с параметрами вашего задания, предложить вариант его изменения для обеспечения отработки заданного перемещения ∆φ в установленное время.
Задача 2. Составить алгоритм метода оценочной функции при осуществлении линейной интерполяции по координатам α,β для выхода в точку А с координатами (αк,βк). Построить фактическую траекторию отработки перемещения и нарисовать тактовую диаграмму подачи импульсов на соответствующие координаты. Расчетные данные свести в таблицу 7.
Таблица 7
| Номер шага I | Шаг по осям | Текущие значения | Значение оценочной функции Fi | ||
| α | β | αi | βi | ||
Данные для расчетов представлены в таблице 8.
Таблица 8
| Номер последней цифры шифра | αк | βк |
| 0 | 10 | 6 |
| 1 | 8 | 4 |
| 2 | 12 | 8 |
| 3 | 10 | 8 |
| 4 | 12 | 6 |
| 5 | 14 | 8 |
| 6 | 10 | 4 |
| 7 | 10 | 5 |
| 8 | 8 | 6 |
| 9 | 12 | 10 |
Расчеты произвести для обычного и усовершенствованного алгоритма оценочной функции. Дискретность по координатам α и β одинакова и составляет hα = hβ = 1мм/имп.
Методические указания к решению задачи 2
В большинстве систем ЧПУ одной из основных задач является обеспечение движения инструмента относительно детали по заданной траектории. Траектория движения аппроксимируется набором отрезков прямых и окружностей. Расчёт текущих значений координат при решении геометрической задачи управления называется интерполяцией.
Дискретность перемещения по координатам hx, hy, hz определяется конструкцией станка и составляет единицы или десятки мкм.
Задание приращений по двум осям координат при hx = hy еще не определит заданного прямолинейного движения инструмента между точками.
Если координаты существенно неравны (например, х = 13мм, y = 5мм при hx = hy = 0,01 мм), то по одной координате в кадре необходимо выдать 1300 импульсов, а по другой - 500. При этом время движения по оси Х не будет равно времени движения поY и заданная траектория будет искажена (как показано на рисунке).

Если по технологии недопустимо отклонение от заданной траектории (∆ велико), то приблизить фактическую траекторию к заданной можно введением дополнительных опорных точек или применять алгоритмы интерполяции.
Алгоритмы интерполяции можно разделить на алгоритмы единичных приращений: метод цифро-дифференциальных анализаторов, оценочной функции и алгоритмы равных времен: методы цифрового интегрирования, итерационно-табличные методы, прогноза и коррекции [4;6].
По алгоритму оценочной функции следует с определенной частотой, зависящей от скорости перемещения, анализировать знак оценочной функции и в зависимости от него выдавать сигнал изменения на один квант по одной или другой координате. Согласно этому методу моделируется алгебраическое уравнение воспроизводимой кривой. Оценочная функция при линейной интерполяции имеет вид:
Fi = yi·X - xi·Y,
где  ,
,  – требуемые перемещения в кадре.
– требуемые перемещения в кадре.
При проведении интерполяции осуществляют либо обычный алгоритм, либо – усовершенствованный. При обычном алгоритме расчеты значений оценочной функции осуществляют так:
- если сделан шаг по оси Х, то
Fi+1 = yi·X – (xi + 1)·Y = yi·X – xi·Y – Y = Fi – Y,
- если сделан шаг по оси Y
Fi+1 = (yi + 1)·X – xi·Y = yi·X + X – xi·Y = Fi + X.
При усовершенствованном алгоритме:
- если сделан шаг одновременно вдоль оси Х и Y
Fi+1 = (yi + 1)·X – (xi + 1)·Y = yi·X + X – xi·Y – Y = Fi + X – Y.
Таким образом, вычисление нового значения оценочной функции опирается на сохраняемые предыдущие значения.

Пример.
Пусть необходимо осуществить приращение в кадре в абстрактных машинных единицах ∆α = 6; ∆β = 4. Расчетные значения сведены в таблицу 9.
Таблица 9
| Такт i | Шаг по осям | Текущее значение | Оценочная функция | ||
| α | β | αi | βi | Fi = Fi – Δβ ≥ 0 (α) Fi = Fi + ∆α – Δβ < 0 (α и β) | |
| 0 | - | - | 0 | 0 | F0 = 0 |
| 1 | 1 | - | 1 | 0 | F1 = 0 – 4 = - 4 |
| 2 | 1 | 1 | 2 | 1 | F2 = - 4 + 6 – 4 = - 2 |
| 3 | 1 | 1 | 3 | 2 | F3 = - 2 + 6 – 4 = 0 |
| 4 | 1 | 0 | 4 | 2 | F4 = 0 – 4 = - 4 |
| 5 | 1 | 1 | 5 | 3 | F5 = - 4 + 6 – 4 = - 2 |
| 6 | 1 | 1 | 6 | 4 | F6 = - 2 + 6 – 4 = 0 |
При расчете использован усовершенствованный алгоритм, фактическая траектория движения и тактовая диаграмма показана на рисунке.

Погрешность отработки траектории по методу оценочной функции не превышает значения дискретности перемещения по координате для станка с ЧПУ. Важным достоинством метода оценочной функции является простота стыковки с шаговыми и сервоприводами и небольшая требуемая разрядность системы ЧПУ, определяемая максимальным значением координатных перемещений. Недостатком является небольшая контурная скорость:
 ,
,
где h – дискретность перемещения по координате;
Тк – время реализации алгоритма (период квантования);
к – число одновременно работающих координат.
Задача 3. Используя метод оценочной функции при круговой интерполяции, построить интерполяционную траекторию при движении из точки с координатами А0 (10, 0) в точку Ак (0, 10).
|
из
5.00
|
Обсуждение в статье: Методические указания к решению задачи 1 |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

