 |
Главная |
Методические указания к решению задачи 3
|
из
5.00
|
Наиболее универсальным способом коррекции цифровых систем управления является использование цифрового регулятора. По сравнению с аналоговым, цифровой регулятор в состоянии обеспечить лучшее качество системы управления. Введение производной в закон управления (дифференциальная составляющая) не только уменьшает перерегулирование, но и сокращает время нарастания (т. е. увеличивает быстродействие) выходного сигнала.
Интегральная составляющая позволяет устранять установившуюся ошибку, но увеличивает перерегулирование.
Пропорциональная составляющая определяет время нарастания выходной переменной.
В зависимости от характера объекта регулирования и требуемых законов управления можно использовать разные типы регуляторов.
Написание программы типового регулятора можно разделить на следующие этапы:
1. Выбор требуемого регулятора в соответствии с алгоритмом функционирования цифрового электропривода.
2. Представление модели цифрового корректирующего устройства (регулятора) в виде разностного уравнения.
3. Составление алгоритма и программы с использованием аппаратно-программных средств используемой микропроцессорной системы управления.
Пример. Непрерывный И-регулятор описывается уравнением
 ,
,
где Т и – постоянная интегрирования.

Продифференцируем исходное уравнение

и учитывая, что

dt = Tk – период квантования, получим
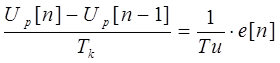
и разностное уравнение цифрового И-регулятора имеет вид:

Аналогичный результат можно получить, используя метод нахождения Z-преобразования.

т. к. Z-преобразование  то
то
получим передаточную функцию цифрового регулятора в виде:

Перейдем к разностному уравнению:




При решении задачи нахождение разностных уравнений регуляторов осуществить различными методами.
Уравнения непрерывных регуляторов и их передаточные функции:
1. ПИ-регулятор.

2. ПД-регулятор.
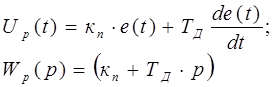
3. ПИД-регулятор.
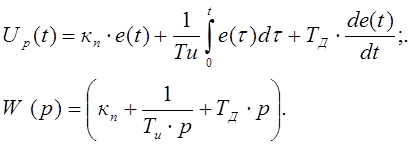
4. ПИ2-регулятор.

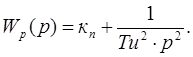
5. ПД2-регулятор.

6. ИА-регулятор.


При получении разностного уравнения следует учитывать соотношения для первой и второй разности (обратной).

Пример программы реализации И-регулятора представлен в [1].
Задача 4. Характеристический полином замкнутой цифровой системы регулирования скорости имеет вид:
1) 
Используя W-преобразование, проверить устойчива или нет данная система. Коэффициенты характеристического полинома заданы в таблице12.
Таблица 12
| Номер последней цифры шифра | d1 | d2 | d3 |
| 0 | -2,5 | 2,12 | -0,606 |
| 1 | -1,51 | 1,4 | 0,6 |
| 2 | +1,2 | -2,3 | -0,4 |
| 3 | +3,5 | +1,6 | +2,2 |
| 4 | 1,7 | -2,3 | +0,8 |
| 5 | -3,2 | +1,1 | -0,5 |
| 6 | -2,2 | 1,7 | -1,5 |
| 7 | +2,4 | -2,1 | +0,7 |
| 8 | -2,1 | +1,5 | -1,0 |
| 9 | +1,8 | +1,6 | -1,3 |
|
из
5.00
|
Обсуждение в статье: Методические указания к решению задачи 3 |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

