Методические указания к решению задачи 3

При круговой интерполяции следует использовать оценочную функцию вида:

F_i = x_i² + y_i² – R².

При отработке траектории в 1 квадранте против часовой стрелки, если применяется обычный алгоритм интерполяции, то расчетные соотношения примут вид:

· если F_i ≥ 0 (нахождение за пределом радиуса окружности), то шаг делается вдоль отрицательного направления оси х, т. е. х_i+1 = x_i – 1

F_i+1 =(x_i – 1)² +y_i² – R² = F_i – 2x_i + 1,

· если F_i < 0, то шаг делается в положительном направлении оси у, т. е. y_i+1 = y_i + 1

F_i+1 =x_i ² + (y_i +1)²  – R² = F_i + 2y_i + 1.

При применении усовершенствованного алгоритма рекомендуется разбить квадрант пополам (π/4). При изменении угла от φ = 0, до φ =π/4 и при F_i ≥ 0 выдача шагов осуществляется по обеим координатам:

F_i+1 =(x_i – 1)² +(y_i +1)²  – R² = F_i – 2(x_i – y_i) + 2,

а при F_i < 0 только по ведущей координате (у_i)

F_i+1 = F_i + 2y_i + 1.

При изменении угла от π/4 до π/2 и F_i < 0 выдача шагов производится по обеим координатам, а при F_i ≥ 0 только по ведущей координате (х_i)

F_i+1 = F_i – 2x_i + 1.

Следует отметить, что при усовершенствованном алгоритме интерполяции затрачивается меньшее число тактов, что приводит к увеличению контурной скорости отработки траектории.

Если перемещение должно осуществляться в других квадрантах в выбранном направлении (по часовой стрелке или против часовой стрелки), то аналогично рассмотренному выше можно получить необходимые расчетные соотношения для F_i+1.

Приведенный ниже алгоритм предназначен для реализации метода оценочной функции во всех 4 квадрантах при движении в любом направлении [5]:

Принятые обозначения: I, J – координаты центра дуги;

                                    r – радиус дуги;

                                    τ – такт;

                                    F – скорость подачи, мм/ мин;

                                   d = h – дискретность системы ЧПУ, мм;

                                    у_н, х_н – начальная точка;

                                    у_к, х_к – конечная точка.

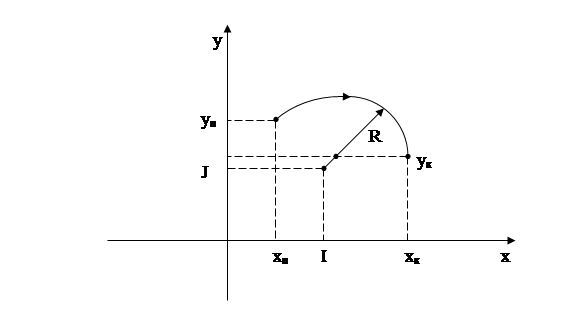
CIR: if TAKT > 1 then go to CYCLE

read x_н , у_н , х_к ,у_к , I, J, ±F

r = sqr((x_н – I)² + (у_н  - J)²)

x = x_н ; y = у_н ; codx = x; cody = y; f = 0

U= int(F*τ/(60*d));

if x_н = I and у_н > J then α_н = π/2

if x_н = I and у_н < J then α_н = 3*π/2

if x_н > I then α_н = atn((у_н – J)/( x_н – I))

if x_н < I then α_н = π + atn((у_н – J)/( x_н – I))

if x_к = I and у_к > J then α_к = π/2

if x_к = I and у_к < J then α_к = 3*π/2

if x_к > I then α_к = atn((у_к – J)/( x_к – I))

if x_к < I then α_к = π + atn((у_к – J)/( x_к – I))

if sgn(α_н - α_к) = sgn(U) then ∆α = abs(α_н - α_к)

else ∆α = 2π - abs(α_н - α_к)

L = 4 * r * ∆α/π ; l = 0

 

CYCLE: X = x – I; Y = y – J;

if abs(X) >= abs(Y) and sgn(f*sgn(X)*sgn(Y)) = sgn(U)

then(y = y – U*sgn(X); f = f – 2*Y*sgn(X) + U; go to END);

if abs(X) < abs(Y) and sgn(f*sgn(X)*sgn(Y) < > sgn(U)

then (X = X + U*sgn(Y); f = f + 2*X*sgn(Y) + U; go to END);

x = x + U*sgn(Y); y = y – U*sgn(X);

f = + 2*(abs(X) – abs(Y))*sgn(Y) + 2*U;

END: l = l + abs(X – codx) + abs(y – cody);

codx = x; cody = y;

if l < L then TAKT = TAKT + 1

else TAKT = 1

RETURN

 

Ниже приводится листинг программы на языке Си, которая реализует алгоритм оценочной функции, приведенный выше, с небольшими модификациями. Скорость подачи принята 1 шаг за один цикл алгоритма, направление движения по окружности зависит от введенных координат центра, начальной и конечной точек.

 

# include < stdio . h > /* Подключение библиотеки стандартных функций ввода-вывода */

# include < math . h >  /* Подключение библиотеки математических функций */

#define PI 3.1415         /* Определение числа p */

#define SGN(a) (((a) >= 0) ? 1 : -1) /* Определение макроса для вычисления знака переменной; макрос возвращает 1, если значение переменной ≥0 и возвращает -1, если значение переменной <0 */

int x _ n , y _ n , x _ k , y _ k , I , J ; /* Объявление целочисленных входных переменных для алгоритма: x _ n – начальная точка по оси X , y _ n – начальная точка по оси Y , x _ k – конечная точка по оси X , y _ k – конечная точка по оси Y , I – координата центра по оси X , J – координата центра по оси Y */

int x , y , r , codx , cody , f , L , l , X , Y ;  /* Объявление целочисленных внутренних переменных алгоритма: x , y – текущие координаты, r – радиус дуги, codx , cody – переменные для передачи координат исполнительному устройству, f – значение оценочной функции, L – полная длина пути по дуге, l – текущая пройденная длина, X , Y – разница между текущими координатами и центром окружности */

float a _ n , a _ k , da ; /* Объявление вещественных внутренних переменных алгоритма: a _ n – начальный угол в радианах, a _ k – конечный угол в радианах, da – отрабатываемый по дуге угол ( a _ k – a _ n ) */

/* Определение функции инициализации алгоритма */

void init() {

printf ("Введите x _ n , y _ n , x _ k , y _ k , I , J : "); /* Вывод сообщения с просьбой ввести значения входных переменных */

scanf ("% d % d % d % d % d % d ", & x _ n , & y _ n , & x _ k , & y _ k , & I , & J ); /* Ввод входных переменных пользователем */

r = sqrt((x_n - I)*(x_n - I) + (y_n - J) * ( y_n - J)); /* Вычисление радиуса дуги */

x = x_n;

y = y_n;

codx = x;

cody = y;

f = 0; /* Установка начальных значений внутренних переменных */

/* Вычисление начального угла по значениям x _ n , y _ n , I , J */

if(x_n == I && y_n > J)

    a_n = PI / 2;

if(x_n == I && y_n < J)

    a_n = 3 * PI / 2;

if(x_n > I)

    a_n = atan((y_n - J) / (x_n - I));

if(x_n < I)

    a_n = PI + atan((y_n - J) / (x_n - I));

/* Вычисление конечного угла по значениям x _ k , y _ k , I , J */

if(x_k == I && y_k > J)

    a_k = PI / 2;

if(x_k == I && y_k < J)

    a_k = 3 * PI / 2;

if(x_k > I)

    a_k = atan((y_k - J) / (x_k - I));

if(x_k < I)

    a_k = PI + atan((y_k - J) / (x_k - I));

da = a _ n - a _ k ; /* Вычисление угла поворота */

L = floor (4 * r * fabs ( da ) / PI + 0.5); /* Вычисление длины пути по дуге */

l = 0; /* Установка текущей длины пути в 0 */

printf("init: r=%d, a_n=%f, a_k=%f, da=%f, L=%d\n", r, a_n, a_k, da, L); /* Вывод на экран результатов инициализации */

}

/* Функция расчета очередного шага алгоритма оценочной функции */

void circle() {

/* Вычисление разницы между текущими координатами и центром окружности */

X = x – I ;

Y = y - J;

/* Вычисление нового значения оценочной функции и перемещение по соответствующим осям в зависимости от текущих координат и текущего значения оценочной функции */

if(abs(X) >= abs(Y) && SGN(f) * SGN(X) * SGN(Y) == SGN(da)) {

    y = y - SGN ( X ) * SGN ( da ); /* Изменение координаты y */

    f = f - 2 * Y * SGN ( X ) * SGN ( da ) + 1; /* Изменение значения оценочной функции */

}

else

if(abs(X) < abs(Y) && SGN(f) * SGN(X) * SGN(Y) != SGN(da)) {

    x = x + SGN ( Y ) * SGN ( da ); /* Изменение координаты x */

    f = f + 2 * X * SGN ( Y ) * SGN ( da ) + 1; /* Изменение значения оценочной функции */

}

else {

    x = x + SGN ( Y ) * SGN ( da ); /* Изменение координаты x */

    y = y - SGN ( X ) * SGN ( da ); /* Изменение координаты y */

/* Изменение значения оценочной функции */

    f = f +2 * ( abs ( X ) - abs ( Y )) * SGN ( Y ) * SGN ( X ) * SGN ( da )+ 2 * 1;

}

l = l + abs ( x - codx ) + abs ( y - cody ); /* Изменение пройденного пути */

codx = x ; cody = y ; /* Установка переменных для передачи исполнительному устройству */

printf (" f =% d \ tcodx =% d \ tcody =% d \ tl =% d \ n ", f , codx , cody , l ); /* Вывод результатов очередного шага алгоритма на экран */

}

/* Главная функция программы, с нее начинается выполнение */

int main () {

/* Вызов функции инициализации алгоритма оценочной функции */

init();

/* В этом месте можно передать начальные координаты cod _ x и cod _ y (равные x _ n и y _ n ) на исполнительное устройство */

/* Организация циклического вызова функции расчета очередного шага оценочной функции до тех пор пока текущий пройденный путь меньше полной длины пути по дуге */

while(l < L) {

    circle();

    /* В этом месте можно передать рассчитанные координаты cod _ x и cod _ y на исполнительное устройство */

}

return 0; /* Завершение главной функции программы */

}