Оценка технического состояния трансформаторных вводов на основе теории нечетких множеств

Традиционным методам диагностики трансформаторных вводов присущи многие недостатки, так как они не учитывают существующую неполноту и нечеткость информации о состоянии ввода.

Анализ опытов диагностики вводов обнаруживает, что для большинства случаев существует такое решающее правило "если параметр X не выше нормы Xн, то ..., а если параметр X выше нормы Xн , то ... ". Норма Xн обычно определяется из результата статистической обработки аварийных состояний по параметру X, однако чем больше мощность и класс напряжения силового трансформатора, тем скуднее такая статистика в связи с трудностью ее реализации. Это привело к тому, что норма Xн - нечеткая величина и нет резких границ или жестких граней, отделяющих одно состояние ввода от другого.

Другое непростое обстоятельство при диагностике вводов по традиционным методам заключается в том, что количество контролируемых параметров значительно, поэтому количество комбинаций этих параметров (при разных условиях) довольно большое. А опыт диагностики в виде решающих правил "если параметр X₁..., параметр X₂..., ..., параметр X_п..., то ..." не охватывает полный набор комбинаций параметров. Отсюда возникает вопрос: если комбинация параметров находится вне существующих решающих правил, то какое решение необходимо принимать в таком случае ?

Для преодоления этих трудностей целесообразно применять теорию нечетких множеств Заде [9]. Эта теория была предложена для количественного анализа таких гуманистических систем как лингвистика, экономика, политика. Однако в последнее время отмечено применение теории нечетких множеств в технике для решения задач проектирования и управления в медицинской диагностике.

В теории канторовских множеств произвольное подмножество А универсального множества U однозначно определяется своим индикатором:

 

 

Заде расширил класс подмножества U, введя понятие нечеткого, "расплывчатого" множества. Нечеткому множеству соответствует обобщенный индикатор (числовые функция со значениями из всего отрезка [0,1]), получивший название функции принадлежности µ(x). Тогда справедливо следующее определение: нечеткое множе-ство содержит элементы с функциями принадлежности, принимаю-щими любые значения на интервале [0,1], хотя бы одна из которых отлична от единицы.

Ниже приведем основные определения и операции с нечеткими множествами, которые необходимые нам при решении задачи диагностики трансформаторных вводов [8].

Объединением нечетких множеств А и В в пространстве X называется нечеткое множество А и В с функцией принадлежности, определяемой соотношением вида

 

,

 

или, в дизъюнктивной форме,

 

,

 

где символ ”V “ означает максимум.

Пересечением нечетких множеств А и В в пространстве V называется нечеткое множество А ^ В с функцией принадлежности, определяемой соотношением вида

 

,

 

или, в конъюнктивной форме,

 

,

 

где символ “ ^ ” означает минимум.

Согласно общего алгоритма [10] методика диагностики вводов на основе теории нечетких множества реализуется в несколько этапов.

На первом этапе необходимо определить возможный диапазон изменения контролируемых параметров состояния ввода и составить базу знаний на фоне решающих правил, которые были накоплены на практике диагностики вводов в течение многих лет, и отсюда вывести систему нечетких логических уравнений о диагнозах.

На втором этапе необходимо задавать вид функции принадлежности нечетких термов при разных контролируемых параметрах по мнениям опытного персонала по диагностике вводов.

На третьем этапе необходимо зафиксировать значения измеренных параметров состояния ввода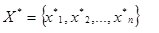

На четвертом этапе определяем функции принадлежности нечетких термов при фиксированных значениях измеренных параметров .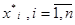

На пятом этапе вычисляем значения многопараметрических функций принадлежности при векторе состояния 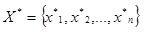для всех диагнозов d пользуясь логическими уравнениями из базы знаний. При этом логические операции И (^) и ИЛИ (V) над функциями принадлежности заменяются на операции min и max.

На шестом этапе определяем решение d, для которого

Этому решению и будет соответствовать искомый диагноз ввода с вектором параметров состояния

Аппаратная реализация этой методики реализуется с помощью элементов вычислительной техники. При этом вычислительная часть легко реализуется путем выполнения операций min и mах. Для изложения базы знаний будем обозначать: tgδ₁ - тангенс угла диэлектрических потерь основной изоляции (%); tgδ₃ - тангенс угла диэлектрических потерь наружных слоев изоляции (%); tgδ_м↓70C - тангенс угла диэлектрических потерь масла, измеренный при подъеме температуры в точке 70°С (%); tgδ_м↑70C -тангенс угла диэлектрических потерь масла, измеренный при снижении температуры в точке 70°С, после предварительной выдержки масла при температуре 90-100°С в течение 15-20 минут (%); Ai- значение концентрации растворенного в масле 1 -го газа или суммы концентраций газов (% об. 10^-4= мкл / л), где i - Н₂, С₂Н₂, ∑С_ХН_У = СН4 + С2Н2 + С2Н4 + С2H6; V_i - абсолютная скорость нарастания концентрации i-го газа или суммы газов (% об. 10^-4 / мес),

 

 

где А_iп- значение концентрации i -го газа при предыдущем измерении (все обозначения нижним индексом с буквой п означают предыдущее измерение), Т - промежуток времени с момента предыдущего измерения (мес.); V_∑- относительная скорость нарастания концентрации суммы всех газов (% / мес),

 

 

где А_iн- начальное (безопасное) значение концентрации i -го газа (% об. 10 ) определяется из табл. 7, N - граничное значение контролируемого параметра (Ai, tgδ, V, V_∑ и т.д.) определяется из табл.3.5-3.7.

На основании [11] приведем правила принятия решений, при этом мы постоянно будем обращаться к таблицам 3.2-3.6.

Правило 1: Вводы эксплуатируются с обычно принятой периодичностью контроля при выполнении следующих условий:

тангенс угла диэлектрических потерь основной изоляции tgδ₁ удовлетворяют условиям табл. 3.5;

-значение tgδ₁ возросло не более чем в 1.2 раза;

-тангенс угла диэлектрических потерь наружных слоев изоляции tgδ₃ не превышает значений, приведенных в табл. 3.5;

-значение tgδ₃ возросло не более чем в 1.5 раза по сравнению с предыдущими измерениями;

-значение tgδ₃ возросло не более чем в 2 раза по сравнению с данными при вводе в эксплуатацию;

-тангенс угла диэлектрических потерь масла на спаде температуры (tgδ_м↓70C) не превышает значений, приведенных в табл. 3.5 (если такие измерения проводились);

-концентрация содержания любого из газов Н₂, С2Н2, С_ХН_У не превышает значений, приведенных в табл.3.5, а соотношение А_CO/А_CO2<0.2;

-относительная скорость увеличения концентрации суммы горючих газов Н₂ + ∑С_ХН_У в месяц (V_∑).

V_∑< 10 (%/мес.) при периодичности контроля через 1 год,

V_∑< 4 (%/мес.) при периодичности контроля через 3 года.

Эти условия в наглядном виде приведены в таблице 3.2.

Правило 2: Вводы подлежат немедленной отбраковке при выполнении одного из следующих условий:

-имеется tgδ₃ > 1.5 N, по табл. 3.5;

-значение tgδ₁ увеличивалась более чем в 1.2 раза по сравнению с предыдущим измерением, а tgδ₃ превышает значения, приведенные в табл. 3.5;

- концентрация растворенных газов превышает значения по табл. 3.8, а тангенс наружных слоев изоляции tgδ₃ превышает значения,приведенные в табл. 3.5;

- концентрация газов Н₂, С₂Н₂ и ∑С_ХН_У превышают или равны значениям, приведенным в табл. 3.5 одновременно;

-абсолютная скорость нарастания любого из газов Н₂, С₂Н₂, и ∑С_ХН_У превышает значения, приведенные в табл. 3.6;

- тангенс угла диэлектрических потерь масла, измеренный при подъеме и на спаде температуры превышают значения, приведенные в табл. 3.7 и 3.5 соответственно (если проводился отбор пробы масла);

- концентрация любого из газов Н₂, С₂Н₂ и ∑С_ХН_У превышает в 2 и более раза значения, приведенные в табл. 3.5;

- величина tgδ₃ превышает значения, приведенные в табл. 3.5 и значения tgδ_3п при предыдущем измерении, при этом относительная скорость нарастания суммы горючих газов в месяц V_г превышает значений по табл. 3.2.

Эти условия в наглядном виде приведены в таблице 3.3. Отмечаем особый случай, когда tgδ₁<0. При этом если tg₁ превышает значения, приведенные в табл.4 то считают, что ввод подлежит отбраковке, а если tgδ₃ меньше нормы по табл. 3.5 то необходимо убедиться в истинности результатов измерений. Для этого необходимо предпринять меры по исключению влияния погодных условий и загрязнения внешней изоляции.

Правило 3: Вводы с предполагаемым наличием дефекта, у которых значение контролируемых параметров отклоняются от нормы, требуют уточнения диагноза эксплуатационного состояния. Для этого необходимо увеличить объем испытаний, провести дополнительные измерения или повторный контроль при сокращенной периодичности. Правило формируется в виде "если ... то ...".

-если значение tgδ₁ лежит в пределах величин, приведенных в табл. 3.5, а tgδ₃ превышает указанное в табл. 3.5, но не более чем в 1.5 раза, а концентрации газов не превышают значений табл. 3.8, то необходимо произвести отбор пробы масла для измерения tgδ_м↑70C и tgδ_м↓70C измеренные при подъеме и спаде температуры, если эти тангенсы не превышают значений в табл. 3.7 и 3.5 соответственно, то допустима проведение повторного контроля через год;

- если значение tgδ₁ лежит в пределах величин, приведенных в табл. 3.5, а tgδ₃ превышает указанное в табл. 3.5, но не более чем в 1.5 раза, а концентрация газов превышает значения по табл. 3.8, но не более граничных значений по табл. 3.5, а относительная скорость нарастания суммы горючих газов в месяц V₁ < N (табл. 3.2) то допустимо проведение повторного контроля через 0.5 года;

- если концентрации растворенных газов достигают граничных значений только за счет содержания Н₂ и СH₄, но не более удвоенного значения по табл. 3.5 и при этом А_CO/А_CO2 < 0.15, то допустимо проведение повторного контроля через 0.5 года;

-если установлено, что относительная скорость нарастания суммы горючих газов в месяц V_∑ не превышает значений по таб. 3.2, а концентрация каждого из газов Н₂, С₂Н₂ и ∑С_ХН_У не превышает значений по табл. 3.5, или концентрация газов превышает граничное значение, но не более удвоенного граничного значения по табл. 3.5 только по отдельным газам, то необходимо произвести повторный контроль не позднее, чем через время

 

 

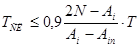
где N - граничные значения концентраций газов по табл. 3.5; А_{i ,}А_iП - концентрации газов, полученные при последнем и предыдущем измерении соответственно; Т - период между последним и предыдущим измерением; Т_сл - минимальное значение из рассчитанных по газам Н₂, ∑С_ХH_У по выражению в правой части выше приведенного неравенства.

Эти условия в наглядном виде приведены в таблице 3.4.

 

 

 

 

 

 

 

В соответствии с базой знаний (табл.3.2-3.4) будем определять следующие технические состояния:

 

Таблица 3.9

dm	Рекомендации по дальнейшей эксплуатации
d1	ввод нормально эксплуатируется с обычно принятой периодичностью контроля
d2	ввод подлежит немедленной отбраковке
d3	ввод с предполагаемым наличием дефекта, требует уточнения диагноза эксплуатационного состояния, допустимо оставить в эксплуатации с периодичностью контроля не позднее 1 год
d4	ввод с предполагаемым наличием дефекта, требует уточнения диагноза эксплуатационного состояния, ввод допустимо оставить в эксплуатации с периодичностью контроля не позднее 0,5 года
d5	ввод с предполагаемым наличием дефекта, требует уточнения диагноза эксплуатационного состояния, ввод допустимо оставить в эксплуатации с расчетной периодичностью контроля

 

Исходя из базы знаний, целесообразно ввести следующие входные параметры с соответствующими возможными диапазонами изменения [11]:

 

Таблица 3.10

 

В случае, когда при измерении x₁ <0, то необходимо проверить тщательно результаты других измерений и повторно производить измерение параметра x₁. Если это подтверждается, то ввод подлежит отбраковке.

Задача диагностики состоит в том, чтобы каждому сочетанию значений факторов поставить в соответствие одно из решений d_m.

Параметры x₁-x₁₈, определенные выше, будем рассматривать как лингвистические переменные. Кроме того, введем еще одну лингвистическую переменную: d - опасность повреждения ввода, которая измеряется уровнями d₁ - d₅.

Для оценки значений лингвистических переменных x₁, x₂, x₅, x₆, x₁₇, x₁₁, x₁₂, x₁₃, x₁₄, x₁₅, x₁₆, x₁₇ будем использовать два терма: Н - низкий, В – высокий. Для оценки значений лингвистических переменных x₃, x₄, x₈, x₉, x₁₀, x₁₈ будем использовать три терма: Н - низкий, С - средний, В – высокий. Каждый из этих термов задает нечеткое ограничение на множество, заданное с помощью соответствующей функции принадлежности.

Предполагаем, что функции принадлежности параметров x_1,, x₂, x₅, x₆, x₁₇, x₁₁, x₁₂, x₁₃, x₁₄, x₁₅, x₁₆, x₁₇ имеют одинаковый вид для каждого терма Н или В.(рис. 3.7.); функции принадлежности параметров x₃, x₄, x₈, x₉, x₁₀, x₁₈ имеют одинаковый вид для каждого терма Н, С или В (рис. .8.).

 

 

 

 

Из таблиц 3.2 – 3.4 формулируем следующие нечеткие высказывания:

1)ЕСЛИ (x₁= Н) и (x₂ = Н) и (x₁- Н) и [(x₁= Н) или (x₄ = С)] и

(x₅ = Н) и (x₇ = Н) и (x₈ = Н) и (x₉ = Н) и (x₁₀ = И) и (x₁₁=Н) и [(x₁₈= Н) или (x₁₈ = С)],

то d = d₁

2)ЕСЛИ [x₃ = В),

или [(x₃ = С) и (x₂ = В)],

или {( x₃ = С) и [(x₁= В) или (x₁₃ = В) или (x₁₄=B)]}_э

или [(x₈ = С) и (x₉ = С) и (x₁₀ = С)],

или (x₁₅ = В),

или (x₁₆ = В),

или (x₁₇ = В),

или [(x₆ = В) и (x₇ = В)],

или (x₈ = В),

или (x₉ = В),

или (x₁₁ = В),

или {(x₃ = С) и [(x₄ = С) или (x₄ = В)] и (x₁₁ =В)},

то d = d₂

3)ЕСЛИ [(x₃=С) и (x₁= Н) и (x₁₂ = Н) и (x₁₃ = Н) и (x₁₄ = Н) и(x₆ = Н) и (x₇ = Н)],

то d = d₃

4)ЕСЛИ [(x₃ = С) и (x₁ = Н) и (x₁₂ = В) и (x₁₃ = В) и (x₁₄ = В) и(x₈ = Н) и (x₉ = Н) и (x₁₀ = Н) и (x₁₁ = Н)] или [(x₁₈ = Н) и (x₈=С) и (x₁₀ = С) и (x₁₃ = Н)],

то d = d₄

5)ЕСЛИ [(x₁₁ = В) и (x₈ = Н) и (x₉ = Н) и (x₁₀ - Н)], или {( x₁₁ =В) и [(x₈ = С) или (x₉ = С) или (x₁₀=С)]},

то d = d₅

Пользуясь функциями принадлежности, запишем эти логические высказывания в виде логических уравнений. При этом заменяем слово "и" операцией “^” (для краткости будем использовать знак "•", слово "или" операцией “V”.

 

 

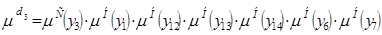
Согласно общего алгоритма [10], решению задачи диагностики соответствует тот диагноз, который имеет максимальное значение функции принадлежности:

 

 

Однако для нашей задачи диагностики, в некоторых случаях нет необходимости вычислять все одномерные и многомерные функции принадлежности.

Отметим, что из выше приведенных правил ЕСЛИ...ТО... можно получить однопарамстрические правила:

ЕСЛИ (x₃=В), то d = d₂;

ЕСЛИ (x₈ = В), то d = d₂;

ЕСЛИ (x₉ = В), то d = d₂;

ЕСЛИ (x₁₀ = В), то d = d₂;

ЕСЛИ (x₁₅=В), то d = d₂;

ЕСЛИ (x₁₆ = В), то d = d₂;

ЕСЛИ (x₁₇ = В), то d = d₂;

(при этом необходимо учитывать, что параметр xз измеряется по мостовой схеме, а параметры x₈, x₉, x₁₀, x₁₅, x₁₆, x₁₇ измеряются по методу хроматографического анализа);

двухпараметрические правила:

ЕСЛИ [(x₃=С) и (x₂ = В)], то d = d₂;

ЕСЛИ [(x₆ =В) и (x₇= В)], то d = d₂;

трехпараметрические правила:

ЕСЛИ [(x₈ = С) и (x₉ = С) и (x₁₀ = С)], то d = d₂;

ЕСЛИ {(xз = С) и [(x₄=С) или (x₄ = В)] и (x₁₁ = В)}, то d = d₂;

четырехпараметрические правила:

ЕСЛИ {(x₃ =С) и [(x₁₂=В) или (x₁₃ = В) или (x₁₄ = В)]},

то d = d₂

ЕСЛИ [(x₁₈ = Н) и (x₈ = С) и (x₁₀ = С) и (x₁₃ = Н)]

то d = d₄ ;

ЕСЛИ [(x₁₁ = В) и (x₈ = Н) и (x₉ = Н) и (x₁₀ = Н)],

то d = d₅;

ЕСЛИ {( x₁₁=В) и [(x₈=С) или (x₉ = С) или (x₁₀ = С)]},

то d = d_5;

семипараметрическое правило:

ЕСЛИ [(x₃ = С) и (x₁ = Н) и (x₁₂ = Н) и (x₁₃ = Н) и (x₁₄ = Н) и

(x₆ = Н) и (x₇ = Н)], то d = d₃;

девятипараметрическое правило: ЕСЛИ [(x₃=С) и (x₁= Н) и (x₁₂ =В) и (x₁₃= В) и (x₁₄ = В) и (x₈ = Н) и (x₉ = Н) и (x₀ = Н) и (x₁₁ = Н)],

то d = d₄

одиннадцатипараметрическое правило:

ЕСЛИ (x₁ = Н) и (x₂ = Н) и (x₃ = Н) и [(x₄ = Н) или (x₄ = С)] и (x₅ = Н) и (x₇= Н) и (x₈ = Н) и (x₉ = Н) и (x₁₀ = Н) и (x₁₁ = Н) и [(x₁₈ = Н) или

(x₁₈ = С)],

то d = d₁;

Отсюда следует целесообразность контроля в первую очередь по однопараметрическим правилам сначала параметра x₃. Если x₃ = В (при этом будем условно говорить, что параметр x₃ больше принадлежит терму В, то сразу принимаем решение d = d₂, иначе проверяем один из параметров x₈ , x₉ , x₁₀, x₁₅, x₁₆, x_17. Если один из этих параметров больше принадлежит терму В, то также сразу принимаем решение d₂, иначе проверяем по двухпараметрическим правилам путем дополнительного рассмотрения параметра x₂ (учитываем, что параметр x₂ измеряется одновременно с параметром x₃ при контроле на подстанции по методу измерения tg). Если условия по двухпараметрическим правилам не выполняются, то переходим к трехпараметрическим правилам и т.д.

Если измеряемые параметры не выполняются ни в одном из правил в базе знаний, то в этом случае необходимо вычислить многопараметрические функции принадлежности, исходя из однопараметрических функций принадлежности по формулам, а затем принимать решение.

Традиционная диагностика по правилам 1, 2, 3 является частным случаем предложенной выше методики с применением теории нечетких множеств.

Таким образом, целесообразно совмещать правила традиционной диагностики и теорию нечетких множеств, поскольку операции сравнения легче выполнять, чем вычисления функции принадлежности. В случае, когда правила традиционной диагностики не срабатывают, следует вычислять функции принадлежности.

Ниже приведем один практический пример, при котором правила традиционной диагностики не позволяют принять решение, а основанные на теории нечетких множеств - позволяют.

Данные измерений для диагностики ввода 110 кВ с маслом типа ГК приведены в таблицах 3.11 и 3.12.

Подставляя данные из таблиц 3.11 и 3.12 в формулы для x с учетом таблиц 3.5 – 3.8, получим значения параметров x. Проверка по одно-, двух-, трех-, четырех-, семи-, девяти- и одиннадцатипараметрическому правилу не дает ответа на диагноз. Это значит, что традиционная диагностика неприемлема в этой ситуации.

Подставляя в формулы найденные значения x, получим значения функций принадлежности. Все эти величины приведены в таблице 3.13.

Поставляя значения функций принадлежности из таблицы 3.13 получим:

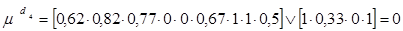
Отсюда следует, что среди пяти диагнозов максимальное значение функции принадлежности имеет диагноз d₂. Следовательно, ввод подлежит немедленной отбраковке.

 

Таблица 3.11 Данные измерений  (%)

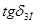
1,06	1,0	1,4	1,0	0,8	1,2	1,3

 

Таблица 3.12 Данные измерений по методу ХАРГ (% об. )

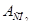
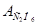
240	0	410	3	4	0	1	8
110	0	123	2	2	0	0	4

 

 

Список литературы

 

1. Рыжкин В.Я. Тепловые электрические станции. - М.: Энергия, 1992.-276с.

2. Тепловые и атомные станции. Книга 3. Справочник. Под ред. В.А. Григорьева, В.М. Зорина. 2-е издание, переработанное –М.: «Энергия», 1989, - 600 с.

3. Рыжкова Л.Д., Козулин В.С. Электрооборудование станций и подстанций. Учебник для техникумов. – 2-е изд., перераб. - М.: «Энергия», 1980, - 600 с.

4. Электрическая часть электрических станций и подстанций. Под ред. А.А. Васильева. Учебник для вузов - М., «Энергия», 1980. - 608 с.

5. Электрическая часть электрических станций и подстанций. Справочные материалы для курсового и дипломного проектирования. Под ред. Б.Н. Неклепаева. Изд.2 -е , перер. М., «Энергия», 1972. - 336 с.

6. Околович М. Н. Проектирование электрических станций: Учебник для вузов. - М.: Энергоатомиздат, 1982. - 400 с.

7. Бажанов С.А., Воскресенский В.Ф. Монтаж и эксплуатация маслонаполненных вводов.-М.:Энергоатомиздат, 1981.-104с.

8. Штовба С.Д. Введение в теорию нечетких множеств и нечеткую логику.

9. Заде Л.А. Понятие лингвистической переменной и ее применение к принятию приблеженных решений. М., 1976.

10. Ронштейн А.П. Медицинская диагнстика на нечеткой логике. – Винница: Континент – ПРИМ, 1996. – 132с.

11. Галузевий керівний документ. Маслонаповнені вводи напругою 110 – 750 кВ. Типова інструкція з експлуатації. – Київ, 2004

12. Методические указания по диагностике состояния изоляции высоковольтных вводов 110 – 750 кВ. М.,1990.

13. Методичні вказівки з техніко – економічного обгрунтування інвестиційних проектів електричних станцій. Уклад.: Є.Г. Скловська, К.Г. Тодорович. – К.: Політехніка, 2002. – 24с.

14. Охрана труда в єлектроустановках: Учебник для вузов / Под ред. Б.А. Князевского. – 3-е изд., перераб. И доп. – М.: Єнергоатомиздат, 1983. – 336 с.