Предлагаемый метод заключается в следуюшем

     - задайте показатель степени n

     - используя бином Ньютона, раскройте выражение ( b + c + d ) ⁿ

   - попробуйте получить равенство A ( b , с, d ) = ( c + d ) ⁿ , где A ( b , с, d )- остаток от бинома Ньютона, т.к. ( b + c + d ) ⁿ = ( b + c ) ⁿ + A ( b , с, d ). Это возможно только для n = 2.

2.                  Формулы (9), (10), (11)

                        X = n² + 2mn

                                  Y = 2m² + 2mn

                                  Z = n² + 2mn + 2m² .

У читателя может возникнуть вопрос – “ Что дает переход к этим формулам в сравнении с известными X = 2 pq , Y = p ² – q ² , Z = p ² + q ² ? “.

                      2.1 Степенные функции

 1. Рассмотрим уравнение aX ² + bX + с = 0. Пусть X = n ² + 2 mn

→          a(n² + 2mn )² + b(n² + 2mn ) + с =0

→ an⁴ + 2an²(2mn) + a(2mn)² + bn² + b(2mn) + с = 0

→ (an⁴ + bn² + с ) + [4an²(2mn) + a(2mn)² + b(2mn)] = 0    

Обратим внимание на то, что здесь первое слагаемое имеет вид исходной функции, если считать, что x=n² .

Допустим, что x=n² тогда из уравнения ( ) получим

                         2an²(2mn) + a(2mn)² + b(2mn) = 0           (14)          

откуда (2mn)₁=0 , т.е. мы подтвердили принятое ранее допущение 

                                         x=n²+2mn при (2mn)₁=0 ® x=n²

Из (14) имеем

                               2an²+ a(2mn) + b= 0

    →                        mn =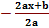   

    →                               X =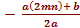                                                                                                 

Обратим внимание на то, что y'=(2ax+b), y''=2a       

      где y' - первая производная по x от исходной функции,         

            y''- соответственно 2-ая производная.

Подставим это значение x в исходное уравнение (1) и приравняем нулю

              → a[ 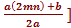² – b[  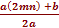] + с = 0  

              →    (2mn)² =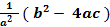     

Если квадратное уравнение решить обычным способом, то получим

                        ( X₁ – X₂ )² =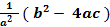

                →    (2mn)² = ( X₁ – X₂ )²

     где x₁, x₂-корни исходного уравнения.

На основании результатов проведенного расчета можно сделать следующее утверждение

Утверждение 1. Для квадратного уравнения вида aX² + bX + с = 0 справедливо равенство

                               (2mn)² = ( X₁ – X₂ )² = (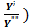

где

              - (2mn) - параметр системы,    

              -x₁, x₂ - корни уравнения ,          

              -y', y"- производные по x.

Рассмотрим функцию aX³ + bX² + сX + d = 0. Пусть X = n²+2mn 

   → a(n² + 2mn )³ + b(n² + 2mn )² + с (n² + 2mn ) + d =0

Откуда, аналогично расчетам п.1,получим

       a( 2mn )³ + (3ax + b)(2mn )² + 3ax² + 2bx + с = 0  (16)

Легко проверить, что вместо этого уравнения можно записать

                ² +

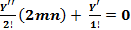
Для функции aX⁴ + bX³ + сX² + dX + e = 0  аналогично получим 

                 ³ +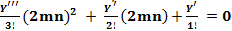  

На основании формулы (16) автором разработан новый метод решения

любого кубического уравнения включая неприводимый случай формулы Кардана(см.сайт fgg-fil1.narod.ru ).

Из анализа полученных формул следует

Утверждение 2. Для функции вида y = ax^k + bx^k-1+…+ N = 0

справедливо уравнение

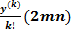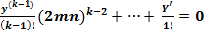        ^k-1 +              (17)

  где - y ^{( k )} к-ая производная исходной функции,

- y^(k-1) -ая производная,

- y ^(k-i) -ая производная,

- (2 mn ) -параметр системы m , n .

Следует сказать, что эта формула обладая внешним сходством с известной формулой Тейлора (см. любой справочник по математике), имеет в сравнении с ней следующие существенные отличия:

1.В формуле Тейлора имеет место 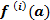, где а - конкретное значение переменной, т.е.

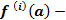     конкретное число, не содержащее переменной x.

В формуле 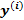может содержать переменную x.  

2.В ряде Тейлора имеет место при слагаемых множитель вида(x – a)^’   содержит только одну переменную  x . В формуле имеют место две переменные.  

3.В частном случае параметр (2mn)² = ( X₁ – X₂ )² , где xi, xi+1 -любая пара корней исходного уравнения. При этом число (2mn)_i²   равно числу сочетаний из n элементов (n -число корней исходного уравнения) по m .

                                                   C_n^m = .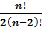

  3. Таблица вариантов значений параметров mn

Задача 3 В результате одиночного эксперимента получены координаты

одной точки M ( X , Y ). Для планирования последующих экспериментов необходимо знать дисперсию возможных координат точек ожидаемой функции. На основании данных одной точки M ( X , Y ) необходимо определить