 |
Главная |
Отношения эквивалентности на числовой прямой
|
из
5.00
|
Пусть задано отношение 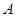 на множестве
на множестве 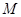 . В случае, когда
. В случае, когда 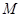 – числовая прямая, отношение
– числовая прямая, отношение 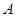 отождествляется с некоторым подмножеством числовой плоскости, т.е. прямого произведения
отождествляется с некоторым подмножеством числовой плоскости, т.е. прямого произведения 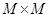 . В этом параграфе будут рассмотрены геометрические свойства множества
. В этом параграфе будут рассмотрены геометрические свойства множества 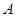 на плоскости в случае, когда отношение
на плоскости в случае, когда отношение 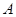 есть эквивалентность.
есть эквивалентность.
Согласно определению 1.2.1 отношение 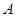 называется эквивалентностью, если оно рефлексивно, симметрично и транзитивно. Каждое из этих свойств порождает некоторое геометрическое свойство множества
называется эквивалентностью, если оно рефлексивно, симметрично и транзитивно. Каждое из этих свойств порождает некоторое геометрическое свойство множества 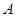 . Координаты точки на плоскости будем обозначать
. Координаты точки на плоскости будем обозначать 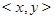 .
.
1. Рефлексивность. Из того, что 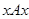 для всех
для всех 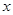 , следует, что множество
, следует, что множество 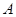 содержит главную диагональ (свойство
содержит главную диагональ (свойство  ).
).
2. Симметричность. Симметричность означает, что если 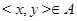 , то и
, то и 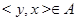 , т.е. что множество
, т.е. что множество 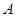 симметрично относительно главной диагонали (свойство
симметрично относительно главной диагонали (свойство 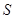 ).
).
3. Транзитивность. Транзитивность означает, что если  и
и 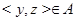 , то и
, то и 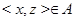 . Точка
. Точка 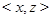 является четвертой вершиной прямоугольника, три вершины которого находятся в точках
является четвертой вершиной прямоугольника, три вершины которого находятся в точках 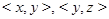 и
и 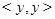 . Заметим, что вершина
. Заметим, что вершина 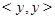 лежит на биссектрисе координатного угла – главной диагонали координатной плоскости. Поэтому геометрически свойство транзитивности можно сформулировать следующим образом:
лежит на биссектрисе координатного угла – главной диагонали координатной плоскости. Поэтому геометрически свойство транзитивности можно сформулировать следующим образом:
Множество 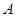 на плоскости определяет транзитивное отношение тогда и только тогда, когда для любого прямоугольника, одна вершина которого
на плоскости определяет транзитивное отношение тогда и только тогда, когда для любого прямоугольника, одна вершина которого 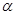 лежит на главной диагонали, а две соседние с
лежит на главной диагонали, а две соседние с 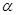 вершины принадлежат
вершины принадлежат 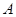 , вершина
, вершина 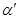 , противоположная
, противоположная 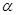 , также принадлежит
, также принадлежит 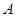 (свойство
(свойство 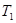 ).
).
Замечание. Если отношение 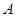 является симметричным, то геометрическая формулировка транзитивности несколько упрощается. А именно:
является симметричным, то геометрическая формулировка транзитивности несколько упрощается. А именно:
Множество 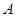 на плоскости, симметричное относительно главной диагонали, определяет транзитивное отношение тогда и только тогда, когда для любого прямоугольника, одна вершина которого лежит на главной диагонали, а две другие принадлежат
на плоскости, симметричное относительно главной диагонали, определяет транзитивное отношение тогда и только тогда, когда для любого прямоугольника, одна вершина которого лежит на главной диагонали, а две другие принадлежат 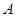 , четвертая вершина также принадлежит
, четвертая вершина также принадлежит 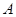 (свойство
(свойство 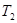 ).
).
Разница с предыдущим утверждением состоит в том, что вершины, принадлежащие 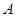 , не обязаны быть соседними с вершиной, лежащей на диагонали. Покажем, что для симметричного
, не обязаны быть соседними с вершиной, лежащей на диагонали. Покажем, что для симметричного 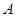 свойство
свойство  , влечет
, влечет 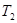 . Пусть, например, вершина, лежащая на диагонали, имеет координаты
. Пусть, например, вершина, лежащая на диагонали, имеет координаты 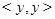 и
и 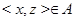 и
и 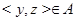 ; покажем, что
; покажем, что 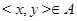 . В самом деле, в силу симметрии, вместе с
. В самом деле, в силу симметрии, вместе с 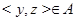 имеем
имеем 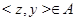 . Если в качестве вершины на диагонали взять теперь
. Если в качестве вершины на диагонали взять теперь 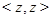 , а в качестве соседних с ней вершин, принадлежащих
, а в качестве соседних с ней вершин, принадлежащих 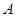 ,
, 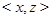 и
и 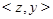 , то, в силу свойства
, то, в силу свойства 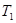 получаем
получаем 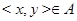 .
.
Заметим, что класс эквивалентности, содержащий точку 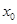 , есть проекция пересечения множества
, есть проекция пересечения множества 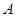 и прямой
и прямой 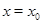 на ось ординат.
на ось ординат.
Сейчас мы приведем некоторые примеры множеств на плоскости, определяющих отношение эквивалентности.
1 Пример. (тривиальный). Множество 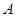 вся плоскость. Выполнение свойств
вся плоскость. Выполнение свойств 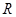 ,
, 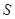 ,
, 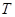 очевидно. Все точки исходной прямой
очевидно. Все точки исходной прямой 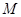 отождествляются, т.е. входят в один класс эквивалентности.
отождествляются, т.е. входят в один класс эквивалентности.
Замечание. Для любого 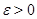 , если множество
, если множество 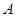 , определяющее отношение эквивалентности, содержит полосу
, определяющее отношение эквивалентности, содержит полосу 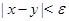 , то оно совпадает со всей плоскостью. В самом деле, вместе с любой точкой
, то оно совпадает со всей плоскостью. В самом деле, вместе с любой точкой  множество
множество 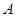 содержит все внутренние точки квадрата с вершинами
содержит все внутренние точки квадрата с вершинами 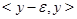 ,
, 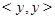 ,
, 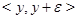 ,
, 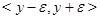 , т.е. полосу
, т.е. полосу 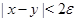 . Ясно, что таким образом свойство "принадлежать
. Ясно, что таким образом свойство "принадлежать 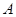 " распространяется на все точки плоскости.
" распространяется на все точки плоскости.
2 Пример. (периодичность). Возьмем которое число. Пусть множество 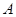 состоит из прямых
состоит из прямых 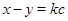 , где
, где 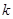 – произвольное целое число. Выполнение свойств
– произвольное целое число. Выполнение свойств  и
и 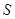 очевидно, и если
очевидно, и если 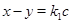 ,
, 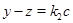 , то
, то 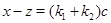 .
.
3 Пример. "Все константы равны единице, кроме нуля". (Такое утверждение высказал И.М. Гельфанд на одной из своих лекций.) В этом примере множество 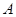 есть вся плоскость с выброшенными осями координат и добавленным началом координат. Иначе говоря,
есть вся плоскость с выброшенными осями координат и добавленным началом координат. Иначе говоря, 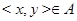 всегда, кроме случая
всегда, кроме случая 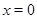 ,
, 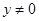 и ему симметричного. Если точки
и ему симметричного. Если точки 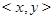 ,
, 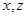 принадлежат
принадлежат 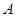 , то либо
, то либо 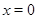 , и тогда
, и тогда 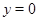 ,
, 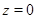 , либо
, либо 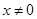 , и тогда
, и тогда 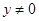 и
и 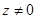 . В обоих случаях
. В обоих случаях 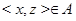 .
.
4 Пример. (Все целые числа равны друг другу.) Множество 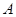 состоит из главной диагонали и всех точек с целыми координатами.
состоит из главной диагонали и всех точек с целыми координатами.
Очевидно, можно рассматривать и конечные варианты такой эквивалентности типа 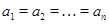
5 Пример. (Все числа, не большие единицы по модулю, равны друг другу.) Множество 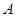 состоит из диагонали и замкнутого единичного квадрата. Очевидно, множество, состоящее из открытого (или полузамкнутого:
состоит из диагонали и замкнутого единичного квадрата. Очевидно, множество, состоящее из открытого (или полузамкнутого: 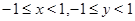 ) квадрата, также дает эквивалентность.
) квадрата, также дает эквивалентность.
|
из
5.00
|
Обсуждение в статье: Отношения эквивалентности на числовой прямой |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

