 |
Главная |
Формальные свойства эквивалентности
|
из
5.00
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
"Гомельский государственный университет имени Франциска Скорины"
математический факультет
Кафедра алгебры и геометрии
Курсовая работа
"Отношения эквивалентности и толерантности и их свойства"
Гомель 2005
Введение
В обыденной речи мы часто говорим об одинаковости (о равенстве) каких-то объектов (предметов, множеств, абстрактных категорий), не заботясь о надлежащем уточнении смысла, который мы вкладываем в слово "одинаковый". В главе первой попробуем выявить и раскрыть понятие "одинаковости", определим термины "эквивалентность" и "отношение эквивалентности".
Не менее важной является ситуация, когда нам приходится устанавливать сходство объектов. Если одинаковость объектов означает их взаимозаменимость в некоторой ситуации, то сходство – это частичная взаимозаменимость, т.е. возможность взаимной замены с некоторыми (допустимыми в данной ситуации) потерями, с допустимым риском. Во второй главе попробуем раскрыть понятие "толерантности" на базе таких терминов, как "одинаковость" и "сходство" объектов.
А в третьей главе подробнее рассмотрим применение понятий отношений эквивалентности и толерантности в различных областях знаний и практики человека.
Реферат

Курсовая работа содержит: 41 страница, 3 источника, 1 приложение.
Ключевые слова: отношение эквивалентности, отношение толерантности, одинаковость, сходство, взаимозаменимость, классы эквивалентности, пространство толерантности, классы толерантности, предкласс, базис.
Объект исследования: отношения эквивалентности и толерантности.
Предмет исследования: свойства отношений эквивалентности и толерантности.
Цель работы: используя рекомендуемую литературу рассмотреть понятия отношений эквивалентности и толерантности; рассмотреть приложения этих понятий в различных областях знаний и практики человека.
Методы исследования: методы теории множеств и теории отношений.
Задачами курсовой работы являются: изучить свойства отношений эквивалентности и толерантности и их приложения в конкретных областях знаний.
Отношение эквивалентности
Определение и примеры
Определение
Систему непустых подмножеств 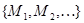 множества
множества 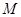 мы будем называть разбиением этого множества, если
мы будем называть разбиением этого множества, если
1) 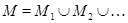 и
и
2) 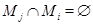 при
при 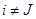 .
.
Сами множества 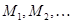 называются при этом классами данного разбиения.
называются при этом классами данного разбиения.
Определение
Отношение 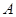 на множестве
на множестве 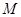 называется эквивалентностью (или отношением эквивалентности), если существует разбиение
называется эквивалентностью (или отношением эквивалентности), если существует разбиение 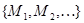 множества
множества 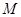 такое, что соотношение
такое, что соотношение 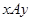 выполняется тогда и только тогда, когда
выполняется тогда и только тогда, когда 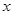 и
и 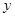 принадлежат некоторому общему классу
принадлежат некоторому общему классу 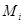 данного разбиения.
данного разбиения.
Пусть 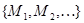 – разбиение множества
– разбиение множества 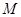 . Определим, исходя из этого разбиения, отношение
. Определим, исходя из этого разбиения, отношение 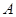 на
на 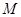 :
: 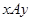 , если
, если 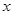 и
и 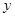 принадлежат некоторому общему классу
принадлежат некоторому общему классу 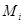 данного разбиения. Очевидно, отношение
данного разбиения. Очевидно, отношение 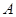 является эквивалентностью. Назовем
является эквивалентностью. Назовем 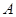 отношением эквивалентности, соответствующим исходному разбиению.
отношением эквивалентности, соответствующим исходному разбиению.
Например, разбиение состоит из подмножеств множества 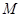 , содержащих ровно по одному элементу. Соответствующее отношение эквивалентности есть отношение равенства
, содержащих ровно по одному элементу. Соответствующее отношение эквивалентности есть отношение равенства 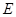 . Наконец, если разбиение множества
. Наконец, если разбиение множества 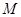 состоит из одного подмножества, совпадающего с самим
состоит из одного подмножества, совпадающего с самим 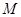 , то соответствующее отношение эквивалентности есть полное отношение: любые два элемента являются эквивалентными.
, то соответствующее отношение эквивалентности есть полное отношение: любые два элемента являются эквивалентными.
Пустое отношение (на непустом множестве!) не является эквивалентностью.
Мы подошли к эквивалентности через понятие взаимозаменимости. Но что значит, что два объекта 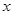 и
и 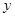 взанмозамепимы в данной ситуации? Это всегда можно понимать так, что каждый из них содержит всю информацию о другом объекте, небезразличную в данной ситуации. Это утверждение означает только то, что взаимозаменимость объектов есть совпадение признаков, существенных в данной ситуации.
взанмозамепимы в данной ситуации? Это всегда можно понимать так, что каждый из них содержит всю информацию о другом объекте, небезразличную в данной ситуации. Это утверждение означает только то, что взаимозаменимость объектов есть совпадение признаков, существенных в данной ситуации.
Например, пусть мы считаем одинаковыми автомобили, выпущенные в одной и той же серии одним и тем же заводом. Тогда, разобрав один экземпляр "Волги", мы в принципе можем составить комплект рабочих чертежей, который годится для выпуска однотипных "Волг". Однако, изучив один экземпляр "Волги", мы не можем угадать окраску кузова или характер вмятин на бампере у других односерийных экземпляров.
Когда мы выбираем из комплекта одну шахматную фигуру, то мы знаем, куда ее можно поставить в начальной позиции и как ходят, все взаимозаменяемые с ней, т.е. одноименные и одноцветные, фигуры.
Пусть теперь задано разбиение 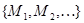 множества
множества 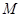 . Выберем в каждом множестве
. Выберем в каждом множестве 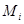 некоторый содержащийся в нем элемент
некоторый содержащийся в нем элемент 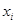 . Этот элемент мы будем называть эталоном для всякого элемента
. Этот элемент мы будем называть эталоном для всякого элемента 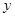 , входящего в то же множество
, входящего в то же множество 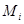 . Мы будем – по определению – полагать выполненным соотношение
. Мы будем – по определению – полагать выполненным соотношение 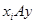 . Так определенное отношение
. Так определенное отношение 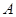 назовем отношением "быть эталоном".
назовем отношением "быть эталоном".
Легко видеть, что эквивалентность 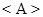 , соответствующая исходному разбиению, может быть определена так:
, соответствующая исходному разбиению, может быть определена так: 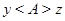 , если
, если 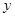 и
и 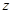 имеют общий эталон:
имеют общий эталон: 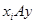 и
и 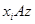 .
.
Ясно, что любое отношение эквивалентности может быть таким образом определено с помощью отношения "быть эталоном" и, наоборот, любое отношение "быть эталоном" определяет некоторую эквивалентность.
Пусть 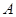 – отношение эквивалентности, а
– отношение эквивалентности, а 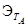 – такое отношение "быть эталоном", что
– такое отношение "быть эталоном", что 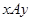 выполнено в том и только том случае, когда
выполнено в том и только том случае, когда 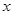 и
и 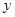 имеют общий эталон
имеют общий эталон 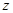 .
.
Иначе говоря, 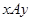 равносильно существованию такого
равносильно существованию такого 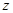 , что
, что 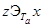 и
и 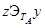 . Поскольку
. Поскольку 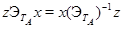 , это означает, что
, это означает, что 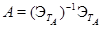 . Иначе говоря, эквивалентность можно алгебраически выразить через более простое отношение "быть эталоном". Отношение
. Иначе говоря, эквивалентность можно алгебраически выразить через более простое отношение "быть эталоном". Отношение 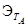 на множестве из
на множестве из 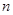 элементов можно задать графом, имеющим ровно
элементов можно задать графом, имеющим ровно 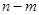 стрелок, где
стрелок, где 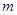 – число классов эквивалентности: каждый элемент соединяется со своим единственным эталоном. Граф, изображающий отношение эквивалентности, состоит из
– число классов эквивалентности: каждый элемент соединяется со своим единственным эталоном. Граф, изображающий отношение эквивалентности, состоит из 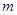 полных подграфов, содержащих по
полных подграфов, содержащих по 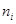 , вершин
, вершин 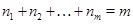 . Таким образом, общее число ребер в этом графе равно
. Таким образом, общее число ребер в этом графе равно 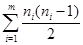 .
.
Рассмотрим в качестве 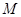 множество всех целых неотрицательных чисел и возьмем его разбиение на множество
множество всех целых неотрицательных чисел и возьмем его разбиение на множество 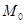 четных чисел и множество
четных чисел и множество 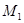 нечетных чисел. Соответствующее отношение эквивалентности на множестве целых чисел обозначается так:
нечетных чисел. Соответствующее отношение эквивалентности на множестве целых чисел обозначается так: 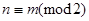 и читается:
и читается: 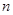 сравнимо с
сравнимо с 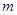 по модулю 2. В качестве эталонов здесь естественно выбрать 0 – для четных чисел и 1 – для нечетных чисел. Аналогично, разбивая то же множество
по модулю 2. В качестве эталонов здесь естественно выбрать 0 – для четных чисел и 1 – для нечетных чисел. Аналогично, разбивая то же множество 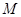 на
на 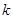 подмножеств
подмножеств 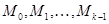 , где
, где 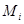 состоит из всех чисел, дающих при делении на
состоит из всех чисел, дающих при делении на 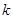 и остатке
и остатке 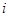 , мы придем к отношению эквивалентности:
, мы придем к отношению эквивалентности: 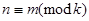 , которое выполняется, если
, которое выполняется, если 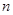 и
и 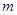 имеют одинаковый остаток при делении на
имеют одинаковый остаток при делении на 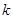 . В качестве эталона в каждом
. В качестве эталона в каждом 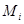 естественно выбрать соответствующий остаток
естественно выбрать соответствующий остаток 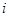 .
.
Формальные свойства эквивалентности
Мы определили выше отношении эквивалентности с помощью разбиений, т.е. фактически задали их некоторой конструкцией. Можно было бы и по-другому определить эквивалентности: можно сформулировать свойства (аксиомы), которые выделяют отношения эквивалентности среди прочих бинарных отношений.
Определение
Отношение 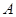 на множестве
на множестве 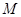 называется, эквивалентностью (или отношением эквивалентности), если оно рефлексивно, симметрично и транзитивно.
называется, эквивалентностью (или отношением эквивалентности), если оно рефлексивно, симметрично и транзитивно.
Мы сейчас дали два независимых определения одного и того же понятия. Теперь нам следует убедиться, что оба определения эквивалентпости равносильны.
Теорема. Если отношение 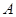 на множестве
на множестве 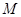 рефлексивно, симметрично и транзитивно, то существует разбиение
рефлексивно, симметрично и транзитивно, то существует разбиение 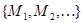 множества
множества 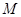 такое, что соотношение
такое, что соотношение 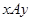 выполнено в тех и только тех случаях, когда
выполнено в тех и только тех случаях, когда 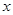 и
и 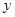 принадлежат общему классу разбиения.
принадлежат общему классу разбиения.
Обратно: если задано разбиение 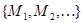 множества
множества 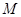 и бинарное отношение
и бинарное отношение 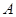 определено как "принадлежать общему классу разбиения", то
определено как "принадлежать общему классу разбиения", то 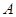 рефлексивно, симметрично и транзитивно.
рефлексивно, симметрично и транзитивно.
Доказательство первой части. Рассмотрим рефлексивное, симметричное и транзитивное отношение 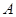 на
на 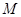 . Пусть для любого
. Пусть для любого 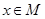 множество
множество 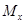 состоит из всех таких элементов
состоит из всех таких элементов 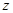 , для которых
, для которых 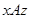 .
.
Лемма. Для любых 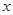 и
и 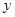 либо
либо 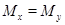 , либо
, либо 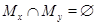 .
.
Доказательство леммы. Пусть пересечение 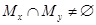 . Покажем, что
. Покажем, что 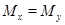 . Пусть
. Пусть 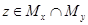 , тогда выполнено
, тогда выполнено 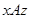 и
и 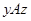 по самому определению множеств
по самому определению множеств 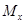 и
и 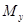 . По симметричности имеем
. По симметричности имеем 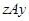 , а по транзитивности из
, а по транзитивности из 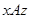 и
и 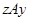 следует
следует 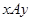 . Возьмем теперь произвольный элемент
. Возьмем теперь произвольный элемент 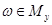 . По определению
. По определению 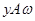 . Но из
. Но из 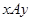 и
и 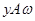 следует
следует 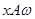 , т.е.
, т.е. 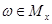 . Итак,
. Итак, 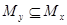 .
.
Аналогично показывается, что 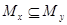 . Значит
. Значит 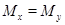 . Лемма доказана.
. Лемма доказана.
Из леммы и рефлексивности отношения 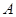 следует, что множества вида
следует, что множества вида 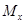 образуют разбиение множества
образуют разбиение множества 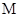 . Пусть теперь выполнено соотношение
. Пусть теперь выполнено соотношение 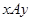 . Это значит, что
. Это значит, что 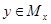 . Но и
. Но и 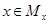 , в силу
, в силу 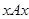 . Следовательно, оба элемента
. Следовательно, оба элемента  и
и 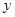 входят в
входят в 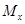 . Итак, если
. Итак, если 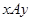 , то
, то  и
и 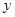 входят в общий класс разбиения. Наоборот, пусть
входят в общий класс разбиения. Наоборот, пусть 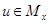 и
и 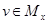 . Покажем, что
. Покажем, что 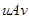 выполнено. Действительно, имеем
выполнено. Действительно, имеем 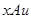 и
и 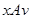 . Отсюда по симметричности
. Отсюда по симметричности 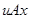 . По транзитивности из
. По транзитивности из 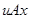 и
и 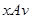 следует
следует 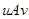 . Первая часть теоремы доказана.
. Первая часть теоремы доказана.
Доказательство второй части. Пусть дано разбиение 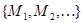 множества
множества 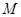 . Так как объединение всех классов разбиения совпадает с
. Так как объединение всех классов разбиения совпадает с 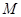 , то всякий
, то всякий 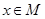 входит в некоторый класс
входит в некоторый класс 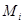 . Отсюда следует
. Отсюда следует 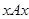 , т.е. отношение
, т.е. отношение 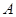 рефлексивно. Если
рефлексивно. Если 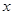 и
и 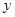 входят в класс
входят в класс 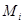 , то
, то 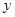 и
и  входят в тот же класс. Это означает, что из
входят в тот же класс. Это означает, что из 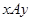 вытекает
вытекает 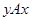 , т.е. отношение
, т.е. отношение 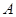 симметрично. Пусть теперь выполнено
симметрично. Пусть теперь выполнено 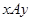 и
и 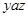 . Это означает, что
. Это означает, что  и
и 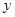 входят в класс
входят в класс 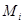 , а
, а 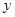 и
и 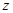 – в класс
– в класс 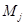 . Поскольку
. Поскольку 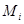 и
и 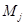 , имеют общий элемент
, имеют общий элемент 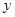 ,
, 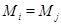 . Значит,
. Значит,  и
и 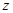 входят в
входят в 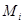 , т.е. выполнено
, т.е. выполнено 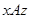 . Итак, отношение
. Итак, отношение 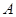 транзнтивно, чем и завершается доказательство теоремы.
транзнтивно, чем и завершается доказательство теоремы.
Теорема
Если 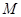 – конечное множество и
– конечное множество и 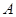 – отношение эквивалентности на нем, то существуют такие
– отношение эквивалентности на нем, то существуют такие 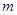 и
и 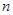 , что каждому элементу
, что каждому элементу 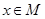 можно сопоставить кортеж (упорядоченный набор) из
можно сопоставить кортеж (упорядоченный набор) из 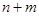 двоичных признаков (нулей или единиц):
двоичных признаков (нулей или единиц): 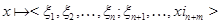 ,
, 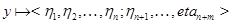 и т.д., так что 1) разным элементам соответствуют разные кортежи признаков и 2) для того, чтобы было
и т.д., так что 1) разным элементам соответствуют разные кортежи признаков и 2) для того, чтобы было 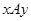 , необходимо и достаточно, чтобы первые
, необходимо и достаточно, чтобы первые 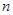 признаков этих элементов совпадали:
признаков этих элементов совпадали: 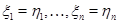 .
.
Доказательство. Возьмем разбиение 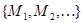 множества
множества 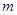 , соответствующее отношению
, соответствующее отношению 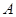 . В силу конечности множества
. В силу конечности множества 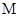 это разбиение конечно и каждый класс конечен. Перенумеруем элементы каждого класса. Тогда каждому элементу
это разбиение конечно и каждый класс конечен. Перенумеруем элементы каждого класса. Тогда каждому элементу 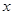 можно сопоставить пару целых чисел:
можно сопоставить пару целых чисел: 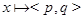 , где
, где 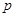 – номер класса
– номер класса 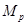 , в который попал
, в который попал  , a
, a 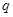 – номер элемента
– номер элемента  в своем классе. Ясно, что если
в своем классе. Ясно, что если 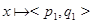 ,
, 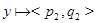 и
и 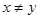 , то
, то 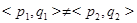 . Действительно, либо элементы
. Действительно, либо элементы  и
и 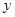 попали в разные классы – тогда у них различные первые номера;
попали в разные классы – тогда у них различные первые номера; 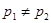 ; либо они различаются номером в классе – тогда
; либо они различаются номером в классе – тогда 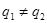 . Представим теперь числа
. Представим теперь числа 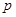 и
и 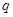 в двоичной системе счисления. Пусть
в двоичной системе счисления. Пусть 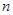 – наибольшее число разрядов у чисел
– наибольшее число разрядов у чисел 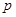 , а
, а 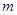 – наибольшее число разрядов у чисел
– наибольшее число разрядов у чисел 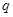 . Если некоторое
. Если некоторое 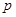 имеет меньше, чем
имеет меньше, чем 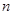 разрядов, то дополним его слева нулями. Так же поступим и со вторыми номерами. Тем самым каждому элементу будет сопоставлен кортеж из
разрядов, то дополним его слева нулями. Так же поступим и со вторыми номерами. Тем самым каждому элементу будет сопоставлен кортеж из 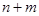 двоичных признаков.
двоичных признаков.
Для завершении доказательства достаточно заметить, что эквивалентность элементов  и
и 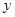 означает попадание в общий класс, т.е. совпадение первых номеров (первых
означает попадание в общий класс, т.е. совпадение первых номеров (первых 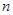 признаков).
признаков).
Эта теорема оправдывает сделанное ранее утверждение, что любая эквивалентность на конечном множестве, может быть задана как совпадение некоторого, набора общих признаков.
Итак, оба наши определения эквивалентности равносильны. Но теперь возникает вопрос, не являются ли некоторые аксиомы эквивалентности излишними. Например, быть может, из рефлексивности и симметричности уже следует транзитивность отношения?
Вернемся к обсуждению отношения 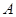 : "
: "  является эталоном для
является эталоном для 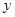 ". Мы уже дали конструктивное определение этого отношения. Из него легко можно получить следующие свойства отношения
". Мы уже дали конструктивное определение этого отношения. Из него легко можно получить следующие свойства отношения 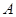 (быть эталоном):
(быть эталоном):
1) для всякого 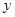 существует эталон
существует эталон  :
: 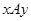 .
.
2) Если 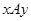 , то
, то 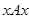 , т.е. любой эталон есть эталон для самого себя.
, т.е. любой эталон есть эталон для самого себя.
3) Эталон единствен, т.е. из 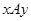 и
и 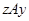 следует
следует 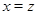 .
.
Эти три свойства можно объявить аксиомами отношения "быть эталоном". Покажем, что из них следует определение эталона с помощью разбиения. Для этого сначала по отношению 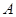 построим новое отношение
построим новое отношение 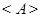 , определяемое правилом:
, определяемое правилом: 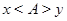 , если
, если  и
и 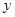 имеют общий эталон. Иначе говоря, если существует такое
имеют общий эталон. Иначе говоря, если существует такое 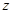 , что
, что 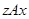 и
и 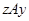 . Покажем, что
. Покажем, что 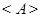 есть отношение эквивалентности. Действительно, по свойству 1) у каждого
есть отношение эквивалентности. Действительно, по свойству 1) у каждого  есть эталон и, стало быть,
есть эталон и, стало быть, 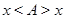 . Значит,
. Значит, 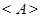 рефлексивно. Симметричность отношения
рефлексивно. Симметричность отношения 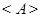 очевидна. Если
очевидна. Если 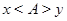 и
и 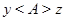 , то это значит, что
, то это значит, что  и
и 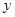 имеют общий эталон, а
имеют общий эталон, а 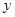 не может иметь эталона, отличного от эталона для
не может иметь эталона, отличного от эталона для 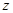 . Значит,
. Значит, 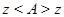 .
.
Итак, доказано, что 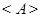 есть отношение эквивалентности. Но тогда по теореме 1.2.1 существует разбиение
есть отношение эквивалентности. Но тогда по теореме 1.2.1 существует разбиение 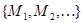 множества
множества 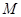 на классы эквивалентных друг другу элементов – так называемые классы эквивалентности.
на классы эквивалентных друг другу элементов – так называемые классы эквивалентности.
Очевидно, каждый класс эквивалентности 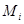 состоит из всех элементов, имеющих общий эталон
состоит из всех элементов, имеющих общий эталон 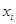 . По свойству 2)
. По свойству 2) 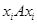 и, значит,
и, значит, 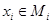 . Таким образом, отношение
. Таким образом, отношение 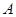 , определенное аксиоматически свойствами 1) – 3), всегда может быть задано разбиением с выбранными представителями (эталонами) в каждом классе.
, определенное аксиоматически свойствами 1) – 3), всегда может быть задано разбиением с выбранными представителями (эталонами) в каждом классе.
Пусть 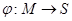 – сюръективное отображение множества
– сюръективное отображение множества 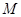 на некоторое множество
на некоторое множество 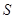 . Рассмотрим на множестве
. Рассмотрим на множестве 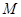 отношение "иметь общий образ" и обозначим это отношение
отношение "иметь общий образ" и обозначим это отношение 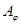 . Иначе говоря,
. Иначе говоря, 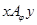 , если
, если 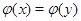 . Обозначим через
. Обозначим через 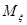 множество всех элементов
множество всех элементов 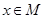 , имеющих данный образ
, имеющих данный образ 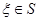 , т.е. таких, что
, т.е. таких, что 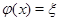 . Ясно, что
. Ясно, что 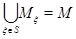 , так как любой элемент из
, так как любой элемент из 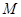 имеет образ. Далее, при разных
имеет образ. Далее, при разных 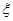 и
и 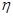 ,
, 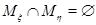 , так как иначе элемент, попавший в пересечение
, так как иначе элемент, попавший в пересечение 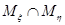 , имел бы два разных образа:
, имел бы два разных образа: 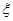 и
и 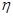 . Поскольку
. Поскольку 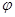 сюръективно,
сюръективно, 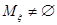 для любого
для любого 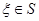 . Итак, множества
. Итак, множества 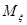 образуют разбиение множества
образуют разбиение множества 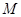 , а отношение
, а отношение 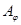 есть эквивалентность, соответствующая этому разбиению. Последнее следует из того, что
есть эквивалентность, соответствующая этому разбиению. Последнее следует из того, что 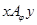 тогда и только тогда, когда
тогда и только тогда, когда  и
и 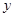 принадлежат общему, множеству
принадлежат общему, множеству 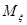 .
.
Множество классов эквивалентности по отношению 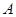 принято обозначать
принято обозначать 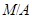 (читается: фактормножество множества
(читается: фактормножество множества 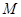 по отношению
по отношению 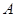 ). Наши рассуждения показывают, что для всякого сюръективного отображения
). Наши рассуждения показывают, что для всякого сюръективного отображения 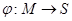 существует отношение эквивалентности
существует отношение эквивалентности 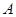 на множестве
на множестве 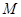 такое, что
такое, что 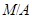 и
и 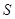 могут быть поставлены во взаимно-однозначное соответствие.
могут быть поставлены во взаимно-однозначное соответствие.
Наоборот, если имеется произвольное отношение эквивалентности 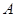 на
на 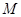 , то по нему можно построить отображение
, то по нему можно построить отображение 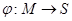 , где
, где 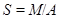 и
и 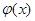 есть класс эквивалентности, содержащий
есть класс эквивалентности, содержащий  . Легко проверить, что
. Легко проверить, что 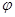 сюръективно и построенное по этому отображению отношение эквивалентности
сюръективно и построенное по этому отображению отношение эквивалентности 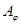 есть исходное отношение
есть исходное отношение 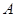 .
.
Рассмотрим частный случай, когда 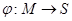 и
и 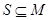 . Пусть, далее, отображение
. Пусть, далее, отображение 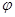 обладает тем свойством, что, при
обладает тем свойством, что, при 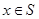 ,
, 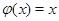 или, как говорят в таких случаях, подмножество
или, как говорят в таких случаях, подмножество 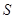 неподвижно при отображении
неподвижно при отображении 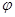 . Отсюда видно, что
. Отсюда видно, что 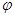 сюръективно. Действительно, всякий
сюръективно. Действительно, всякий 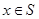 есть образ по крайней мере самого
есть образ по крайней мере самого  :
: 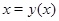 . Итак, каждому
. Итак, каждому 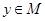 однозначно сопоставлен некоторый элемент
однозначно сопоставлен некоторый элемент 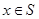 . При этом, если
. При этом, если 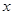 сопоставлен какому-то элементу, то самому
сопоставлен какому-то элементу, то самому  сопоставлен он же.
сопоставлен он же.
Сравнивая с соответствующими свойствами, определяющими соотношение "быть эталоном", мы видим, что отображение 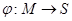 множества
множества 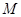 на неподвижное подмножество
на неподвижное подмножество 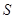 задает на
задает на 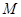 отношение
отношение 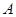 "быть эталоном" так, что
"быть эталоном" так, что 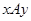 в том и только том случае, когда
в том и только том случае, когда 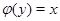 .
.
Посмотрим теперь, что получится, если отказаться от условии, что 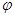 определено на всем
определено на всем 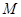 . Рассмотрим функцию
. Рассмотрим функцию 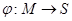 , которая некоторым элементам
, которая некоторым элементам  из
из 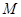 сопоставляет единственный образ
сопоставляет единственный образ 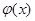 из
из 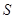 . По отображению
. По отображению 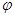 можно опять-таки построить отношение
можно опять-таки построить отношение 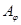 по правилу:
по правилу: 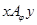 , если
, если 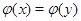 . Легко проверить, что
. Легко проверить, что 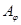 будет симметрично и транзитивно. Выберем подмножество
будет симметрично и транзитивно. Выберем подмножество 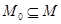 , состоящее из тех элементов, на которых определено отображение
, состоящее из тех элементов, на которых определено отображение 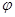 . Тогда если либо
. Тогда если либо  , либо
, либо 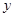 не принадлежат
не принадлежат 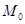 , то
, то 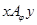 заведомо не выполняется. Значит, если
заведомо не выполняется. Значит, если  не входит в
не входит в 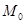 , то
, то 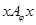 также не выполнено. Следовательно, отношение
также не выполнено. Следовательно, отношение 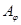 теперь уже не обязано быть рефлексивным.
теперь уже не обязано быть рефлексивным.
Видно, как построить пример симметричного и транзитивного, но не рефлексивного отношения. Пусть 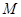 – множество людей, а отношение
– множество людей, а отношение 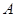 означает "быть уроженцем одного города". Легко видеть, что
означает "быть уроженцем одного города". Легко видеть, что 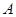 симметрично и транзитивно, но если
симметрично и транзитивно, но если  родился не в городе, а в деревне, или, вообще, во время путешествия по морю, то
родился не в городе, а в деревне, или, вообще, во время путешествия по морю, то 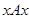 не выполнено. В этом примере
не выполнено. В этом примере 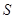 – множество городов, а отображение
– множество городов, а отображение 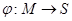 сопоставляет каждому человеку город, где он был рожден.
сопоставляет каждому человеку город, где он был рожден.
Из сказанного видно также, что условие рефлексивности можно в определении эквивалентности заменить более слабым. Достаточно потребовать, чтобы для каждого  существовал такой элемент
существовал такой элемент 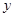 , что выполнено либо
, что выполнено либо


