Тест Голдфелда – Квандта

В данном случае предполагается, что стандартное отклонение  пропорционально значению  переменной X в этом наблюдении. Предполагается, что  имеет нормальное распределение и отсутствует автокорреляция остатков.

Тест Голдфелда – Квандта состоит в следующем:

1. Все n наблюдений упорядочиваются по величине X по возрастающей.

2. Вся упорядоченная выборка после этого разбивается на две подвыборки размерностей k, (N – 2k), k соответственно.

3. Оцениваются отдельные регрессии для первой подвыборки (k первых наблюдений) и для второй подвыборки (k последних наблюдений). Если предположение о пропорциональности дисперсий отклонений значениям X верно, то дисперсия регрессии (сумма квадратов остатков RSS₁) по первой подвыборке будет существенно меньше дисперсии регрессии (суммы квадратов остатков RSS₂) по второй подвыборке.

4. Для сравнения соответствующих дисперсий строится следующая F-статистика:

Здесь (k – m – 1) – число степеней свободы соответствующих выборочных дисперсий (m – количество объясняющих переменных в уравнении регрессии).

5. Если , то гипотеза об отсутствии гетероскедастичности отклоняется.

6. Если , то гипотеза об отсутствии гетероскедастичности принимается.

Естественным является вопрос, какими должны быть размеры подвыборок для принятия обоснованных решений. Для парной регрессии Голдфелд и Квандт предлагают следующие пропорции: n = 30, k = 11; n = 60, k = 22.

Этот же тест может быть использован при предположении об обратной пропорциональности между  и значениями объясняющей переменной. При этом F-статистика примет вид: (если X убывает).

Тест Глейзера

Тест Глейзера предполагает анализ зависимостей между дисперсиями отклонений  и значениями переменной :

В качестве зависимой переменной для изучения гетероскедастичности выбирается абсолютная величина остатков, т. е. осуществляется регрессия

где  – случайный член.

В качестве функций f обычно выбираются функции вида . Регрессия осуществляется при разных значениях γ, затем выбирается то значение, при котором коэффициент β оказывается наиболее значимым, т. е. имеет наибольшее значение t-статистики. Изменяя значения γ, можно построить различные регрессии. Обычно γ = …, -1, -0.5, 0, 0.5, 1, 1.5, … . Статистическая значимость коэффициента β в каждом конкретном случае фактически означает наличие гетероскедастичности. Если для нескольких регрессий коэффициент β оказывается статистически значимым, то при определении характера зависимости обычно ориентируются на лучшую из них.

АНАЛИЗ ДАННЫХ ПО РАСХОДАМ НА ПРЕДМЕТ НАЛИЧИЯ ГЕТЕРОСКЕДАСТИЧНОСТИ

Задача

Выполнить исследование по приведенным исходным данным, основанным на статистике США за годы с 1959-1983. Проанализировать данные на гетероскедастичность и автокорреляцию. Определить наилучшую модель из 3: линейной, степенной и гиперболической. Сделать выводы о модели.

Данные для расчета необходимо взять из табл. 1:

Таблица 1

N	Год	Текущие расходы по газу (x)	Совокупные личные расходы (y)
1	1959	74,9	70,6
2	1960	79,8	71,9
3	1961	80,9	72,6
4	1962	80,8	73,7
5	1963	80,8	74,8
6	1964	81,1	75,9
7	1965	81,4	77,2
8	1966	81,9	79,4
9	1967	81,7	81,4
10	1968	82,5	84,6
11	1969	84	88,4
12	1970	88,6	92,5
13	1971	95	96,5
14	1972	100	100
15	1973	104,5	105,7
16	1974	117,7	116,3
17	1975	140,9	125,2
18	1976	164,8	131,7
19	1977	195,6	139,3
20	1978	214,9	149,1
21	1979	249,2	162,5
22	1980	297	179
23	1981	336,8	194,5
24	1982	404,2	206
25	1983	473,4	213,6

Решение:

1. Найдем линейную модель в виде . Оценки для α и β определяем с помощью метода наименьших квадратов по формулам:

Для этого найдем:

Среднее значение x:

Среднее значение y:

Ковариацию x и y:

Вариацию x:

Вариацию y:

Тогда,

Полученная мною линейная модель имеет вид:

В результате выполнения регрессионного анализа мною получено:

TSS – полная сумма квадратов:

RSS – остаточная сумма квадратов:

ESS – оцененная модель суммы квадратов:

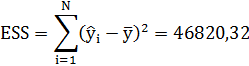
Условия правильности моих вычислений на данном этапе проверим по формуле:

TSS = ESS + RSS

49901,17 = 46820,32 + 3080,849

Вычислим коэффициент корреляции и коэффициент детерминации:

Критерием правильности решения задачи является:

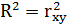
0,94 = 0,94

Данные параметры характеризуют хорошую линейную зависимость между текущими расходами и совокупными личными расходами на имеющихся статистических данных.

Найдем среднюю ошибку аппроксимации:

где

Для наглядности представим результаты графически.

 

Примечание. Прямая линия – уравнение регрессии, а точки – статистические данные.

Определим доверительный интервал для параметров α и β:

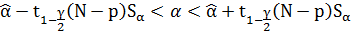
Здесь  – квантиль t-распределения Стьюдента с (N – p) степенями свободы; p – число параметров, в моем случае он равен 2;  и  – оценки исследуемых параметров, полученные ранее с использованием метода наименьших квадратов;  и  – несмещенные оценки для дисперсий случайных величин α и β; γ – уровень значимости.

Квантиль t–распределения Стьюдента с 23 степенями свободы находим из таблицы:

Для γ = 1%,  = 2,807

Для γ = 5%,  = 2,069

Доверительный интервал для 1% уровня значимости:

42,787 < α < 65,132

0,332 < β < 0,449

Доверительный интервал для 5% уровня значимости:

45,724 < α < 62,195

0,347 < β < 0,434

2. Для построения степенной модели вида необходимо привести ее к линейному виду с помощью следующего преобразования с использованием логарифмической функции: . Производя замены Y = lgy, X = lgx, A = lgα и B = β получим уравнение  , которое является уже линейным уравнением и его можно решить по аналогии с примером 1.

Вычислим параметры линейной регрессии:

Для этого найдем:

Среднее значение X:

Среднее значение Y:

Ковариацию X и Y:

 

Вариацию X:

Вариацию Y:

Тогда,

Уравнение линейной регрессии имеет вид:

 в логарифмах

Для дальнейшего анализа степенной функции необходимо выполнить обратное преобразование, то есть потенцирование полученного уравнения регрессии:

Определим:

TSS – полная сумма квадратов:

RSS – остаточная сумма квадратов:

ESS – оцененная модель суммы квадратов:

Вычислим коэффициент корреляции и коэффициент детерминации:

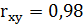
Критерием правильности решения задачи является:

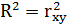
0,96 = 0,96

Найдем среднюю ошибку аппроксимации:

Определим доверительный интервал для параметров α и β:

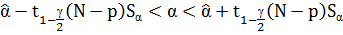
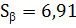
Квантиль t–распределения Стьюдента с 23 степенями свободы находим из таблицы:

Для γ = 1%,  = 2,807

Для γ = 5%,  = 2,069

Доверительный интервал для 1% уровня значимости:

-22,669 < α < 24,158

-18,812 < β < 20,031

Доверительный интервал для 5% уровня значимости:

-16,513 < α < 18,002

-13,706 < β < 14,925

3. Для построения гиперболической модели вида  необходимо привести ее к линейному виду с помощью преобразования . Производя замены Y = y, X = , A = α и B = β получим уравнение , которое является уже линейным уравнением и его можно решить по аналогии с примером 2.

Определяем параметры линейной регрессии:

Для этого найдем:

Среднее значение X:

Среднее значение Y:

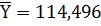
Ковариацию X и Y:

Вариацию X:

Вариацию Y:

Тогда,

Уравнение линейной регрессии имеет вид:

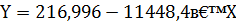
Для дальнейшего анализа гиперболической функции необходимо выполнить обратное преобразование, то есть:

Определим:

TSS – полная сумма квадратов:

RSS – остаточная сумма квадратов:

ESS – оцененная модель суммы квадратов:

Вычислим коэффициент корреляции и коэффициент детерминации:

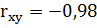
Критерием правильности решения задачи является:

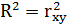
0,96 = 0,96

Найдем среднюю ошибку аппроксимации:

Определим доверительный интервал для параметров α и β:

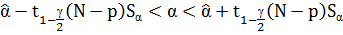
Квантиль t–распределения Стьюдента с 23 степенями свободы находим из таблицы:

Для γ = 1%,  = 2,807

Для γ = 5%,  = 2,069

Доверительный интервал для 1% уровня значимости:

203,307 < α < 230,686

-12854,8 < β < -10042

Доверительный интервал для 5% уровня значимости:

206,906 < α < 227,087

-12485,1 < β < -10411,8

При определении средней ошибки аппроксимации, я получила, что у линейной функции  = 9,4%, у степенной функции  = 6,2%, у гиперболической функции  = 5,2%. Отсюда видно, что наименьшая средняя ошибка аппроксимации равняется  = 5,2% у гиперболической функции, следовательно наилучшей моделью будет гиперболическая функция.