 |
Главная |
Уравнения первого порядка.
|
из
5.00
|
Дифференциальное уравнение называется интегрируемым в квадратурах, если его общее реше-
ние(общий интеграл) может быть получено(получен) в результате конечной последовательнос-
ти элементарных действий над известными функциями и интегрирования этих функций.
Таких уравнений сравнительно немного, рассмотрим некоторые виды дифференциальных урав-
нений, интегрируемых в квадратурах.
I. Уравнения с разделенными и разделяющимися переменными; уравнения, приводящиеся
к уравнениям с разделяющимися переменными.
Уравнение вида
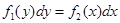 (7)
(7)
называется дифференциальным уравнением с разделенными переменными.
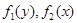 - известные непрерывные функции.
- известные непрерывные функции.
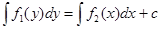 (8)
(8)
Это общий интеграл данного дифференциального уравнения (7).
Уравнение вида
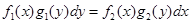 (9)
(9)
в котором коэффициенты при дифференциалах являются произведениями функций, завися-
щих только от какой-то одной переменной, называется уравнением с разделяющимися пере-
менными.
Разделим левую и правую части уравнения (9) на произведение 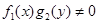 , получим урав-
, получим урав-
нение с разделенными переменными:
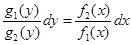 , тогда общий интеграл уравнения (9) имеет в
, тогда общий интеграл уравнения (9) имеет в
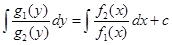 (10)
(10)
Деление на 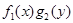 может привести к потере решений, которые обращают в ноль данное
может привести к потере решений, которые обращают в ноль данное
произведение, поэтому надо делать проверку.
Пример 5. Найти общее решение уравнения 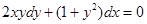 .
.
Решение. 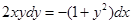 , делим левую и правую части на
, делим левую и правую части на 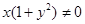 , получаем
, получаем
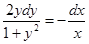 или
или 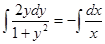 , тогда
, тогда
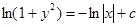 , пропотенцируем данное равенство, получим
, пропотенцируем данное равенство, получим
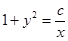 - это общий интеграл исходного уравнения.
- это общий интеграл исходного уравнения.
Уравнение вида
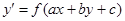 (11),
(11),
где 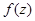 - известная непрерывная функция;
- известная непрерывная функция; 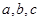 - константы, называется приводящимся к
- константы, называется приводящимся к
уравнению с разделяющимися переменными.
Чтобы привести данное уравнение к уравнению с разделяющимися переменными, надо сделать
следующую замену:
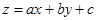 (12),
(12),
тогда 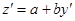 , а
, а 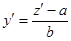 , подставляем в уравнение (11), получаем
, подставляем в уравнение (11), получаем
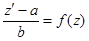 или
или 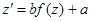 , данное уравнение является уравнением с разделяющимися
, данное уравнение является уравнением с разделяющимися
переменными, разделим переменные: 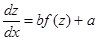 или
или 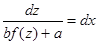 , тогда его общий интеграл имеет вид:
, тогда его общий интеграл имеет вид: 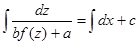 или
или 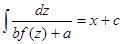 .
.
Затем заменяем 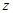 на
на 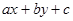 и получаем общий интеграл для уравнения (11).
и получаем общий интеграл для уравнения (11).
Пример 6. Найти общее решение уравнения 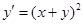 .
.
Решение. Сделаем замену 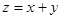 , тогда
, тогда 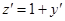 или
или 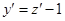 , подставляем в исходное
, подставляем в исходное
уравнение, получаем 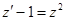 или
или 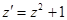 ,
, 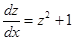 , разделяем переменные:
, разделяем переменные:
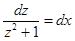 , тогда
, тогда 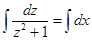 , следовательно,
, следовательно,
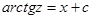 , возвращаемся к переменной
, возвращаемся к переменной 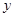 :
:
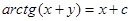 или
или 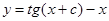 - это общее решение исходного уравнения.
- это общее решение исходного уравнения.
Лекция 2.
II. Однородные дифференциальные уравнения и приводящиеся к ним.
Определение 13. Функция 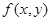 называется однородной функцией
называется однородной функцией 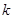 -ой степени однород-
-ой степени однород-
ности, если при любых допустимых значениях 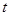 справедливо равенство
справедливо равенство
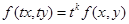 (13)
(13)
Пример 7. Рассмотрим функцию 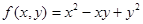 . Данная функция является однородной
. Данная функция является однородной
степени однородности 2, так как 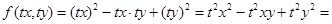
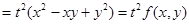 .
.
Пример 8. Функция 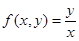 однородная степени однородности 0, так как
однородная степени однородности 0, так как
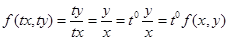 .
.
Определение 14. Уравнение 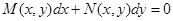 (14)
(14)
называется однородным, если функции 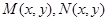 являются однородными одинаковой
являются однородными одинаковой
степени однородности.
Однородное уравнение еще может записываться следующим образом
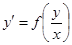 (15)
(15)
Решаются однородные дифференциальные уравнения с помощью замены:
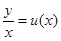 , тогда
, тогда 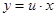 ,
, 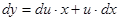 (для уравнения (14)),
(для уравнения (14)), 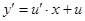 ( для уравнения
( для уравнения
(15)). После замены уравнение станет уравнением с разделяющимися переменными 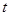 и
и 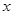 .
.
Пример 9. Найти общий интеграл уравнения 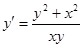 .
.
Решение. Уравнение можно записать следующим образом 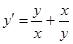 . Сделаем соответствую-щую замену и подставим в уравнение, получим:
. Сделаем соответствую-щую замену и подставим в уравнение, получим:
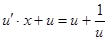 или
или 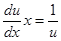 , разделяем переменные, тогда
, разделяем переменные, тогда 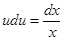 ; интегрируем
; интегрируем
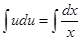 , получаем
, получаем 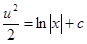 или
или 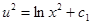 .
.
Теперь вернемся к прежней переменной 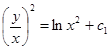 или
или 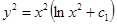 - это общий
- это общий
интеграл исходного уравнения.
Определение 15. Уравнение 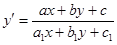 (16),
(16),
где 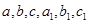 - константы, причем
- константы, причем 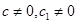 называется уравнением, приводящимся к
называется уравнением, приводящимся к
однородному.
В случае, когда 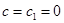 , уравнение (16) будет являться однородным.
, уравнение (16) будет являться однородным.
Рассмотрим следующие случаи:
1. 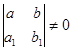
Введем новые переменные 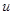 и
и 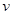 следующим образом:
следующим образом:
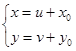 (17),
(17),
где 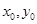 пока неопределенные константы,
пока неопределенные константы, 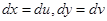 , тогда уравнение (16) примет вид
, тогда уравнение (16) примет вид
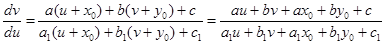
Если подобрать 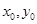 таким образом, чтобы
таким образом, чтобы
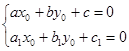 (18),
(18),
то есть 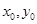 являются решением системы (18), тогда получим однородное уравнение:
являются решением системы (18), тогда получим однородное уравнение:
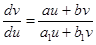 (19)
(19)
Найдем его общий интеграл, а затем вернемся к старым переменным и получим общий ин-
теграл уравнения (16).
2. 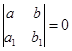 , это означает, что строки определителя пропорциональны, то есть
, это означает, что строки определителя пропорциональны, то есть
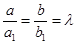 , значит уравнение (16) имеет вид:
, значит уравнение (16) имеет вид:
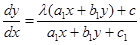 (20)
(20)
Это уравнение приводится к уравнению с разделяющимися переменными заменой
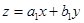 .
.
Аналогично интегрируется уравнение
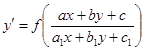 (21),
(21),
где 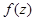 - заданная непрерывная функция.
- заданная непрерывная функция.
Пример 10. Найти общий интеграл уравнения 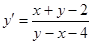 .
.
Решение. Так как 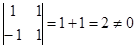 , для приведения данного уравнения к однородному
, для приведения данного уравнения к однородному
надо сделать замену, для этого сначала решим систему:
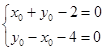 , получим
, получим 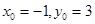 .
.
Тогда сделаем следующую замену 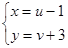 , подставляем в исходное уравнение, получаем
, подставляем в исходное уравнение, получаем
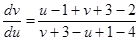 или
или 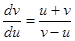 - это однородное уравнение, для его решения сделаем
- это однородное уравнение, для его решения сделаем
замену 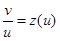 или
или 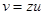 ,
, 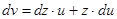 , подставляем в однородное уравнение, получа-
, подставляем в однородное уравнение, получа-
ем 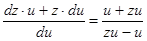 или
или 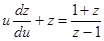 .
.
Преобразуем полученное уравнение, чтобы можно было разделить переменные:
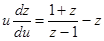
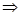
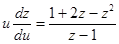
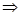
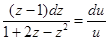 , тогда
, тогда
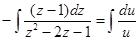
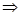
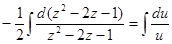
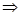
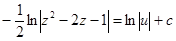 или
или 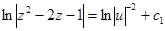 , а после потенцирования получаем
, а после потенцирования получаем
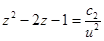 .
.
Сначала вернемся к переменной 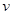 :
: 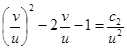 или
или 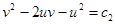 , теперь вер-
, теперь вер-
немся к переменным 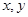 :
: 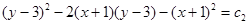 или
или
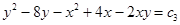 - это общий интеграл исходного уравнения.
- это общий интеграл исходного уравнения.
Пример 11. Найти общий интеграл уравнения 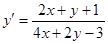 .
.
Решение. Так как 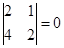 , то это уравнение, приводящееся к уравнению с разделяющимися
, то это уравнение, приводящееся к уравнению с разделяющимися
переменными. Сделаем замену 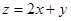 , тогда
, тогда 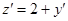 или
или 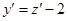 . Подставляем в
. Подставляем в
уравнение, получаем: 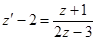 или
или 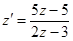 . Разделяем переменные
. Разделяем переменные 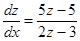 , тогда
, тогда
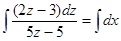
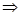
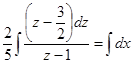
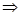
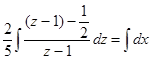
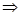
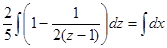
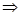
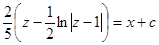 или
или 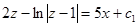 , после потен-
, после потен-
цирования получаем: 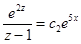 ; возвращаемся к переменной
; возвращаемся к переменной 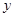 :
:
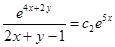 - это общий интеграл исходного уравнения.
- это общий интеграл исходного уравнения.
III. Линейные неоднородные уравнения, уравнения Бернулли.
Определение 16. Уравнение 1-ого порядка, линейное относительно неизвестной функции и
ее производной, называется линейным уравнением.
Линейное уравнение имеет вид:
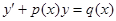 (22),
(22),
где 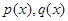 - функции, заданные на некотором промежутке
- функции, заданные на некотором промежутке 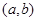 .
.
Если 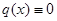 , то уравнение (22) называется линейным однородным; если
, то уравнение (22) называется линейным однородным; если 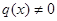 , то уравне-
, то уравне-
ние (22) называется линейным неоднородным.
Теорема 2. Если функции 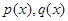 непрерывны на отрезке
непрерывны на отрезке 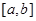 , то уравнение (22) всегда
, то уравнение (22) всегда
имеет единственное решение, удовлетворяющее начальному условию 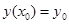 , где т.
, где т. 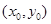
принадлежит полосе 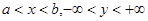 .
.
Доказательство. Разрешим уравнение (22) относительно производной, то есть в виде уравнения
(3): 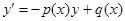 , тогда
, тогда 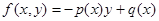 , данная функция удовлетворяет условиям
, данная функция удовлетворяет условиям
теоремы 1, а именно, она непрерывна и по переменной 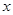 и по переменной
и по переменной 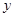 в силу условий теоремы и свойств непрерывных функций; частная производная функции по
в силу условий теоремы и свойств непрерывных функций; частная производная функции по 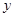 :
: 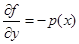 ,
,
так как частная производная непрерывна отрезке, то она ограничена на данном отрезке.
Следовательно, по теореме 1 уравнение (22) имеет единственное решение, удовлетворяющее
указанным начальным условиям.
Метод вариации произвольной постоянной.
Рассмотрим метод решения линейного неоднородного уравнения, который называется методом
вариации произвольной постоянной.
1. Сначала решаем линейное однородное уравнение, соответствующее данному неоднородному
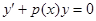
Оно одновременно является и уравнением с разделяющимися переменными, разделим перемен-
ные и проинтегрируем равенство:
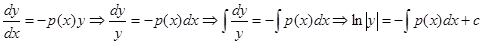 , пропотенцируем данное
, пропотенцируем данное
равенство, получим 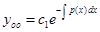 - это общее решение линейного однородного уравнения.
- это общее решение линейного однородного уравнения.
2. Теперь будем искать общее решение линейного неоднородного уравнения в виде:
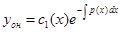 , где
, где 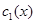 - неизвестная функция. Тогда
- неизвестная функция. Тогда 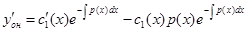
Подставляем функцию и ее производную в уравнение (22), получаем
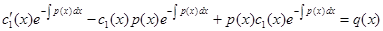 или
или 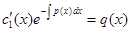 .
.
Теперь разделяем переменные и интегрируем:
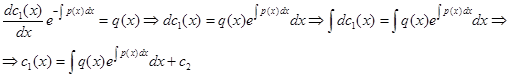
Следовательно, общее решение уравнения (22) имеет вид:
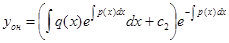 .
.
Пример 12. Найти общее решение уравнения 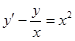 .
.
Решение. Линейное однородное уравнение, соответствующее данному неоднородному
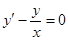 . Разделяем переменные и интегрируем:
. Разделяем переменные и интегрируем: 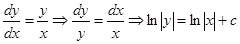 ,
,
потенцируем полученное равенство, получаем 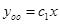 .
.
Будем искать общее решение неоднородного уравнения в виде: 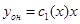 . Тогда
. Тогда
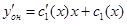 . Подставляем все в исходное уравнение, получаем:
. Подставляем все в исходное уравнение, получаем:
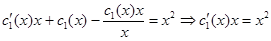 . Разделяем переменные и интегрируем
. Разделяем переменные и интегрируем
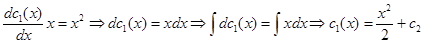 . Подставляем найденную
. Подставляем найденную
функцию, получаем общее решение линейного неоднородного уравнения
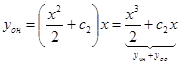 .
.
Определение 17. Уравнение вида 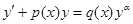 (23),
(23),
где 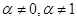 называется уравнением Бернулли.
называется уравнением Бернулли.
Сначала разделим левую и правую части уравнения (23) на 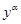 , получим
, получим
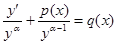 (24)
(24)
Теперь сделаем замену:
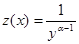 (25)
(25)
Тогда 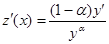 , подставляем в уравнение (24), получаем:
, подставляем в уравнение (24), получаем:
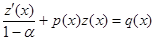 (26)
(26)
Уравнение (26) является линейным неоднородным относительно функции 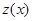 . Решаем его, а
. Решаем его, а
затем возвращаемся к переменной 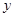 .
.
Замечание. Если 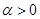 , то уравнение (23) имеет еще решение
, то уравнение (23) имеет еще решение 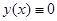 .
.
Пример 13. Найти общее решение уравнения 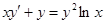 .
.
Решение. Разделим левую и правую части уравнения на 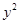 , получаем:
, получаем: 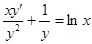 .
.
Сделаем замену 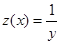 , тогда
, тогда 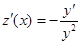 или
или 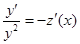 , подставляем в уравнение, полу-
, подставляем в уравнение, полу-
чаем: 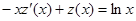 . Это линейное неоднородное уравнение. Сначала решаем линейное
. Это линейное неоднородное уравнение. Сначала решаем линейное
уравнение, соответствующее данному неоднородному, то есть 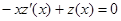 , оно является
, оно является
уравнением с разделяющимися переменными, поэтому разделяем переменные и интегрируем:
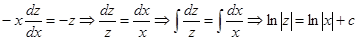 . Потенцируем полученное равенство:
. Потенцируем полученное равенство:
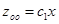 . Будем искать общее решение линейного неоднородного уравнения в виде:
. Будем искать общее решение линейного неоднородного уравнения в виде: 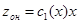 , тогда
, тогда 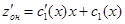 . Подставляем в неоднородное уравнение, получаем:
. Подставляем в неоднородное уравнение, получаем:
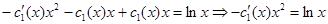 . Теперь разделяем переменные и интегрируем:
. Теперь разделяем переменные и интегрируем:
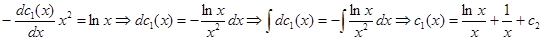 , тогда
, тогда
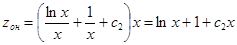 . Возвращаемся к переменной
. Возвращаемся к переменной 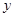 , следовательно, общее ре-
, следовательно, общее ре-
шение исходного уравнения 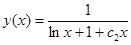 и еще одно решение, не входящее в этот на-
и еще одно решение, не входящее в этот на-
бор 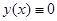 .
.
IV. Уравнения в полных дифференциалах.
Определение 18. Уравнение 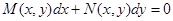 (27)
(27)
называется уравнением в полных дифференциалах, если его левая часть является полным диф-
ференциалом некоторой функции 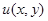 двух независимых переменных.
двух независимых переменных.
Дифференциал функции двух переменных 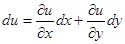 , тогда
, тогда 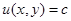 - это общий
- это общий
интеграл уравнения (27).
Теорема 3. Пусть функции 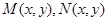 имеют непрерывные частные производные в неко-
имеют непрерывные частные производные в неко-
торой области 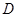 плоскости
плоскости 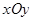 . Для того, чтобы уравнение (27) было уравнением в полных
. Для того, чтобы уравнение (27) было уравнением в полных
дифференциалах, необходимо и достаточно, чтобы выполнялось равенство
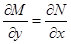 (28)
(28)
Доказательство. 1. Необходимость: пусть левая часть уравнения (27) является полным диффе-
ренциалом некоторой функции двух переменных 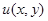 , тогда
, тогда
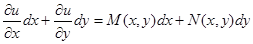 , следовательно,
, следовательно, 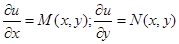 .
.
Первое равенство продифференцируем по 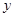 , второе – по
, второе – по 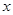 , получаем
, получаем
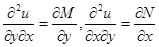 . Так как частные производные
. Так как частные производные 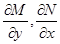 непрерывны (по условию), то
непрерывны (по условию), то
смешанные производные 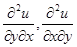 тоже непрерывны, а значит, в силу свойства смешанных
тоже непрерывны, а значит, в силу свойства смешанных
производных они равны; следовательно, выполняется равенство (28).
2. Достаточность: Пусть выполняется равенство (28); покажем, что существует функция
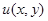 такая, что
такая, что 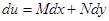 .
.
Так как в этом случае 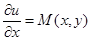 , проинтегрировав это равенство по
, проинтегрировав это равенство по 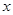 , получим
, получим
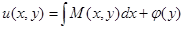 . Продифференцируем полученное равенство по
. Продифференцируем полученное равенство по 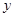 , учитываем, что
, учитываем, что
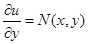 и получаем
и получаем 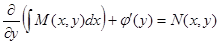 . Найдем функцию
. Найдем функцию 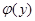 .
.
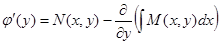 (29)
(29)
Левая часть этого равенства не зависит от 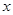 , убедимся, что и правая часть тоже не зависит
, убедимся, что и правая часть тоже не зависит
от 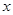 , для этого продифференцируем правую часть по
, для этого продифференцируем правую часть по 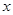 , получаем
, получаем 
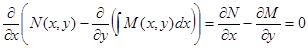 .
.
Интегрируем (29) по 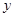 , получаем
, получаем
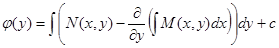 , следовательно,
, следовательно,
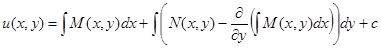 .
.
Получили искомую функцию.
Пример 14. Найти общий интеграл уравнения 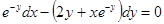 .
.
Решение. В данном уравнении 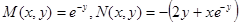 . Проверим выполнение
. Проверим выполнение
равенства (28): 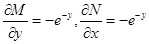 , то есть равенство (28) выполняется, следовательно,
, то есть равенство (28) выполняется, следовательно,
данное уравнение является уравнением в полных дифференциалах, левая часть уравнения –
полный дифференциал некоторой функции двух переменных 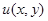 . Тогда
. Тогда 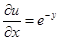 ,
,
проинтегрируем это равенство по 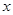 , получаем:
, получаем: 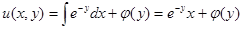 .
.
Найдем 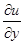 , получаем
, получаем 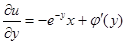 . Так как
. Так как 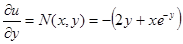 , то имеет место
, то имеет место
следующее равенство: 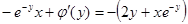 , отсюда
, отсюда 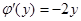 , тогда
, тогда 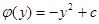 .
.
Значит общий интеграл исходного уравнения имеет вид:
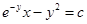 .
.
Теперь все рассмотренные уравнения 1-ого порядка и методы их решения сведем в таблицу.
Таблица 1.
| Тип уравнения 1-ого порядка | Метод решения |
1. Уравнение с разделенными переменными
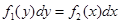
| 1. 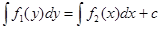 - общий интеграл - общий интеграл
|
2. Уравнение с разделяющимися перемен-
ными
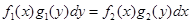
| 2. 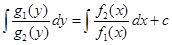 -общий интеграл
Проверка функций, удовлетворяющих
равенству -общий интеграл
Проверка функций, удовлетворяющих
равенству 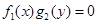
|
3. Уравнение, приводящееся к уравнению с
разделяющимися переменными
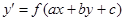
| 3. Замена 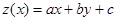 , , 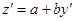
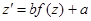
|
4. Однородное уравнение
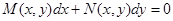 ,где ,где
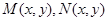 - однородные функции оди-
наковой степени однородности
или - однородные функции оди-
наковой степени однородности
или 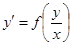
| 4. Замена 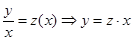 , ,
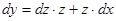 или или 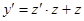
|
5. Уравнение, приводящееся к однородном 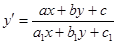 или или 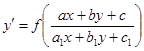
| 5. а) 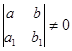 , замена , замена 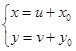 ,
где ,
где 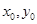 - решение системы - решение системы 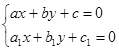 б)
б) 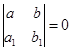 , замена , замена 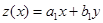
|
6. Линейное неоднородное уравнение
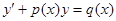
| 6. а) решается линейное однородное уравне-
ние 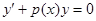 : : 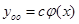 -общее решение;
б) общее решение неоднородного уравне-
ния ищется в виде -общее решение;
б) общее решение неоднородного уравне-
ния ищется в виде 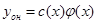
|
7. Уравнение Бернулли
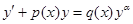 , где , где 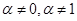
| 7. Делим на 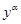 , замена , замена 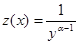 , тогда , тогда
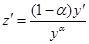 , получаем линейное неодно-
родное уравнение , получаем линейное неодно-
родное уравнение 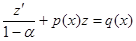
|
8. Уравнение в полных дифференциалах
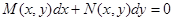 , где , где 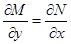
| 8. 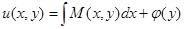 , функция , функция 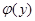 удовлетворяет уравнению
удовлетворяет уравнению
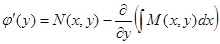
|
Лекция 3.
|
из
5.00
|
Обсуждение в статье: Уравнения первого порядка. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

