 |
Главная |
Аппроксимация и сходимость
|
из
5.00
|
Для того, чтобы выяснить, с какой точностью приблизили функцию u=u(x) с помощью функции у(х), мы должны их сравнить. Пусть uh значение функции u(х) на сеточной области 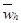 , т.е. uh
, т.е. uh 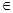 Hh.
Hh.
Рассмотрим погрешность решения разностной схемы (1.14), (1.15), которая аппроксимирует на сетке 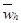 дифференциальную задачу (1.12), (1.13).
дифференциальную задачу (1.12), (1.13).
Введем функцию погрешности решения
zh=yh- uh,
где yh- решение схемы (1.14), (1.15), uh- решение задачи (1.12), (1.13) на сетке 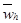 . Подставив yh = zh + uh в линейную задачу (1.14), (1.15), получим для zh задачу того же вида, что и (1.14), (1.15):
. Подставив yh = zh + uh в линейную задачу (1.14), (1.15), получим для zh задачу того же вида, что и (1.14), (1.15):
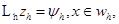 (1.26)
(1.26)
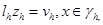 (1.27)
(1.27)
где 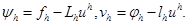 (1.28)
(1.28)
Функции (1.28) называются погрешностью аппроксимации задачи (1.12), (1.13), схемой (1.14), (1.15) на решении задачи (1.12), (1.13).
Будем говорить, что решение разностной схемы (1.14), (1.15) сходится к решению задачи (1.12), (1.13), если
при 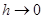
Разностная схема сходится со скоростью O(hh) или имеет n-ый порядок точности, если при достаточно малом h 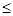 h0 выполняется неравенство
h0 выполняется неравенство
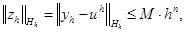
где М>0, не зависит от h, n>0.
Говорят, что разностная схема имеет n-ый порядок аппроксимации,
Если 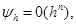
т.е. 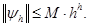
Теорема Лакса. Пусть дифференциальная задача (1.12), (1.13) поставлена корректно, разностная схема (1.14), (1.15) является корректной и аппроксимирует исходную задачу (1.12), (1.13). Тогда решение разностной схемы (1.14), (1.15) сходится к решению исходной задачи (1.12), (1.13), причем порядок точности совпадает с порядком аппроксимации.
Доказательство. Если схема (1.14), (1.15) корректна, то нетрудно получить оценку погрешности решения через погрешность аппроксимации (1.28).
Задача (1.26), (1.27) аналогична задаче (1.14), (1.15), поэтому для нее пользуясь априорной оценкой вида (1.16), получим оценку
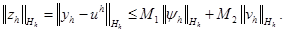 (1.29)
(1.29)
Таким образом, если схема (1.14), (1.15) корректна и аппроксимирует задачу (1.12), (1.13), то она сходится при h 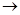 0. Норма погрешности |
0. Норма погрешности | 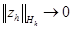 при
при
h 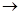 0, если
0, если 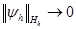 и
и 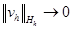 при h
при h 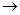 0.
0.
Из оценки (1.28) видно, что порядок точности схемы (1.14), (1.15) определяется порядком аппроксимации, и чтобы схема сходилась со скоростью O(hn), n>0 достаточно, чтобы она имела аппроксимацию того же порядка, т.е.
Рассмотрим примеры.
Пример 1. Рассмотрим явную схему Эйлера
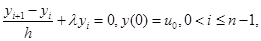
которая аппроксимирует дифференциальную задачу (1.20). Покажем порядок погрешности аппроксимации и сходимость.
Рассмотрим функцию погрешности решения 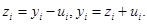
Для 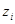 получаем схему:
получаем схему:
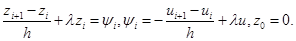 (1.30)
(1.30)
Разложим 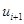 по формуле Тейлора в точке
по формуле Тейлора в точке 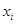 , имеем
, имеем
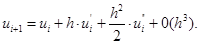 (1.31)
(1.31)
Подставляя (1.31) в 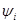 , получим
, получим 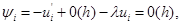 т.е. имеем первый порядок аппроксимации. Из (1.30) имеем
т.е. имеем первый порядок аппроксимации. Из (1.30) имеем
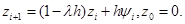
При 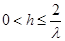 имеем
имеем 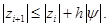 Выражая
Выражая 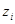 через
через 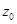 , получим:
, получим:
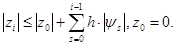
Отсюда видно, что при 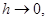
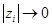 . Для точности схемы имеем
. Для точности схемы имеем
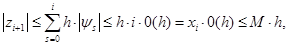 т.е. схема имеет первый порядок точности.
т.е. схема имеет первый порядок точности.
Пример 2. Рассмотрим неявную схему Эйлера
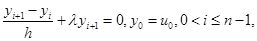
которая аппроксимирует дифференциальную задачу (1.20). Для погрешности решения 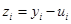 получаем разностную схему:
получаем разностную схему:
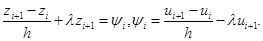
Подставляя разложение (1.31) в 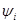 , получим
, получим
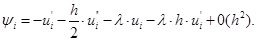
Отсюда имеем
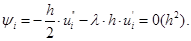
т.е. первый порядок аппроксимации. Для сходимости рассмотрим решение задачи для 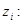
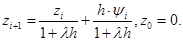
Множитель 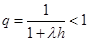 при
при 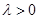 . Выражая
. Выражая 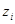 через
через 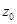 , имеем
, имеем
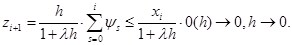
Отсюда 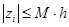 , т.е. схема имеет первый порядок точности. Таким же образом можно показать, что схема с весом
, т.е. схема имеет первый порядок точности. Таким же образом можно показать, что схема с весом
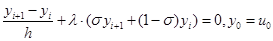
имеет первый порядок аппроксимации и при выполнении условий устойчивости имеет место сходимость и притом порядок точности совпадает с порядком погрешности аппроксимации[4].
Основные понятия и история вопроса
|
из
5.00
|
Обсуждение в статье: Аппроксимация и сходимость |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

