 |
Главная |
Схема расщепления с последовательным переходом
|
из
5.00
|
Постановка задачи.
Требуется найти функцию u(x1,x2,t), удовлетворяющую следующим условиям:
 , 0 < xα < lα , α = 1,2 (1)
, 0 < xα < lα , α = 1,2 (1)
 ,
,
x = (x1 , x2 )
u(x,0) = u0(x) , ut(x,0) = u1(x) ,  (2)
(2)
u(0, x2 ,t) = μ1- , u(l1, x2 ,t) = μ1+ (3)
u( x1 ,0,t) = μ2- , u(x1, l2 ,t) = μ2+
 l2
l2 









 X2
X2

 II
II

 I
I



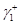


 l1
l1
0 
 X1
X1
Последовательный переход
 (4)
(4)
 (5)
(5)
Приближенным решением исходной задачи является решение задачи (5), т.е. 
Разностная схема.
Задача (4) аппроксимируется схемой

 (6)
(6)  (7)
(7)

Суммарная погрешность аппроксимации

Задача (6) решается методом правой прогонки по направлению  .
.
Решением задачи на каждом слое будет решение второй схемы (7)
Задача (6) – вспомогательная.
Стандартный вид разностных схем.
Схемы (6) и (7) сведем к стандартному виду
 , (*)
, (*)
где
по х1: 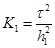 ,
, 
 1 ,
1 ,  0 ,
0 , 

 ,
,  ,
,  ,
, 
 0 ,
0 , 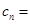 1 ,
1 , 
по х2:  ,
, 
 ,
,  ,
, 

 ,
,  ,
,  ,
, 
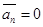 ,
,  ,
, 
Построим сетку по времени и по пространству с шагами  и h:
и h:


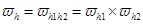



Метод правой прогонки
 ,
,  ,
, 
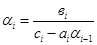 ,
,  ,
,  (**)
(**)
 ,
, 


 X2 x2
X2 x2













 | |||
 | |||


 Схема(6) Схема(7)
Схема(6) Схема(7)






0 x1 0 x1
Схема расщепления с параллельным переходом.
Постановка задачи.
Требуется найти функцию u(x1,x2,t), удовлетворяющую следующим условиям:
 , 0 < xα < lα , α = 1,2 (1)
, 0 < xα < lα , α = 1,2 (1)
 ,
,
x = (x1 , x2 )
u(x,0) = u0(x) , ut(x,0) = u1(x) ,  (2)
(2)
u(0, x2 ,t) = μ1- , u(l1, x2 ,t) = μ1+ (3)
u( x1  ,0,t) = μ2- , u(x1, l2 ,t) = μ2+
,0,t) = μ2- , u(x1, l2 ,t) = μ2+
Параллельный переход на дифференциальном уровне.
Задачи (1) - (3) расщепляем на две автономные задачи по направлениям осей координат.
 (8)
(8)
 (9)
(9)
Решение задачи определяется в виде
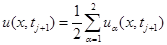
Параллельный переход на разностном уровне
 (или 0) (10)
(или 0) (10)
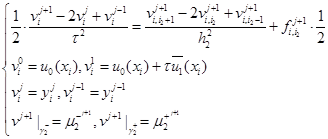 (или
(или  ) (11)
) (11)

Схема (10) решается методом правой прогонки по направлению  . Схема (11) решается методом правой прогонки по направлению
. Схема (11) решается методом правой прогонки по направлению  . Схемы (10) и (11) свести к стандартному виду (*) и решить методом правой прогонки (**).
. Схемы (10) и (11) свести к стандартному виду (*) и решить методом правой прогонки (**).

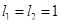 ,
,  ,
,  , Т=1.
, Т=1.

 x2 l1 x2
x2 l1 x2













 | |||
 | |||


 Схема(10) Схема(11)
Схема(10) Схема(11)





 l1
l1
0 x1 0 x1
Погрешность аппроксимации.
Погрешность аппроксимации понимаем в суммарном смысле, т.е. экономичные схемы (6) – (7) и (10) – (11) аддитивные. Покажем погрешность аппроксимации схемы (6) – (7). Для этого введем функции погрешности решения
 ,
,  ,
, 
 ,
,  (12)
(12)
Подставляем (12) в (6) и (7), имеем


где 
 .
.
Тогда
 ,
, 
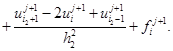
Отсюда  ,
, 
Покажем погрешность аппроксимации схемы (10) – (11). Для этого подставим (12) в (10) и (11), имеем


где 

 ,
, 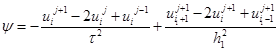

Отсюда  ,
,  .
.
Устойчивость схемы.
Устойчивость схемы (6) – (7) вычисляется по схемам (6) и (7) по отдельности устойчивы. Действительно, решение схемы (6) ищем в виде

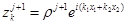 (14)
(14)
Подставим (14) в (6), имеем при 
 ,
, 
 . Отсюда
. Отсюда
 . Для устойчивости схемы должно выполнятся условие
. Для устойчивости схемы должно выполнятся условие 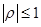 (Корни квадратного уравнения
(Корни квадратного уравнения  . Если
. Если  ). Отсюда
). Отсюда  условие
условие 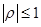 выполняется при любом
выполняется при любом  . Схема (вычислительный алгоритм) абсолютно устойчив.
. Схема (вычислительный алгоритм) абсолютно устойчив.
Аналогично покажем устойчивость схемы (7).
Решение схемы ищем в виде 
 .
.
Подставим (15) в (7), имеем  .
.
Отсюда 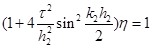

Схема (алгоритм) абсолютно устойчива. Устойчивость схем (10), (11) показываются аналогично (решаем обратное однородное уравнение, т.е.  ).
).

Заключение
Вычислительную математику в узком смысле понимают как теорию численных методов и алгоритмов решения широкого круга математических задач. В этом смысле теория разностных схем – это раздел вычислительной математики, изучающий методы приближенного решения дифференциальных уравнений путем их замены конечно – разностными уравнениями (разностными схемами). Такое понимание вычислительной математики получило распространение на первоначальном этапе развития вычислительной математики. В связи с интенсивным развитием вычислительной техники и ее использованием во всех отраслях народного хозяйства, вычислительную математику в широком смысле определяют как раздел математики, включающий круг вопросов, связанных с использованием ЭВМ.
Крупнейшим достижением вычислительной математики второй половины XX века является разработка экономичных методов решения многомерных краевых задач математической физики.
Экономичные разностные схемы подразделяются на факторизованные и аддитивные. В факторизованных схемах аппроксимацию исходной дифференциальной задачи понимают в обычном смысле, в аддитивных – в суммарном смысле.
В данной работе проведено теоретическое исследование разностных схем расщепления для первой краевой задачи двумерного уравнения колебания.
Для достижения цели исследования была решена следующая задача:
- рассмотрены методы расщепления для двумерного уравнения колебания.
Рассматриваем решение разностных задач методом правой прогонки.
Аддитивная схема обладает суммарной аппроксимацией, если каждая схема номера
Исследованы аппроксимация и устойчивость аддитивной схемы. Рассмотренные аддитивные схемы отличны от ранее рассмотренных схем и поэтому в некотором смысле являются новыми.
Список использованной литературы
1. Самарский А.А. Теория разностных схем.М.:Наука,1977.
2. Охлопков Н.М. Методологические вопросы теории и практики разностных схем.Иркутск:ИГУ,1989.
3. Охлопков Н.М., Охлопков Г.Н. Введение в специальность “Прикладная математика” ч.1. Якутск: Изд-во ЯГУ, 1997.
4. Охлопков Н.М., Охлопков Г.Н. Введение в специальность “Прикладная математика” ч.2. Якутск: Изд-во ЯГУ, 1997.
5. Охлопков Н.М. Численные методы решения обыкновенных дифференциальных уравнений. Якутск: Изд-во ЯГУ, 1993.
6. Охлопков Н.М. Численные методы решения краевых задач математической физики. Якутск: Изд-во ЯГУ, 1993.
7. Охлопков Н.М. О некоторых разностных методах решения задач для дифференциальных уравнений. Иркутск:ИГУ,1986.
8. Охлопков Н.М. Метод целых шагов решения многомерных нестационарных задач математической физики. Иркутск:ИГУ,1983.
9. Охлопков Н.М. Об экономичных методах решения задач математической физики. Якутск,ЯГУ,1982.
10. Охлопков Н.М., Николаев В.Е. Модульная технология решения задач математической физики. Иркутск:ИГУ,1989.
11. Охлопков Н.М., Николаев В.Е. Пакет программ численного решения задач математической физики.ч.2.Якутск,ЯГУ,1989.
12. Охлопков Н.М. Методологические и технологические вопросы прикладной и вычислительной математики. Якутск,1991.
13. Охлопков Н.М. Методические разработки по модульному анализу задач для дифференциальных уравнений. Якутск,ЯГУ,1996.
Методы расщепления
|
из
5.00
|
Обсуждение в статье: Схема расщепления с последовательным переходом |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

