Метод уточнения корней

 

Методы отделения корней весьма удобны и просты. Однако они дают ответ только на вопрос локализации корня и позволяют найти приближённое значение. Если же требуется найти более точное значение корня, то используют различные методы уточнении.

 

Метод половинного деления

 

Для данного метода нужен отрезок [a;b] с корнем непрерывной функции f(x) внутри и точность определения корня, которая задаётся “e”

 

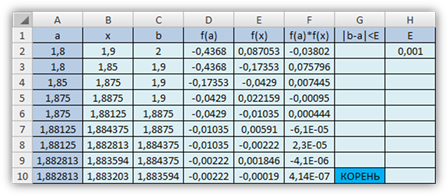
Реализация метода в пакете Excel.

Реализация метода в пакете MathCad.

 

Реализация метода половинного деления в Pascal

Блок-схема

 

 

 

Метод последовательных приближений

 

Наше уравнение 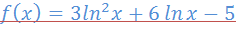 преобразуем к виду x= . Если на рассматриваемом интервале изоляции корня [1,8;2] | |<1 ,то расчётная формула примет такой вид :  , и при этом итерационный процесс приближения к корню будет сходящимся. В нашем случае выбор расчётной формулы исходного выражения очень затруднителен, поэтому воспользуемся следующим приёмом. Введём в рассмотрение произвольный параметр л>0. Тогда функция  можно представить как  .

Затем просто варьируем параметр л, добиваемся условия сходимости: | |<1 на интервале изоляции корня [1,8 ; 2]. . Для выполнения сходимости  на интервале изоляции корня [1,8; 2]. Производная исходного уравнения равна: .

Для этого примера запишем следующее:

 

.

 

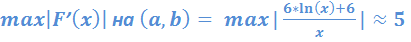Расчётная формула метода итерации примет вид:

 

 

Реализация метода в Pascal.

 

 

Метод последовательных приближений

 

Ø Реализация метода в MathCad

 

Ø Реализация метода в Excel

 

Метод Ньютона

 

Этот метод можно рассматривать как частный случай метода простой итерации и рекуррентной формулой  и тем же принципом выбора начального приближения x0. Процесс интеграции идёт до тех пор, пока . В случае неудачного выбора рекуррентной формулы получается расходящийся процесс, и условие сравнения с точностью не достигается. Для исключения подобной ситуации введём счётчик итерации n , увеличивающийся каждый раз на единицу, и поставим искусственное условие продолжения итерации в случае n<=k. В противной случае завершим алгоритм с выводом текстового сообщения о невозможности получения корня за заданное количество k шагов.

Реализация метода в MathCad

 

 

Реализация метода в Excel

 

Реализация метода в Pascal

Блок-схема.

 

 

Программа на Pascal.

 

Анализ результатов

 

Таким образом как видно из выше представленной таблицы более точные результаты корня получены в средах Excel и Pascal, хотя сам процесс уточнения был более прост и быстр в среде MathCAD. В среде MathCAD уже заложены специальные формулы, которые позволяют найти более точное значение уже со второго приближения. Уточнение корня напрямую зависит от точности его нахождения Е, чем меньше, тем точнее будет корень.

 

 

Заключение

 

Благодаря различным методам отделения и уточнения корней с любой заданной точностью, а также минимальным необходимым наборам программ, можно находить корни уравнений любой сложности. Причём это не вызывает особых затруднений, так как все операции выполняются в специальных программах. Например, в MathCAD уже заложены специальные формулы, позволяющие находить точные значения корней уравнения.

 

Список используемой литературы

1. Методическая рекомендация к выполнению курсовой работы по информатике. В.Н. Ершов

2. Общедоступная энциклопедия http://ru.wikipedia.org

3. Учебно-методическое пособие к выполнению курсовой работы “Численные методы”. В.Н. Ершов