 |
Главная |
Сохранение углов при инверсии
|
из
5.00
|
Определение. Прямые a и b назовём антипараллельными относительно  О, если
О, если  .
.

Лемма. Если  (A) =A' и
(A) =A' и  (B) =B', то прямые АВ и А'В' антипараллельны.
(B) =B', то прямые АВ и А'В' антипараллельны.
Доказательство получим, рассмотрев  ОАВ и
ОАВ и  ОА'В'.
ОА'В'.

Теорема 3. Инверсия сохраняет величину углов.
Доказательство. Пусть f и g-кривые, выходящие из точки А, f'=  (f), g'=
(f), g'=  (g) и A'=
(g) и A'=  (A).
(A).

Проводим из точки О луч, пересекающий f и g в точках В и С соответственно. Пусть B'=  (B), C'=
(B), C'=  (C). По лемме прямые АВ и А'В', АС и А'С' антипараллельны. Значит,
(C). По лемме прямые АВ и А'В', АС и А'С' антипараллельны. Значит,  OA'B'=
OA'B'=  OBA
OBA
и  OA'C'=
OA'C'=  OCA, тогда
OCA, тогда
 C'A'B'=
C'A'B'=  OA'B' -
OA'B' -  OA'C'=
OA'C'=  OBA-
OBA-  OCA=
OCA=  CAB.
CAB.
Переходя в равенстве  C'A'B'=
C'A'B'=  CAB к пределу при
CAB к пределу при  АОС
АОС  0 (луч ОС приближаем к лучу ОА), получим утверждение теоремы.
0 (луч ОС приближаем к лучу ОА), получим утверждение теоремы.
Замечание. Доказанное свойство позволяет легко строить образы прямых и окружностей при инверсии.
Пусть, например, дана прямая L и 

Проведём луч l с началом О, перпендикулярно L.
Пусть  A'=
A'=  (A).
(A).
В силу теорем 2 и 3 заключаем, что L'=  (L) - окружность с диаметром ОА'.
(L) - окружность с диаметром ОА'.
5. Инвариантные прямые и окружности
Из теоремы 2 следует, что прямые, проходящие через центр инверсии, и только они, отображаются при  на себя, т.е. эти прямые инвариантны при
на себя, т.е. эти прямые инвариантны при  .
.
Мы уже отмечали, что  ( (O,r)) = (O,r), т.е. окружность (O,r) инвариантна при
( (O,r)) = (O,r), т.е. окружность (O,r) инвариантна при  .
.
Существуют ли другие окружности, инвариантные при  ? Ответ на этот вопрос даёт следующая.
? Ответ на этот вопрос даёт следующая.
Теорема 4. Пусть S-окружность, отличная от (O,r).  (S) =S тогда и только тогда, когда S ортогональна (O,r),
(S) =S тогда и только тогда, когда S ортогональна (O,r),
Доказательство. Допустим, что  (S) =S. Ясно, что S пересекает (O,r) в двух точках, скажем, A и B.
(S) =S. Ясно, что S пересекает (O,r) в двух точках, скажем, A и B.
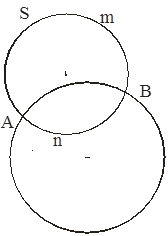
Имеем  .
.
Согласно теореме 3
( (O,r) ^  ) = ( (O,r) ^
) = ( (O,r) ^  ),
),
а это означает ортогональность S и (O,r).
Докажем обратное. Пусть теперь (O,r) ортогональна S, A и B - точки пересечения S и (O,r).
Проведём в точке А касательные к S и (O,r), которые пройдут через центры окружностей (O,r) и S соответственно.

Отсюда ясно, что S-единственная окружность, ортогональная (O,r) и проходящая через точки A и B.
Так как  (если допустить, что
(если допустить, что  , то
, то  (S) - прямая, ортогональная (O,r) и не проходящая через точку O, что невозможно), то
(S) - прямая, ортогональная (O,r) и не проходящая через точку O, что невозможно), то  (S) - окружность, ортогональная (O,r) и проходящая через точки A и B. Значит,
(S) - окружность, ортогональная (O,r) и проходящая через точки A и B. Значит,  (S) =S.
(S) =S.
Теорема 5. Окружность, проходящая через две инверсные точки, преобразуются при инверсии в себя.
Доказательство. Пусть A'=  (A), S - окружность такая, что
(A), S - окружность такая, что  и
и  . Пусть B - произвольная точка S и B'=
. Пусть B - произвольная точка S и B'=  , тогда
, тогда
 ,
,
т.е.  (B) =B', а это значит, что
(B) =B', а это значит, что
 (S) =S'.
(S) =S'.

Следствие. Окружность, проходящая через две инверсные точки, ортогональна к окружности инверсии.
Рассмотрим далее две задачи, которые нам потребуются в дальнейшем изложении.
Задача 1. Дана прямая и окружность. Найти инверсию, переводящую прямую в окружность.
Дана прямая l и окружность S с центром в точке С. Проведём (СР)
 l,
l,  .
.
Примем О за центр инверсии, тогда Р и Р' - инверсные точки, значит
r=  .
.

Итак,
 -
-
искомая инверсия, переводящая прямую в окружность.
Задача 2. Даны две окружности (  ) и (
) и (  ). Найти инверсию, переводящую одну окружность в другую.
). Найти инверсию, переводящую одну окружность в другую.
Имеет место
Теорема. Любые две неравные окружности гомотетичны и имеют внутренний и внешний центр гомотетии.

Т.к. инверсные точки, по определению, принадлежат одному лучу с вершиной в центре инверсии, то за центр инверсии выберем внешний центр гомотетии.
Пусть это точка О, тогда радиус инверсии
r=  (см. рисунок).
(см. рисунок).
|
из
5.00
|
Обсуждение в статье: Сохранение углов при инверсии |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

