 |
Главная |
Модель Пуанкаре геометрии Лобачевского на плоскости
|
из
5.00
|
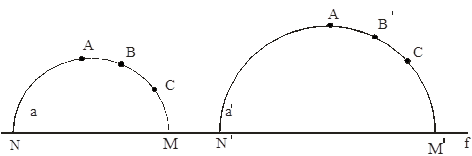
Рассмотрим евклидову плоскость и евклидову прямую f в ней. Прямая f разбивает евклидову плоскость на две полуплоскости. Выберем одну из этих полуплоскостей без её границы и назовём плоскостью Лобачевского.

Точкой Лобачевского (Л-точкой) назовём евклидову точку, принадлежащую выбранной полуплоскости без границы f.
Прямыми Лобачевского (Л - прямыми) назовём евклидовы полуокружности (в том числе и „полуокружности бесконечно большого радиуса”, ортогональные f и расположены в выбранной полуплоскости без границы.
Определим далее отношения „лежать между", „лежать на", „быть конгруэнтными" и покажем, что при этом выполняются все аксиомы геометрии Лобачевского.
Будем говорить, что Л - точка лежит на Л - прямой, если евклидова точка лежит на евклидовой полуокружности или евклидовом луче.
Проверим выполнимость аксиом принадлежности.
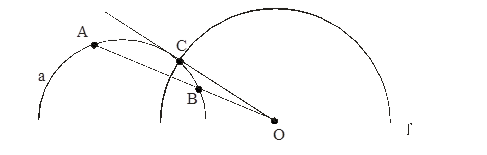
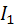 Пусть даны Л - точки А и В. Покажем, что существует Л - прямая, проходящая через эти Л - точки.
Пусть даны Л - точки А и В. Покажем, что существует Л - прямая, проходящая через эти Л - точки.

Проведём евклидову отрезку АВ срединный перпендикуляр в евклидовом смысле.
Если  то евклидова полуокружность (О, |OA|) - есть
то евклидова полуокружность (О, |OA|) - есть
Л - прямая, если  то Л - прямой будет евклидов луч.
то Л - прямой будет евклидов луч.
Из указанных построений следует выполнимость и аксиомы
 Каковы бы ни были точки А и В существует не более одной прямой, проходящей через эти две точки.
Каковы бы ни были точки А и В существует не более одной прямой, проходящей через эти две точки.
 На каждой прямой лежат по крайне мере две точки. Существуют три точки, не лежащие на одной прямой.
На каждой прямой лежат по крайне мере две точки. Существуют три точки, не лежащие на одной прямой.

Аксиома 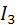 выполняется на модели, т.к это утверждение справедливо для евклидовой полуокружности и евклидова луча.
выполняется на модели, т.к это утверждение справедливо для евклидовой полуокружности и евклидова луча.
Замечание. На следующем рисунке представлена на модели
Теорема. Две прямые имеют не более одной общей точки.


Отношение „лежать между" будем понимать в обычном евклидовом смысле для точек полуокружности и луча.

Аксиомы  выполняются на модели, т.к они справедливы для евклидовых точек, евклидовых полуокружностей и лучей.
выполняются на модели, т.к они справедливы для евклидовых точек, евклидовых полуокружностей и лучей.


Проверим выполнимость аксиомы  .
.
Пусть даны Л - точки А, В, С, такие, что  ; и Л - прямая а такая, что
; и Л - прямая а такая, что 
Пусть, далее  , и имеет место ADB. Покажем, что на Л - прямой a существует Л - точка F такая, что имеет место либо BFC, либо AFC.
, и имеет место ADB. Покажем, что на Л - прямой a существует Л - точка F такая, что имеет место либо BFC, либо AFC.
Доказательство следует из теоремы: две евклидовы окружности пересекаются тогда и только тогда, когда одна из них проходит через внутреннюю точку другой окружности.

В самом деле, т.к имеет место ADB, то одна из точек А или В по отношению к окружности а внутренняя, пусть это точка В. Тогда, если точка С лежит вне окружности а, то имеет место BFC; если точка С лежит внутри окружности а, то имеет место AFC.
Замечание. На следующих рисунках представлена интерпретация отрезка, луча, угла, треугольника в плоскости Лобачевского.

[AB]

[Aa)

 (a,b)
(a,b)

ΔАВС
Прежде чем определить отношение „быть конгруэнтными", введём понятие неевклидова движения.
Пусть Л - прямая а задана в виде евклидовой полуокружности.

Симметрией Л - плоскости относительно Л - прямой а назовём инверсию евклидовой полуплоскости относительно евклидовой полуокружности.

Если Л - прямая а задана в виде евклидова луча, то будем иметь симметрию относительно евклидовой прямой.


Неевклидовым движением назовём конечную цепочку симметрий Л - плоскости относительно Л - прямых.
Будем говорить, что [AB]  [CD], если существует неевклидово движение
[CD], если существует неевклидово движение  :
:  (A) =C,
(A) =C,
 (B) =D.
(B) =D.

если существует неевклидово
движение  :
:
 (а) =с,
(а) =с,
 (b) =d.
(b) =d.
Проверим выполнимость аксиом конгруэнтности.
 Пусть дан Л - отрезок uv и Л - луч Аа. Докажем, что
Пусть дан Л - отрезок uv и Л - луч Аа. Докажем, что
1) на [Aa) существует Л - точка В такая, что [AB]  [uv] ;
[uv] ;
2) [AB]  [BA].
[BA].

рис. 1

Рис.2
Рассмотрим
 ;
;
тогда


Рассмотрим
 ,
,
тогда

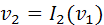 .
.
Рассмотрим
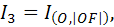 где
где  ,
,
(OF) - касательная из точки О к а, тогда
 (
( 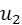 ),
), 
Из  , то цепочку симметрий оборвём и
, то цепочку симметрий оборвём и  (см. рис.1).
(см. рис.1).
Если  , то рассмотрим ещё одну симметрию
, то рассмотрим ещё одну симметрию

 -
-
касательная к а в точке А (см. рис.2).
Итак, имеем неевклидово движение 
 , преобразующее u в А, v в В, т.е.
, преобразующее u в А, v в В, т.е.
[AB] 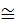 [uv].
[uv].
Докажем, что [AB] 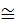 [BA].
[BA].
Рассмотрим
 , где
, где 
 - касательная из точки
- касательная из точки 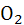 к а, тогда а= I ( a), B= I ( A), A= I ( B).
к а, тогда а= I ( a), B= I ( A), A= I ( B).
Итак, имеем неевклидово движение  , преобразующее
, преобразующее
А в В, В в А, т.е. [AB] 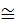 [BA].
[BA].
Прежде чем продолжить проверку аксиом конгруэнтности, рассмотрим
Замечание 1. Критерий конгруэнтности отрезков на модели Пуанкаре.

Рассмотрим упорядоченные четвёрки точек A, B, M, N и C, D, P, Q.

Доказательство.1) Пусть  . Докажем, что (ABMN) = (CDPQ).
. Докажем, что (ABMN) = (CDPQ).
Т.к.  , то существует неевклидово движение
, то существует неевклидово движение  , такое, что
, такое, что  . Остаётся показать, что
. Остаётся показать, что 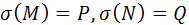 . Учитывая, что
. Учитывая, что  - конечная цепочка инверсий с центрами на f, и каждая инверсия сохраняет величину угла, имеем
- конечная цепочка инверсий с центрами на f, и каждая инверсия сохраняет величину угла, имеем  .
.
Т. к.
 , то
, то  ,
,  .
.
Итак, (ABMN) = ( CDPQ).
Пусть (ABMN) = ( CDPQ). Докажем, что  .
.

Рассмотрим
 ;
;
тогда

 ,
, 
Рассмотрим
 ;
;
тогда
 ,
, 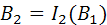 .
.
Рассмотрим  , где
, где  , (OF) - касательная из точки О к с. Тогда
, (OF) - касательная из точки О к с. Тогда  ,
,  ,
,  .
.
Покажем, что  .
.
Имеем  ,
,  , тогда (ABMN) = ( C
, тогда (ABMN) = ( C  PQ).
PQ).
Учитывая условие теоремы, получаем (CDPQ) = (C  ), откуда
), откуда  , т.е. D и
, т.е. D и  принадлежат окружности Аполлония (
принадлежат окружности Аполлония (  ), которая пересекает с в единственной точке, поэтому
), которая пересекает с в единственной точке, поэтому  .
.
Итак, существует неевклидово движение  , такое, что
, такое, что  т.е.
т.е.  .
.
Замечание 2. Критерий конгруэнтности углов на модели Пуанкаре.
Пусть  - евклидова величина неевклидова угла (а, b),
- евклидова величина неевклидова угла (а, b),  - евклидова величина неевклидова угла (c, d).
- евклидова величина неевклидова угла (c, d).
 .
.

Доказательство.1) Пусть  , тогда существует неевклидово движение
, тогда существует неевклидово движение  :
: 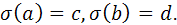
Т. к.  - это конечная цепочка инверсий, а инверсия сохраняет величину углов, то
- это конечная цепочка инверсий, а инверсия сохраняет величину углов, то  .
.
2)

Пусть  . Рассмотрим неевклидово движение
. Рассмотрим неевклидово движение  , такое, что
, такое, что 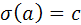 .
.
Пусть  . Если
. Если  окажется по отношению к неевклидову лучу с в той же полуплоскости, что и d, то
окажется по отношению к неевклидову лучу с в той же полуплоскости, что и d, то  , т.к инверсия сохраняет величину углов.
, т.к инверсия сохраняет величину углов.
Если же  окажется в другой полуплоскости относительно луча с, то рассмотрим инверсию
окажется в другой полуплоскости относительно луча с, то рассмотрим инверсию  .
.
Т.к. с - является биссектрисой угла (  ), то
), то  .
.
Имеем неевклидово движение  , такое, что
, такое, что  ,
,  , откуда
, откуда 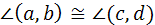 .
.
Вернёмся к проверке аксиом конгруэнтности.  . Пусть [AB]
. Пусть [AB] 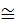 [UV], [CD]
[UV], [CD]  [UV]. Покажем, что
[UV]. Покажем, что  .
.

Т.к. [AB]  [UV], то (ABMN) = (UVLK) (1)
[UV], то (ABMN) = (UVLK) (1)
Т. к. [CD]  [UV], то (CDPQ) = (UVLK) (2)
[UV], то (CDPQ) = (UVLK) (2)
Из (1) и (2) имеем (ABMN) = (CDPQ), откуда 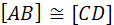
(см. критерий конгруэнтности отрезков на модели Пуанкаре).
 . Пусть имеет место ABC и
. Пусть имеет место ABC и 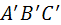 , и
, и 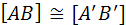 ,
,
 . Покажем, что
. Покажем, что  .
.
Т.к.  , то
, то 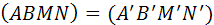 (1)
(1)
Т.к.  , то
, то  (2)
(2)
Перемножив (1) и (2), получим  , откуда
, откуда 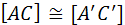 (см. критерий конгруэнтности отрезков на модели Пуанкаре).
(см. критерий конгруэнтности отрезков на модели Пуанкаре).
 . Пусть дан
. Пусть дан  и луч [Aa) с указанной полуплоскостью. Покажем, что существует единственный луч [Ab) в указанной полуплоскости, такой, что
и луч [Aa) с указанной полуплоскостью. Покажем, что существует единственный луч [Ab) в указанной полуплоскости, такой, что  ; и каждый угол конгруэнтен самому себе.
; и каждый угол конгруэнтен самому себе.

Пусть  - евклидова величина неевклидова угла (u, v).
- евклидова величина неевклидова угла (u, v).
В точке А к евклидовой полуокружности а проведём
касательную в евклидовом смысле и построим в указанной полуплоскости угол, конгруэнтный  . Получим евклидову прямую
. Получим евклидову прямую  .
.
Построим в точке А к прямой  перпендикуляр до пересечения с f в точке О. С центром в точке О, радиусом ОА проведём полуокружность.
перпендикуляр до пересечения с f в точке О. С центром в точке О, радиусом ОА проведём полуокружность.
Таким образом, получим неевклидов луч Ab.
Т.к.  , то
, то  (см. критерий конгруэнтности углов на модели Пуанкаре).
(см. критерий конгруэнтности углов на модели Пуанкаре).
Единственность луча b следует из однозначности приведённых построений.
Покажем далее, что 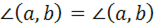 . Это следует из равенства евклидовых величин этих углов.
. Это следует из равенства евклидовых величин этих углов.
 . Пусть
. Пусть  и
и  ,
,  ,
,  ,
,  . Покажем, что
. Покажем, что  ,
,  .
.

Т.к.  , то существует неевклидово движение
, то существует неевклидово движение  , преобразующее стороны
, преобразующее стороны  в стороны
в стороны  .
.
1) Пусть  ,
,  .Т. к.
.Т. к.
 ,
,  , то
, то  ,
,  , т.е.
, т.е.  и
и  ,
,  , откуда
, откуда  ,
,  .
.
2) Пусть  ,
,  .
.
Рассмотрим инверсию  относительно биссектрисы
относительно биссектрисы  . Тогда приходим к ситуации 1).
. Тогда приходим к ситуации 1).
Замечание. На следующих рисунках изображены конгруэнтные между собой треугольники ABC и  .
.

рис. 1

рис. 2
Рассмотрим далее решение некоторых задач на модели.
Задача 1. Построить середину отрезка АВ.
1 случай

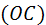 - касательная к а из О. Докажем, что
- касательная к а из О. Докажем, что  . Для этого достаточно рассмотреть
. Для этого достаточно рассмотреть 
2 случай
Строим евклидову окружность S с диаметром ОВ.



Для доказательства того, что

достаточно рассмотреть
 .
.
Заметим, что т.к.
 ,
,
то неевклидова середина отрезка АВ „тяжелее” евклидовой.
Задача 2. Построить биссектрису угла (a, b).

 - евклидовы касательные к a и b соответственно в точке А.
- евклидовы касательные к a и b соответственно в точке А.
 - евклидова биссектриса
- евклидова биссектриса
 и
и 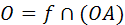 .
.
c= ( O, OA) - неевклидова биссектриса  .
.
Доказательство основано на критерии конгруэнтности углов на модели Пуанкаре.
Задача 3. Дана Л-прямая а в точке А, не лежащая на а. Построить Л-прямую b, ортогональную а, и  .
.
1 случай

Достаточно построить  и тогда b - неевклидова прямая, проходящая через точки А и
и тогда b - неевклидова прямая, проходящая через точки А и  , т.к окружность, проходящая через пару инверсных точек, ортогональна окружности инверсии.
, т.к окружность, проходящая через пару инверсных точек, ортогональна окружности инверсии.
2 случай
3 случай

( O, OA) = b
Задача 4. Построить высоту, медиану, биссектрису в треугольнике.
Решение основано на задачах 1-3.
Проверим выполнимость аксиомы непрерывности в формулировке Дедекинда.
IV. Пусть все точки прямой разбиты на два класса так, что выполняются условия:
Оба класса не пустые;
Каждая точка прямой отнесена к одному и только одному из классов;
Каждый класс есть выпуклое множество.
Покажем, что в одном из классов существует граничная точка, т.е. такая точка, которая не лежит между двумя точками одного и того же класса.
Пусть все точки Л-прямой а разбиты на два класса 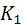 и
и  так, что выполнены условия 1-3 аксиомы Дедекинда.
так, что выполнены условия 1-3 аксиомы Дедекинда.
Рассмотрим евклидову прямую  , касающуюся Л-прямой a и параллельную f.
, касающуюся Л-прямой a и параллельную f.

Установим соответствие между точками прямых а и  , с помощью радиальных прямых. Очевидно, что это соответствие будет взаимно-однозначным. Поэтому все точки евклидовой прямой
, с помощью радиальных прямых. Очевидно, что это соответствие будет взаимно-однозначным. Поэтому все точки евклидовой прямой 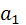 разобьются на два класса
разобьются на два класса 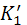 и
и  так, что будут выполнены условия 1-3 аксиом Дедекинда.
так, что будут выполнены условия 1-3 аксиом Дедекинда.
Т.к. для евклидовой прямой аксиома Дедекинда справедлива, то в одном из классов  или
или  существует граничная точка
существует граничная точка  .
.
Тогда соответствующая ей точка  будет граничной в разбиении Л-прямой а.
будет граничной в разбиении Л-прямой а.
Проверим выполнимость аксиомы Лобачевского на модели Пуанкаре.
V. Пусть дана Л-прямая а и Л-точка А, не принадлежащая а.
Покажем, что через точку А проходит, по крайне мере, две Л-прямые, не пересекающие а.
1 случай
2 случай
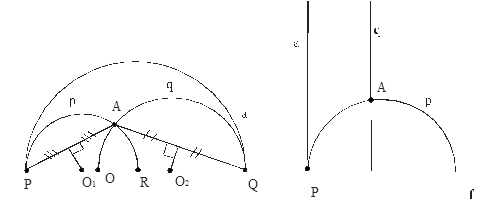
Построим евклидову полуокружность, ортогональную f и проходящую через точки P и A. Л-прямая p проходит через точку А и не пересекает а.
Аналогично строим Л-прямую q, проходящую через точку А и не пересекающую а.
Итак, существуют две Л-прямые p и q, проходящие через Л-точку А и не пересекающие Л-прямую а.
Замечание. Очевидно, что любая евклидова полуокружность, ортогональная f и проходящая через точку А и любую точку евклидова отрезка QR, не пересекает а. Таким образом, существует бесчисленное множество Л-прямых, проходящих через точку А и не пересекающих Л-прямую а.
Итак, доказана непротиворечивость геометрии Лобачевского.
В следующем параграфе покажем осуществление некоторых вопросов геометрии Лобачевского на модели Пуанкаре, где также используется инверсия.
|
из
5.00
|
Обсуждение в статье: Модель Пуанкаре геометрии Лобачевского на плоскости |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

