 |
Главная |
Определение и свойства отражающей функции
|
из
5.00
|
Министерство образования Республики Беларусь
Учреждение образования Гомельский государственный университет имени Франциска Скорины
Курсовая работа
"Семейства решений с постоянной четной частью"
Гомель, 2005
Реферат
В данной курсовой работе 17 листов. Работа состоит из пяти разделов. Ключевые слова: ДУ, решение, система, общее решение, четность, функция.
В работе содержится исследование семейства решений линейной системы. Выясняется связь семейства решений этой системы с её отражающей функцией и её свойствами. Устанавливаются условия, при которых линейная система имеет общее решение, четная часть которого не зависит от времени.
Библиография – 5 названий.
Содержание
Введение
1. Определение и свойства отражающей функции
2. Простейшая система
3. Система чет-нечет
4. Примеры систем, семейства решений которых имеют постоянную четную часть
5. Семейства решений с постоянной четной частью
Заключение
Литература
Введение
Основным инструментом нашего исследования является понятие «отражающей функции».
При изучении вопросов существования периодических решений дифференциальных систем и уравнений используются свойства симметричности (четность, нечетность и т.п.) как функций, задающих изучаемую систему, так и самих решений.
В данной работе мы будем изучать семейства решений с постоянной четной частью, когда четная часть будет представлена в виде константы.
Исследования с помощью отражающей функции позволяет получить новые результаты даже для уже хорошо изученных линейных систем.
Определение и свойства отражающей функции
Рассмотрим систему

 , (1.1)
, (1.1)
считая, что её правая часть непрерывна и имеет непрерывные частные производные по  . Общее решение этой системы в форме Коши обозначим через
. Общее решение этой системы в форме Коши обозначим через  . Через
. Через  обозначим интервал существования решения
обозначим интервал существования решения 
Пусть
 .
.
Определение: Отражающей функцией системы (1.1) назовем дифференцируемую функцию 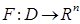 , определяемую формулой
, определяемую формулой  (*) или формулами
(*) или формулами  .
.
Для отражающей функции справедливы свойства:
1). Для любого решения  , системы
, системы  верно тождество
верно тождество
 ; (1.2)
; (1.2)
2). Для отображающей функции 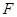 любой системы выполнены тождества:
любой системы выполнены тождества:
 ; (1.3)
; (1.3)
3). Дифференцируемая функция  будет отражающей функцией системы (1.1)тогда и только тогда, когда она удовлетворяет уравнениям в частных производных
будет отражающей функцией системы (1.1)тогда и только тогда, когда она удовлетворяет уравнениям в частных производных
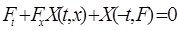 (1.4)
(1.4)
и начальному условию
 . (1.5)
. (1.5)
Уравнение (1.4) будем называть основным уравнением (основным соотношением) для отражающей функции.
► Свойство 1) следует непосредственно из определения (*). Для доказательства свойства 2) заметим, что согласно свойству 1) для любого решения 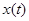 системы (1) верны тождества
системы (1) верны тождества  . Из этих тождеств в силу того, что через каждую точку
. Из этих тождеств в силу того, что через каждую точку  проходит некоторое решение
проходит некоторое решение 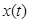 системы (1.1), и следуют тождества (1.3).
системы (1.1), и следуют тождества (1.3).
Приступим к доказательству свойства 3). Пусть  – отражающая функция системы (1.1). Тогда для неё верно тождество (1.2). Продифференцируем это тождество по
– отражающая функция системы (1.1). Тогда для неё верно тождество (1.2). Продифференцируем это тождество по  и воспользуемся тем, что
и воспользуемся тем, что  – решение системы (1.1), и самим тождеством (1.2). Получим тождество
– решение системы (1.1), и самим тождеством (1.2). Получим тождество

из которого в силу произвольности решения  следует, что
следует, что 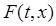 – решение системы (1.4). Начальное условие согласно свойству 2) так же выполняется.
– решение системы (1.4). Начальное условие согласно свойству 2) так же выполняется.
Пусть некоторая функция  удовлетворяет системе (1.4) и условию (1.5). Так как этой системе и этому условию удовлетворяет так же и отражающая функция, то из единственности решения задачи (1.4) – (1.5) функция
удовлетворяет системе (1.4) и условию (1.5). Так как этой системе и этому условию удовлетворяет так же и отражающая функция, то из единственности решения задачи (1.4) – (1.5) функция  должна совпадать с отражающей функцией. Свойство 3) доказано.
должна совпадать с отражающей функцией. Свойство 3) доказано.
Основная лемма. Пусть правая часть системы (1.1)  – периодична по
– периодична по 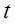 , непрерывна и имеет непрерывные частные производные по переменным
, непрерывна и имеет непрерывные частные производные по переменным 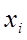 . Тогда отображение за период для системы (1.1) можно найти по формуле
. Тогда отображение за период для системы (1.1) можно найти по формуле
 ,
,
и поэтому решение  системы (1.1) будет
системы (1.1) будет  – периодическим тогда и только тогда, когда
– периодическим тогда и только тогда, когда  есть решение недифференциальной системы
есть решение недифференциальной системы
 (1.6)
(1.6)
В качестве следствия этой леммы докажем следующее предположение. Пусть непрерывно дифференцируемая функция 
 – периодична и нечетна по
– периодична и нечетна по  , т. е.
, т. е. 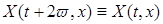 и
и  . Тогда всякое продолжение на отрезок
. Тогда всякое продолжение на отрезок  решение системы (1.1) будет
решение системы (1.1) будет  – периодическим и четным по
– периодическим и четным по 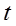 .
.
Для доказательства достаточно заметить, что функция  удовлетворяет уравнению (1.4) и условию (1.5). Поэтому она согласно свойству 3) является отражающей функцией рассматриваемой системы. Уравнение (1.6) в нашем случае вырождается в тождество, и ему удовлетворяет любое
удовлетворяет уравнению (1.4) и условию (1.5). Поэтому она согласно свойству 3) является отражающей функцией рассматриваемой системы. Уравнение (1.6) в нашем случае вырождается в тождество, и ему удовлетворяет любое  , для которого определено значение
, для которого определено значение  . Согласно основной лемме любое продолжимое на
. Согласно основной лемме любое продолжимое на  решение системы (1.1) будет
решение системы (1.1) будет 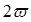 – периодическим. Четность произвольного решения
– периодическим. Четность произвольного решения  системы (1.1) следует из тождеств
системы (1.1) следует из тождеств  , справедливых в силу свойства 1) отражающей функции.
, справедливых в силу свойства 1) отражающей функции.
Простейшая система
Простейшей называют систему вида
 (2.1),
(2.1),
где  – отражающая функция этой системы.
– отражающая функция этой системы.
Теорема: Пусть  (2.2) простейшая система, тогда
(2.2) простейшая система, тогда  , где
, где  - отражающая функция системы (2.2).
- отражающая функция системы (2.2).
Если система простейшая,
 ;
;
 .
.
Замечание. Доказанная теорема позволяет нам определять, является данная нам система (2.2.) простейшей или нет. Для этого следует по системе (2.2.) записать соотношение (2.3.),из него определить функцию  , обладающую свойством
, обладающую свойством  и для неё проверить все соотношения. Если соотношения выполнены, то система простейшая.
и для неё проверить все соотношения. Если соотношения выполнены, то система простейшая.
Система чет-нечет
Рассмотрим систему
 (3.1)
(3.1)
Будем считать, что всюду в дальнейшем эта система удовлетворяет условиям:
а.) Функция  непрерывно дифференцируема, и поэтому, задача Коши для системы (3.1) имеет единственное решение;
непрерывно дифференцируема, и поэтому, задача Коши для системы (3.1) имеет единственное решение;
б.) Правая часть системы (3.1)  – периодична по
– периодична по  .
.
Лемма. Пусть система (3.1) удовлетворяет условиям а). и б). Тогда продолжимое на отрезок  решение
решение  этой системы будет
этой системы будет  – периодическим тогда и только тогда, когда
– периодическим тогда и только тогда, когда
 ,
,
где  – есть нечетная часть решения
– есть нечетная часть решения  .
.
Пусть  –
–  – периодическое решение системы (3.1). Тогда
– периодическое решение системы (3.1). Тогда  . Необходимость доказана.
. Необходимость доказана.
Пусть  – решение системы (3.1), для которого
– решение системы (3.1), для которого  . Тогда
. Тогда  , и поэтому
, и поэтому  . Таким образом, точка
. Таким образом, точка  есть неподвижная точка отображения за период, а решение
есть неподвижная точка отображения за период, а решение  –
–  – периодическое.
– периодическое.
Доказанная лемма вопрос о периодичности решения  , сводит к вычислению одного из значений нечетной части
, сводит к вычислению одного из значений нечетной части  . Иногда относительно
. Иногда относительно  можно сказать больше, чем о самом решении
можно сказать больше, чем о самом решении  . Это позволяет в таких случаях делать различные заключения относительно существования периодических решений у систем вида (3.1).Дифференцируемые функции
. Это позволяет в таких случаях делать различные заключения относительно существования периодических решений у систем вида (3.1).Дифференцируемые функции  ;
;  , удовлетворяют некоторой системе дифференциальных уравнений. Прежде, чем выписать эту систему, заметим:
, удовлетворяют некоторой системе дифференциальных уравнений. Прежде, чем выписать эту систему, заметим:
 (3.2)
(3.2)
Так как  решение системы (3.1). Заменяя в тождестве (3.2)
решение системы (3.1). Заменяя в тождестве (3.2) 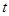 на
на 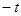 и учитывая, что производная четной функции – функция нечетная, а производная нечетной функции – функция четная, получаем тождество
и учитывая, что производная четной функции – функция нечетная, а производная нечетной функции – функция четная, получаем тождество
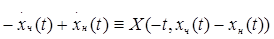 (3.3)
(3.3)
Из тождеств (3.2) и (3.3) найдем производные:
 ;
;
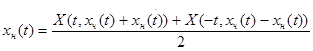 .
.
Таким образом, вектор-функция
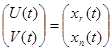 (3.4)
(3.4)
Удовлетворяет следующей системе дифференциальных уравнений порядка
 :
:  ;
;

При этом  . Систему (3.5) будем называть системой чет-нечет, соответствующей системе (3.1) решение системы чет-нечет, как следует из условия а), однозначно определяется своими начальными условиями.
. Систему (3.5) будем называть системой чет-нечет, соответствующей системе (3.1) решение системы чет-нечет, как следует из условия а), однозначно определяется своими начальными условиями.
|
из
5.00
|
Обсуждение в статье: Определение и свойства отражающей функции |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

