Теорема (обобщенное правило множителей Лагранжа).

Пусть f₀, f, g  C¹, а x* — локальное решение задачи f₀(x)  min, f(x) = , g(x)  . Тогда найдутся такие *₀  R, *  R^k, *  R^l, не равные одновременно нулю, такие, что *_j   при j  J(x*) и

*₀ f ₀(x*)+ 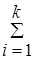*_i f _i(x*)+ 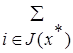*_j g_j(x*) = . (3.7)

Регулярный случай.

Так же, как и в случае ограничений-равенств, в случае общей задачи нелинейной оптимизации, необходимый признак, информативен только в случае, если *₀ . В этой ситуации, так же как и в предыдущем параграфе можно разделить (3.7) на *₀ и, следовательно, считать его равным единице. Это позволяет ввести функцию Лагранжа L: R^m×R^k×R^k  R (в регулярном случае) равенством

(x, , ) = f₀(x) + (, f(x)) + (, g(x)).

Условие регулярности в случае общей задачи выглядит сложнее. Именно, допустимая точка x называется регулярной, если векторы f ₁(x),..., f _k(x) линейно независимы и для некоторого ненулевого вектора

hR^m (f _i(x),h) = 0 при i = 1, ..., k и (g_j(x),h) < 0 при j  J(x).

Геометрически, эти условия означают, что, во-первых, вектор h является касательным к многообразию, выделяемому ограничениями-равенствами (т. е. ортогонален всем градиентам f _i(x)),и, во-вторых, он образует с градиентами g_j(x)активных ограничений (указывающими, очевидно, вовне множества ) тупой угол

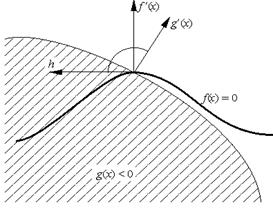
Рис. 3.3

Методы возможных направлений

Эти методы основываются на следующем простом понятии. Вектор (направление) z в допустимой точке x назовем возможным, если малое перемещение в этом направлении уменьшает значение функции f₀ и не выводит из множества допустимых точек, т. е. если при достаточно малых s точка x^s = x + sz допустима и f(x^s) < f(x). Если теперь на каждом шаге сдвигаться в возможном направлении на достаточно малое расстояние, то мы очевидно получим релаксационную последовательность, которая во многих случаях будет сходиться к решению задачи. Методы этого типа называются методами возможных направлений.

Методы проекции градиента

Проекцией P_x точки x  R^m на множество   R^m называется любая ближайшая к x точка множества :

||x  P_x||  ||x  y|| при всех y  .

В тех случаях, когда проекцию точки на множество допустимых точек найти достаточно легко (например, когда  — линейное подпространство, полупространство, шар, R^m и т. д.) используют метод проекции градиента:

xⁿ⁺¹ = P_(xⁿ  ⁿf ₀(xⁿ))

(см. рис. 3.3) являющийся прямым обобщением градиентного метода

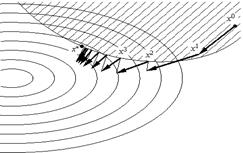
Рис. 3.4

Можно доказать, например, что если функция f₀  C¹ сильно выпукла и f  удовлетворяет условию Липшица, а множество  замкнуто и ограничено, то метод проекции градиента сходится со скоростью геометрической прогрессии.

Методы линеаризации

Суть этих методов, как следует из названия, состоит в линеаризации минимизируемой функции и ограничений в очередной точке xⁿ строящейся релаксационной последовательности и объявлении следующим значением xⁿ⁺¹ решения получающейся линейной задачи, т. е. задачи

(f ₀(xⁿ),x  xⁿ)  min, (3.8)

g_i(xⁿ) + (g_i(xⁿ),x  xⁿ)  , i = 1, ..., l. (3.9)

Чтобы эта (линейная) задача была разрешима либо добавляют штраф в минимизируемую функцию, заменяя (3.8), например, задачей

(f ₀(xⁿ), x xⁿ) + ||x  xⁿ||²  min,

либо добавляя к (20) простые ограничения, которые делают множество допустимых точек этой задачи ограниченным, например, (линейные) ограничения

x_i  xⁿ_i ⁿ  , x_i + xⁿ_i ⁿ   (i = 1, ..., m).

Методы штрафов

Основная идея здесь заключается в переходе от задачи (1), (3) к задаче безусловной оптимизации, в которой "наказывается" либо удаление от множества  допустимых точек (внешний штраф), либо приближение изнутри множества  к его границе (внутренний штраф). Различают методы внешних штрафов и внешних штрафов. При методе внешних штрафов задачу решают тем или иным методом решения безусловных задач, увеличивая на каждом шаге штраф s. Как и в случае задач с ограничениями-равенствами, основным недостатком метода штрафов является рост числа обусловленности s. На несколько другой идее основываются так называемые методы внутренних штрафов или барьеров. Образно его можно описать так: у границы множества  возводятся барьеры, не позволяющие приближаться к его границе.

Вывод: ни один метод или класс методов не выделяется своей собственной высокой эффективностью при решении оптимизационных задач различных типов, т.е. универсальностью. Инженер вынужден приспосабливать применяемый метод к конкретным характеристикам решаемой задачи.