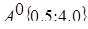Синтез оптимальной по быстродействию системы с помощью принципа максимума Понтрягина

 

Критерий управления, как отмечалось ранее, в этом случае

 

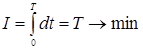 (5.1)

 

Мера ошибки в критерии H =1, а верхний предел T не известен. Начальная Х(0) = Х₀ и конечная Х(T) = Х_T точки закреплены.

Запишем функцию Гамильтона и условия трансверсальности:

 

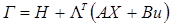
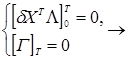
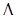(T) и 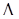 (0)-произвольны.

 

Согласно принципу максимума Понтрягина, стратегия управления состоит в минимизации функции Гамильтона относительно u. Минимум Г будет тогда, когда

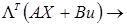 min по и

или

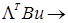 min по и

Отсюда

 

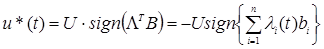 (5.2)

 

Таким образом, стратегия управления и характер u*(t) определены: оптимальное управление - это релейное управление, максимальное по величине, причем переключение управления производится тогда, когда функция 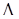^ТВ пересекает ось времени t.

По изложенной методике определим оптимальное управление 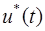, которое произвольное начальное состояние (х₁₀, x₂₀) переводит в начало координат за минимальное время Т.

Представим объект (1) в виде уравнения состояния (нормальная форма)

 

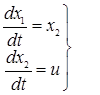 (5.3)

 

В рассматриваемом примере матрица 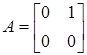, вектор 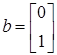. Образуем матрицу .

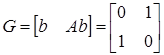Матрица G — невырожденная, поэтому система (5.3) будет нормальной. Характеристические числа матрицы A 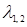= 0, поэтому система удовлетворяет условиям теоремы об n-интервалах. Оптимальное управление u*(t) является кусочно-постоянным и имеет не более двух интервалов постоянства.

Таким образом, управляющие последовательности в зависимости от начального состояния будут: {+ 1}, {-1},{+1,-1}, {-1, + 1}.

Обозначим u* = ∆=±1 и найдем общее решение системы при и* = ∆.

 

Имеем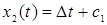

 

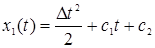
Пусть при t = 0, х₁ = х₁₀, х₂= х₂₀. Тогда, исключив время t из полученных выше равенств, найдем уравнение фазовых траекторий системы:

.

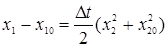Обозначим 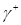 – множество начальных состояний, которые переводятся в начало координат управляющей последовательностью и*={+1}, 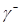– множество начальных состояний, которые переводятся в начало координат управляющей последовательностью и*={—1}. Эти множества описываются уравнениями

 

 

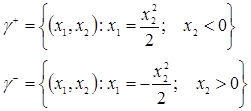
Если принять 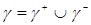 то множество  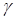запишется в виде

 

 

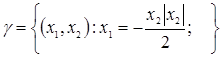
Закон управления

 

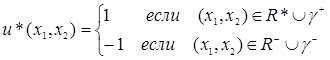 (5.4)

 

Линия 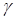 представляет собой линию переключения.

Введем функцию 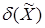, характеризующую расстояние от текущего положения фазовой точки 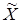(x₁,x₂) до линии переключения:

 

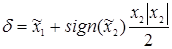 (5.5)

 

Когда фазовая точка окажется на линии переключения, то правая часть уравнения (5) будет равна нулю ( 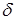 = 0) и управляющее устройство должно произвести переключение знака управления на противоположный.

Пока фазовая точка находится над линией переключения, 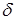 > 0 и управление должно быть отрицательным и (t) = -U .

Когда фазовая точка находится под линией переключения, 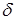 < 0 и управление должно быть положительным и (t) = +U .

Таким образом, в зависимости от знака должен выбираться и знак управления:

 

 

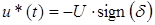
Все изложенное позволяет записать алгоритм оптимального по быстродействию регулятора для объекта (1):

 

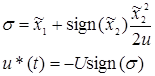
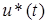=0, если 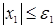, 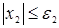х₂

 

Дано:

 

,

 

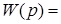
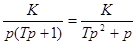где K=1, Т=1.

Решение:

Представим знаменатель дроби в виде уравнения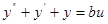

Получим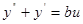

Заменим y на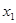

 

Получим: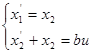

 

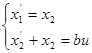
Продифференцируем уравнения

 

 

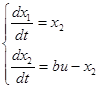
Получим

 

 

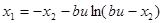
Обозначим 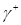 – множество начальных состояний, которые переводятся в начало координат управляющей последовательностью и*={+1}, 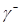– множество начальных состояний, которые переводятся в начало координат управляющей последовательностью и*={—1}. Эти множества описываются уравнениями

 

 

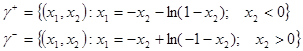
Закон управления

 

 

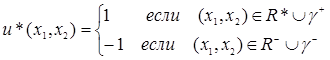
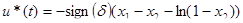
Разработаем модель для данного типа ОСАУ.

По алгоритму решения, составим структурную схему системы, реализующей выведенный закон управления.

 

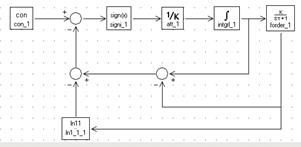
Рис. 5.1. Структурная схема модели для снятия переходной хар-ки.

 

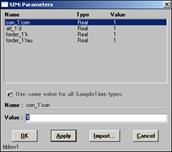
Рис. 5.2. Вводимые данные

 

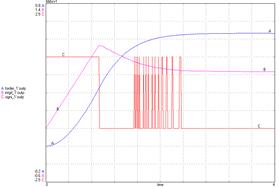
Рис. 5.3. Переходная характеристика ОСАУ

Для определения импульсной характеристики объекта необходимо изменить структуру модели решения задачи, заменив блок ступенчатого входного воздействия con, на блок pulsgen - импульсное воздействие, выходом которого является прямоугольный импульс.

При подготовке эксперимента задать параметры блока pulsgen

где: Т₁=-1 - время начала импульса;

Т₂=1 время окончания импульса;

P=1 высота импульса.

 

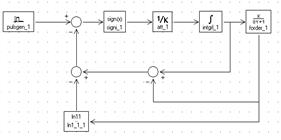
Рис. 5.4. Структурная схема модели для снятия импульсной хар-ки.

 

Рис. 5.5. Вводимые данные

 

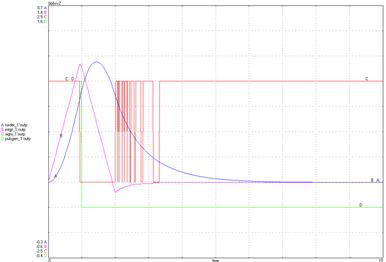
Рис. 5.6. Импульсная характеристика ОСАУ

 

Заключение

 

В теоретической части курсовой работы были рассмотрены методы поиска безусловного экстремума функции (методы прямого поиска, градиентные методы, методы второго порядка) и методы поиска экстремума функции при наличии ограничений (методы возможных направлений, методы проекции градиента, методы линеаризации, методы штрафов), указаны их основные достоинства и недостатки. В практической части произведен поиск безусловного и условного минимума несепарабельной функции двух переменных расчетным путем, выполнена алгоритмизация поиска безусловного экстремума функции двух переменных методами наискорейшего спуска и сопряженных направлений. На языке Си++ реализованы алгоритмы вышеназванных методов, а также выполнен поиск условного минимума методом симплексных процедур. Метод наискорейшего спуска для данной функции сошелся быстрее метода Зейделя-Гаусса, но для наиболее точного результата требует ввода достаточно малой величины критерия точности e. Методом симплексных процедур найден минимум функции в точке, лежащей внутри треугольника ограничений.

 

С писок литературы

 

1. Акулич И. Л. Математическое программирование в примерах и задачах. – М: Высшая школа, 1986.

2. Болтянский В. Г. Математические методы оптимального управления. – М: Наука, 1969.

3. Банди Б. Методы оптимизации (вводный курс). - М.: Радио и связь,1988.

4. Васильев Ф.П. Численные методы решения экстремальных задач. - М.: Наука, 1980.

5. Моисеев Н.Н., Иванилов Ю.П., Столяров Е.М. «Методы оптимизации», "Наука", М., 1978.

6. Полак Э. «Численные методы оптимизации», "Наука", М., 1974.

7. Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации. - М.: Наука, 1986.

8. Сеа Ж. Оптимизация. Теория и алгоритмы. - М.: Мир, 1973.

9. Поляк Б.Т. Введение в оптимизацию. - М.: Наука, 1983.

10. Цирлин А.М. «Оптимальное управление технологическими процессами»: учебное пособие для вузов. – М.:1986.-400с.

11. Чураков Е.П. «Оптимальные и адаптивные системы»: учебное пособие для вузов.-М.:1987.-256с.

12. Иванов В. А., Фалдин Н. В. Теория оптимальных систем автоматического управления. – М: Наука, 1981.

 

Приложение

Код программы метода наискорейшего спуска

#include <stdio.h>

#include <conio.h>

#include <math.h>

main ()

{

clrscr ();

float x[20];

float y[20];

float dx,dy,df,df1,df2,Fx,Fy,m1,m2,m;

int i=-1;

x[0]=0.5;

y[0]=4;

printf("---------METOD NAISKOR SPUSKA---------\n");

printf(" f(x,y)=2x^2+2xy+y^2+2x+2y+0.5\n");

printf("--------------------------------------\n");

do

{

i++;

printf("-----------A%d(%2.3f;%2.3f)------------\n",i,x[i],y[i]);

Fx=4*x[i]+2*y[i]+2;

Fy=2*x[i]+2*y[i]+2;

printf("Fx%d=%2.3f Fy%d=%2.3f\n",i,Fx,i,Fy);

m1=Fx*Fx+Fy*Fy;

m2=(4*Fx+2*Fy)*Fx+(2*Fx+2*Fy)*Fy;

m=m1/m2;

printf("mu%d=%2.3f\n",i,m);

x[i+1]=x[i]-m*Fx;

y[i+1]=y[i]-m*Fy;

dy=fabs(y[i+1]-y[i]);

dx=fabs(x[i+1]-x[i]);

df2=2*x[i+1]*x[i+1]+2*x[i+1]*y[i+1]+y[i+1]*y[i+1]+2*x[i+1]+2*y[i+1]+0.5;

df1=2*x[i]*x[i]+2*x[i]*y[i]+y[i]*y[i]+2*x[i]+2*y[i]+0.5;

df=fabs(df2-df1);

printf("delta x=%2.3f\ndelta y=%2.3f\ndelta f=%2.3f\n\n",dx,dy,df);

getch();

}

while (!((dy<0.01)&(df<0.01)&(dx<0.01)));

printf("---------------------------------------\n");

printf("iskomaya tochka A%d(%2.3f;%2.3f)",i+1,x[i+1],y[i+1]);

getch();}

 

Результат работы программы

--------METOD NAISKOR SPUSKA---------

f(x,y)=2x^2+2xy+y^2+2x+2y+0.5

-------------------------------------------

-----------A0(0.500;4.000)------------

Fx0=12.000 Fy0=11.000

mu0=0.197

delta x=2.363

delta y=2.166

delta f=26.087

-----------A1(-1.863;1.834)------------

Fx1=-1.782 Fy1=1.944

mu1=1.086

delta x=1.935

delta y=2.111

delta f=3.775

-----------A2(0.072;-0.276)------------

Fx2=1.736 Fy2=1.592

mu2=0.197

delta x=0.342

delta y=0.313

delta f=0.546

-----------A3(-0.270;-0.590)------------

Fx3=-0.258 Fy3=0.281

mu3=1.086

delta x=0.280

delta y=0.305

delta f=0.079

-----------A4(0.010;-0.895)------------

Fx4=0.251 Fy4=0.230

mu4=0.197

delta x=0.049

delta y=0.045

delta f=0.011

-----------A5(-0.039;-0.941)------------

Fx5=-0.037 Fy5=0.041

mu5=1.086

delta x=0.041

delta y=0.044

delta f=0.002

-----------A6(0.002;-0.985)------------

Fx6=0.036 Fy6=0.033

mu6=0.197

delta x=0.007

delta y=0.007

delta f=0.000

---------------------------------------

iskomaya tochka A7(-0.006;-0.991)

Код программы метода сопряженных направлений

#include <stdio.h>

#include <conio.h>

#include <math.h>

main ()

{

clrscr ();

float x[10];

float y[10];

float Fx,Fy,m1,m2,m;

int i,S1=1,S2=1;

x[0]=0.5;

y[0]=4;

printf("--------METOD SOPR. NAPRAVLENIY--------\n");

printf(" f(x,y)=2x^2+2xy+y^2+2x+2y+0.5\n");

printf("---------------------------------------\n");

for (i=0;i<2;i++)

{

printf(" A%d(%2.3f;%2.3f)\n",i,x[i],y[i]);

printf(" ---------------\n");

Fx=4*x[i]+2*y[i]+2;

Fy=2*x[i]+2*y[i]+2;

printf("S1=%d S2=%d\nFx%d=%2.3f Fy%d=%2.3f\n",S1,S2,i,Fx,i,Fy);

m1=Fx*S1+Fy*S2;

m2=(4*S1+2*S2)*S1+(2*S1+2*S2)*S2;

m=m1/m2;

printf("mu%d=%2.3f\n\n",i,m);

x[i+1]=x[i]-m*S1;

y[i+1]=y[i]-m*S2;

S1=2;

S2=-3; }

printf("---------------------------------------\n");

printf("iskomaya tochka A2(%2.3f;%2.3f)\n",x[2],y[2]);

getch();}

 

 

Результат работы программы

--------METOD SOPR. NAPRAVLENIY--------

f(x,y)=2x^2+2xy+y^2+2x+2y+0.5

---------------------------------------

A0(0.500;4.000)

---------------

S1=1 S2=1

Fx0=12.000 Fy0=11.000

mu0=2.300

A1(-1.800;1.700)

---------------

S1=2 S2=-3

Fx1=-1.800 Fy1=1.800

mu1=-0.900

---------------------------------------

iskomaya tochka A2(0.000;-1.000)

Код программы метода симплексных процедур

#include <stdio.h>

#include <conio.h>

#include <math.h>

float fun (float x,float y)

{return(2*x*x+2*x*y+y*y+2*x+2*y+0.5);}

float n1 (float x,float y)

{return(1.5*x+y-2);}

float n2 (float x,float y)

{x=x;

return(y-2);}

float n3 (float x,float y)

{return(x-y-4);}

float n4 (float x,float y)

{x=x;

return(y);}

main () {

clrscr ();

float a=2,b=1,c=1,d=1,e=1,f=0.5;

float na=1.5,nb=1.0,nc=-2.0;

float x,y,z,k,t;

int i,h=1,m;

printf("-----METOD SIMPLEX PROCEDURE-----\n");

printf(" f(x,y)=2x^2+2xy+y^2+2x+2y+0.5\n\n");

printf("1)1.5x+y-2>=0;\n2)y-2<=0;\n3)x-y<=4;\n4)y>=0\n");

printf("----------------------------------\n");

float max=0;

printf("f1(x,y,z)=2x^2+2xy+y^2+2x+2y+0.5+z(1.5x+y-2)\n");

x=((2*b*nc/nb)-2*d-2*c*nc*na+(2*e*na/nb))/(2*a-(2*b*na/nb)-na*2*b/nb+2*c*na*na);

y=(-nc/nb)-(na/nb)*x;

max=fun(x,y);

printf ("x=%2.3f\ny=%2.3f\nA%d(%2.3f;%2.3f)\n",x,y,h,x,y);

if ((n1(x,y)>=0)&(n2(x,y)<=0)&(n3(x,y)<=0)&(n4(x,y)>=0))

{printf("tochka udovl nerav f(A%d)=%2.3f\n",h,fun(x,y));

if (fun(x,y)>max) max=fun(x,y),k=x,t=y,m=h;

else max=max; }

else

printf("tochka ne udovletv neravenstvu\n");

printf("-----------------------------------\n");

na=0.0;nb=1.0;nc=-2.0;h=h+1;

printf("f2(x,y,z)=2x^2+2xy+y^2+2x+2y+0.5+z(y-2)\n");

x=((2*b*nc/nb)-2*d-2*c*nc*na+(2*e*na/nb))/(2*a-(2*b*na/nb)-na*2*b/nb+2*c*na*na);

y=(-nc/nb)-(na/nb)*x;

fun(x,y);

printf ("x=%2.3f\ny=%2.3f\nA%d(%2.3f;%2.3f)\n",x,y,h,x,y);

if ((n1(x,y)>=0)&(n2(x,y)<=0)&(n3(x,y)<=0)&(n4(x,y)>=0))

{printf("tochka udovl nerav f(A%d)=%2.3f\n",h,fun(x,y));

if (fun(x,y)>max) max=fun(x,y),k=x,t=y,m=h;

else max=max;}

else

printf("tochka ne udovletv neravenstvu\n");

printf("------------------------------------\n");

na=1.0;nb=-1.0;nc=-4.0;h=h+1;

printf("f3(x,y,z)=2x^2+2xy+y^2+2x+2y+0.5+z(x-y-4)\n");

x=((2*b*nc/nb)-2*d-2*c*nc*na+(2*e*na/nb))/(2*a-(2*b*na/nb)-na*2*b/nb+2*c*na*na);

y=(-nc/nb)-(na/nb)*x;

fun(x,y);

printf ("x=%2.3f\ny=%2.3f\nA%d(%2.3f;%2.3f)\n",x,y,h,x,y);

if ((n1(x,y)>=0)&(n2(x,y)<=0)&(n3(x,y)<=0)&(n4(x,y)>=0))

{printf("tochka udovl nerav f(A%d)=%2.3f\n",h,fun(x,y));

if (fun(x,y)>max) max=fun(x,y),k=x,t=y,m=h;

else max=max; }

else

printf("tochka ne udovletv neravenstvu\n");

printf("-------------------------------------\n");

na=0.0;nb=1.0;nc=0.0;h=h+1;

printf("f4(x,y,z)=2x^2+2xy+y^2+2x+2y+0.5+z(y)\n");

x=((2*b*nc/nb)-2*d-2*c*nc*na+(2*e*na/nb))/(2*a-(2*b*na/nb)-na*2*b/nb+2*c*na*na);

y=(-nc/nb)-(na/nb)*x;

fun(x,y);

printf ("x=%2.3f\ny=%2.3f\nA%d(%2.3f;%2.3f)\n",x,y,h,x,y);

if ((n1(x,y)>=0)&(n2(x,y)<=0)&(n3(x,y)<=0)&(n4(x,y)>=0))

{printf("tochka udovl nerav f(A%d)=%2.3f\n",h,fun(x,y));

if (fun(x,y)>max) max=fun(x,y),k=x,t=y,m=h;

else max=max; }

else

printf("tochka ne udovletv neravenstvu\n\n");

printf("---------------------------------------------\n");

printf("Nahodim znacheniya funkzii v vershinah figuri\n");

printf("---------------------------------------------\n");

x=0.0;y=2;h=h+1;

printf ("A%d(%2.3f;%2.3f)\nf%d(A%d)=%2.3f\n",h,x,y,h,h,fun(x,y));

printf ("---------------\n");

if (fun(x,y)>max) max=fun(x,y),k=x,t=y,m=h;

else max=max;

x=6.0;y=2;h=h+1;

printf ("A%d(%2.3f;%2.3f)\nf%d(A%d)=%2.3f\n",h,x,y,h,h,fun(x,y));

printf ("---------------\n");

if (fun(x,y)>max) max=fun(x,y),k=x,t=y,m=h;

else max=max;

x=4.0;y=0.0;h=h+1;

printf ("A%d(%2.3f;%2.3f)\nf%d(A%d)=%2.3f\n",h,x,y,h,h,fun(x,y));

printf ("---------------\n");

if (fun(x,y)>max) max=fun(x,y),k=x,t=y,m=h;

else max=max;

x=1.33;y=0;h=h+1;

printf ("A%d(%2.3f;%2.3f)\nf%d(A%d)=%2.3f\n",h,x,y,h,h,fun(x,y));

printf ("-----------------------------------\n");

if (fun(x,y)>max) max=fun(x,y),k=x,t=y,m=h;

else max=max;

printf("Maximalnoe znach funkzii f%d=%2.3f\nA%d(%2.3f;%2.3f)-tochka maximuma\n",m,max,m,k,t);

getch ();}

Результат работы программы

-----METOD SIMPLEX PROCEDURE-----

f(x,y)=2x^2+2xy+y^2+2x+2y+0.5

1)1.5x+y-2>=0;

2)y-2<=0;

3)x-y<=4;

4)y>=0

----------------------------------

f1(x,y,z)=2x^2+2xy+y^2+2x+2y+0.5+z(1.5x+y-2)

x=1.200

y=0.200

A1(1.200;0.200)

tochka udovl nerav f(A1)=6.700

-----------------------------------

f2(x,y,z)=2x^2+2xy+y^2+2x+2y+0.5+z(y-2)

x=-1.500

y=2.000

A2(-1.500;2.000)

tochka ne udovletv neravenstvu

------------------------------------

f3(x,y,z)=2x^2+2xy+y^2+2x+2y+0.5+z(x-y-4)

x=1.200

y=-2.800

A3(1.200;-2.800)

tochka ne udovletv neravenstvu

------------------------------------

f4(x,y,z)=2x^2+2xy+y^2+2x+2y+0.5+z(y)

x=-0.500

y=0.000

A4(-0.500;0.000)

tochka ne udovletv neravenstvu

---------------------------------------------------------

Nahodim znacheniya funkzii v vershinah figuri

---------------------------------------------------------

A5(0.000;2.000)

f5(A5)=8.500

-------------------

A6(6.000;2.000)

f6(A6)=116.500

-------------------

A7(4.000;0.000)

f7(A7)=40.500

-------------------

A8(1.330;0.000)

f8(A8)=6.698

--------------------------------------------------------------------

Maximalnoe znach funkzii f6=116.500

A6(6.000;2.000)-tochka maximuma