 |
Главная |
Моменты распределения.
|
из
5.00
|
Законы распределения случайных величин.
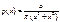 1. Закон распределения Коши.
1. Закон распределения Коши.

p(x)
x
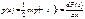 Не подчиняется условию нормировки,сл-но,редко исп-ся на прак-ке.
Не подчиняется условию нормировки,сл-но,редко исп-ся на прак-ке.
2. Лапласа.
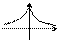
p(x)
x
3. Закон распределения Гаусса.


 P(x)
P(x)
x/σ
Подчиняется условию нормирования.
 4. Равномерный з-н распределения:если непрерывная случайная величина принимает значения лишь в пределах некоторого конечного интервала от Х1 до Х2 с постоянной функцией плотности распределения вероятностей.
4. Равномерный з-н распределения:если непрерывная случайная величина принимает значения лишь в пределах некоторого конечного интервала от Х1 до Х2 с постоянной функцией плотности распределения вероятностей.
 |
 Х1 Х2
Х1 Х2
 5. Если случайная величина изменяется синусоидально во времени, т.е. x=Xsinωt, то получаем арксинусоид. закон для функции плотности распределения вероятности.
5. Если случайная величина изменяется синусоидально во времени, т.е. x=Xsinωt, то получаем арксинусоид. закон для функции плотности распределения вероятности.

-Xm Xm
Центр распределения случайных величин.Координата центра распределения определяет положение сл.велич.на числов.оси.По отношению к погрешностям средства измерения и самим измерениям центр распределения может быть определен как центр симметрии распределения, координата центра распределения определяется по двум принципам:
1) Из принципа симметрии
р=0,5 р=0,5
слева х справа
 центр распределения
центр распределения
Такое значение х называется медианой. А сам метод – медианный.
2) Центр распределения может быть определен как центр тяжести

- мат. ожидание

- оценка мат. ожидания
Вероятностные оценки ширины распределения. Предельная и квантильная оценка
 |
Гаусса
трапециидальный закон распределения
-Хmax Xmax
 1. Предельная оценка случайной величины правомерна для равномерного, трапецеидального, треугольного, арксинусоидального распределений.Для них существует такое значение ±Xmax которое ограничивает с обеих сторон знач.случайной величины.
1. Предельная оценка случайной величины правомерна для равномерного, трапецеидального, треугольного, арксинусоидального распределений.Для них существует такое значение ±Xmax которое ограничивает с обеих сторон знач.случайной величины.
2. Квантильная оценка ширины распределения случ.величины. Кривые распределения вероятностей как правило не имеют четко выраженных границ, поэтому предельная оценка для них неправомерна. В этих случаях используется квантильная оценка случайной величины.





 р(х)
р(х)
 95%-я квантиль
95%-я квантиль
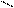 5% d 95%
5% d 95%
х
5%-я квантиль
Разделим площадь под кривой на некот.части вертик.линиями.Абсциссы таких линий наз-ся квантили.
d – интервальный промежуток. 98% всех случайных величин находится внутри этого интервального промежутка.Этот промежуток ассоциируется с вероятностью появления случайных ошибок. Δ0,9→(р=90%)-90% всех ошибок находящихся внутри этого промежутка.
Моменты распределения.
Свойство распределения в теории вероятности описывается посред-вам момента.Моменты,найденные с учетом систематической составляющей погрешности наз-ся начальными,а для центрированных распределений – центральными.

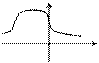
 р(х) р(х)
р(х) р(х)
истинное значение

0 Δх=(х-хц.р)
Р- системат. ошибка

 Центральным моментом k-того порядка называется выражение вида:
Центральным моментом k-того порядка называется выражение вида:
В целом, моменты систематизируются по трем признакам:
1) по порядку
2) началу отсчета (начальный или центральный)

 3) виду (дискретный, непрерывный)
3) виду (дискретный, непрерывный)
всегда
 ценр. момент
ценр. момент
 нач. момент
нач. момент


 мат.ожидание
мат.ожидание
 Дисперсия хар-ет мощность рассеяния.
Дисперсия хар-ет мощность рассеяния.
Среднее квадратичное отклонение С.К.О. количественно определяет случайную ошибку

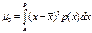 k=3 третий центр. момент - характе-ризует скошенность или асимметрию функции плотности распределения вероятности.
k=3 третий центр. момент - характе-ризует скошенность или асимметрию функции плотности распределения вероятности.
+
положительная асимметрия
-
отрицательная асимметрия

Безразмерный коэф-т асимметрии Ах вычисляется:
 k=4 – четвертый центральный момент
k=4 – четвертый центральный момент
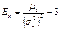 характеризует крутость распределения, т.е. островершинность или плосковершинность.
характеризует крутость распределения, т.е. островершинность или плосковершинность.
Эти свойства описываются коэффициентом эксцесса
Ех для нормального закона распределения равен 3
Ех=0 Если Ех<0,то распределение хуже по
Ex>0 отношению к норм.закону распред.
Ех>0-хорошее распределение.
Ex<0
17. Методы расчетного суммирования составляющих результиру-ющей погрешности. Дисперсия.
Задача определения расчетным путем оценки результирующей погрешности по составляющим, в метрологии, называется задачей суммирования.Практический путь: вместо многомерного закона распределения необходимо подобрать такие значения мат. ожидания, дисперсии, коэффициентов асимметрии и эксцесса, оперируя с кот. можно было бы определить числовые оценки результирующей погрешнос-ти.Правила суммирования погрешности основаны на том,что абсолютная погрешность всегда много меньше измеряемой величины,это позволяет отдельно суммировать аддитивные и мультипликативные погрешности.В пределах диапазона измерения измеряемой величины не более 10кратного измерения результирующей погрешности, может быть представлена прямой линией,а все операции расчетного суммирования необходимо проводить над среднеквадратичными отклонениями(СКО) (количественная оценка случайной погрешности)В рез-те суммир-я СКО исходных составляющих получают СКО соот-но аддитивной и мультиплик-й составляющих результирующей погр-ти.СКО аддит.состав-ей хар-ет результирующую составл-ую погр-ти в нач.диапозона измерения.А для определенияСКО результир-ей погр-ти в конце диапозонаСКО аддит. И мультип.составляющих д.б.просуммированы.
Дисперсия суммы коррелированных и некоррелированных величин. Имеется сл.величины х1и х2.Найти D(х1+х2).
D(x1+x2)=Dx1+ Dx2+ 2kx1х2; Dх1– дисперсия первой величины; Dx2 – дисперсия второй величины; 2kx1x2 – удвоенный взаимный корреляционный момент.
kx1x2=r δx1δx2 ; r(ро) – коэффициент к корреляции.
Dx1= σ2x1; Dx2= σ 2x2; σ- СКО, σ2-дисперсия
Колич.оценка суммарной величины:
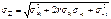
|
из
5.00
|
Обсуждение в статье: Моменты распределения. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

