 |
Главная |
Пример непрерывной функции без производной
|
из
5.00
|
Первый пример такого рода был построен Вейерштрассом; его функция определяется рядом:
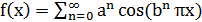 ,
,
где 0<a<1, а b есть нечетное натуральное число (причем ab>1+  π). Этот ряд мажорируется сходящейся прогрессией
π). Этот ряд мажорируется сходящейся прогрессией 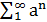 , следовательно (признаки равномерной сходимости рядов), сходится равномерно, и его сумма является всюду непрерывной функцией от x. Кропотливым исследованием Вейерштрассу удалось показать, что тем не менее ни в одной точке для нее не существует конечной производной.
, следовательно (признаки равномерной сходимости рядов), сходится равномерно, и его сумма является всюду непрерывной функцией от x. Кропотливым исследованием Вейерштрассу удалось показать, что тем не менее ни в одной точке для нее не существует конечной производной.
Здесь будет рассмотрен более простой пример ван-дер-Вардена, построенный по существу на той же идее, лишь колеблющиеся кривые у=cosωχ заменены колеблющимися ломаными.
Итак, обозначим через 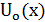 абсолютную величину разности между числом χ и ближайшим к нему целым числом. Эта функция будет линейной в каждом промежутке вида
абсолютную величину разности между числом χ и ближайшим к нему целым числом. Эта функция будет линейной в каждом промежутке вида 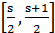 , где s-целое; она непрерывна и имеет период 1. Ее график представляет собой ломаную, он изображен на рис.1; отдельные звенья ломаной имеют угловой коэффициент ±1.
, где s-целое; она непрерывна и имеет период 1. Ее график представляет собой ломаную, он изображен на рис.1; отдельные звенья ломаной имеют угловой коэффициент ±1.
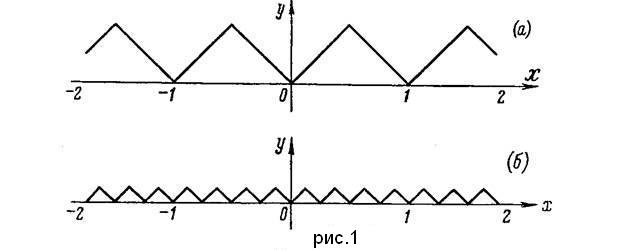

Положим, затем, для к=1,2,3,…:
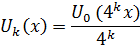
Эта функция будет линейной в промежутках вида 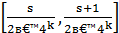 ; она также непрерывна и имеет период
; она также непрерывна и имеет период 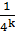 . Ее график также ломаная, но с более мелкими зубчиками; на рис.1(б), например, изображен график функции
. Ее график также ломаная, но с более мелкими зубчиками; на рис.1(б), например, изображен график функции 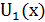 . Во всех случаях угловые коэффициенты отдельных звеньев ломаной и здесь равны ±1.
. Во всех случаях угловые коэффициенты отдельных звеньев ломаной и здесь равны ±1.
Определим теперь, для всех вещественных значений x, функцию f(x) равенством
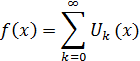
Так как, очевидно, 0≤ 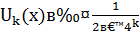 (k=0,1,2,…), так что ряд мажорируется сходящейся прогрессией
(k=0,1,2,…), так что ряд мажорируется сходящейся прогрессией 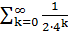 , то (как и в случае функции Вейерштрасса) ряд сходится равномерно, и функция
, то (как и в случае функции Вейерштрасса) ряд сходится равномерно, и функция 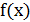 всюду непрерывна.
всюду непрерывна.
Остановимся на любом значении 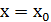 . Вычисляя его с точностью до
. Вычисляя его с точностью до 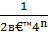 (где n=0,1,2,…), по недостатку и по избытку, мы заключим его между числами вида:
(где n=0,1,2,…), по недостатку и по избытку, мы заключим его между числами вида:
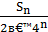 ≤
≤ 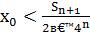 , где
, где 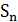 -целое.
-целое.
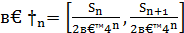 (n=0,1,2,…).
(n=0,1,2,…).
Очевидно, что замкнутые промежутки оказываются вложенными один в другой. В каждом из них найдется такая точка 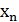 , что расстояние ее от точки
, что расстояние ее от точки 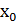 равно половине длины промежутка.
равно половине длины промежутка.
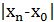 =
= 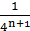 ;
;
Ясно, что с возрастанием n варианта 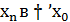 .
.
Составим теперь отношение приращений
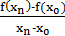 =
= 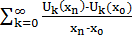
Но при k>n, число 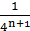 есть целое кратное периодам
есть целое кратное периодам 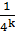 функции
функции 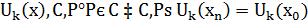 , соответствующие члены ряда обращаются в 0 и могут быть опущены. Если же k≤n, то функция
, соответствующие члены ряда обращаются в 0 и могут быть опущены. Если же k≤n, то функция 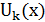 , линейная в промежутке
, линейная в промежутке 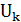 , будет линейной и в содержащемся на нем промежутке
, будет линейной и в содержащемся на нем промежутке 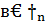 , причем
, причем
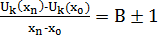 (k=0,1,…,n).
(k=0,1,…,n).
Таким образом, имеем окончательно 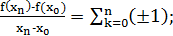 иными словами, это отношение равно четному целому числу при нечетном n и нечетному числу при четном n. Отсюда ясно, что при
иными словами, это отношение равно четному целому числу при нечетном n и нечетному числу при четном n. Отсюда ясно, что при 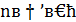 отношение приращений ни к какому конечному пределу стремится не может, так что наша функция при
отношение приращений ни к какому конечному пределу стремится не может, так что наша функция при 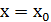 конечной производной не имеет.
конечной производной не имеет.
Решение упражнений
Упражнение 1 ([2], №909)
Функция 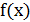 определена следующим образом:
определена следующим образом: 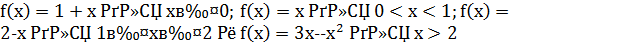 . Исследовать непрерывность
. Исследовать непрерывность 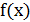 и выяснить существование
и выяснить существование 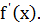
Решение
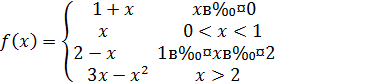
На 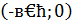
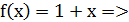 непрерывна как многочлен;
непрерывна как многочлен;
На (0;1) 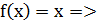 непрерывна как многочлен;
непрерывна как многочлен;
На (1;2) 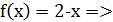 непрерывна как многочлен;
непрерывна как многочлен;
На (2; 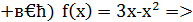 непрерывна как элементарная функция.
непрерывна как элементарная функция.
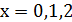 - точки подозрительные на разрыв
- точки подозрительные на разрыв
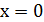
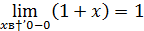
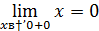
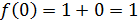
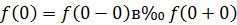
Так как левый предел равен значению функции в точке, то функция разрывна в точке 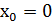 .
.
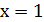
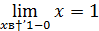
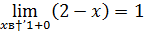
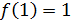
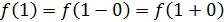
Так как левый предел равен правому пределу и равен значению функции в точке 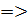 функция непрерывна в точке
функция непрерывна в точке 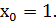
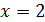
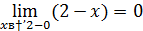
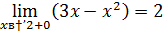
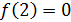
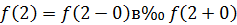
Так как левый предел равен значению функции в точке, то функция разрывна в точке 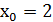 .
.
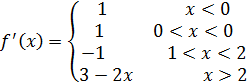
1 способ. В точке 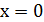 не существует конечной производной функции
не существует конечной производной функции 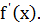 Действительно, предположим противное. Пусть в точке
Действительно, предположим противное. Пусть в точке 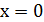 существует конечная производная функции
существует конечная производная функции 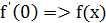 непрерывна в точке
непрерывна в точке 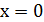 (по теореме 1: Если функция дифференцируема в точке
(по теореме 1: Если функция дифференцируема в точке  , то она непрерывна.
, то она непрерывна.
2 способ. Найдем односторонние пределы функции 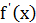 в точке x=0.
в точке x=0.
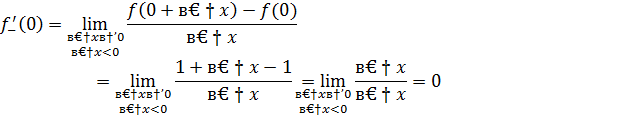
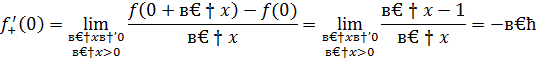
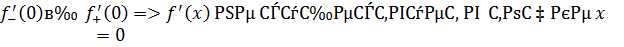
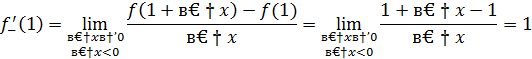
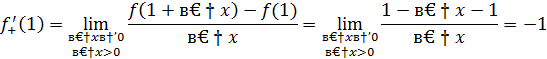
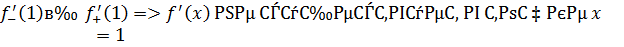
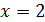
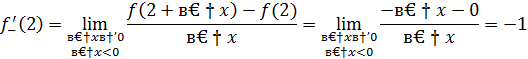
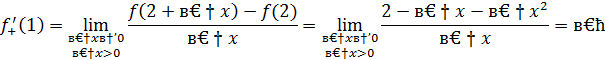
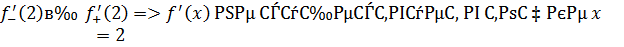
Упражнение 2 ([1], №991)
Показать, что функция 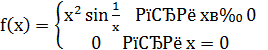 имеет разрывную производную.
имеет разрывную производную.
Решение.
Найдем производную функции.
При 
При 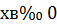
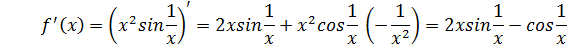
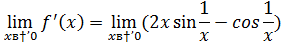
Предел 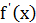 не существует
не существует 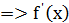 разрывна в точке
разрывна в точке 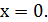
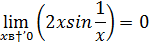
Так как 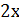 – бесконечно малая функция,
– бесконечно малая функция, 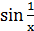 - ограниченная.
- ограниченная.
Докажем, что функция 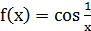 в точке
в точке 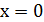 предела не имеет.
предела не имеет.
Для доказательства достаточно показать, что существуют две последовательности значений аргумента сходящиеся к 0, что 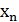 не сходится к
не сходится к 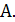
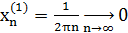
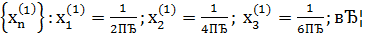
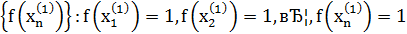
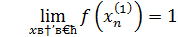
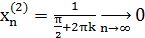
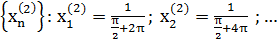
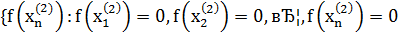
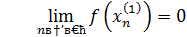
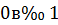
Вывод: функция 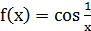 в точке
в точке 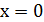 предела не имеет.
предела не имеет.
Упражнение 3 ([1], №995)
Показать, что функция 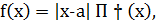 где
где 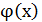 - непрерывная функция и
- непрерывная функция и 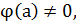 не имеет производной в точке
не имеет производной в точке 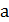 . Чему равны односторонние производные
. Чему равны односторонние производные 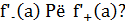
Решение.
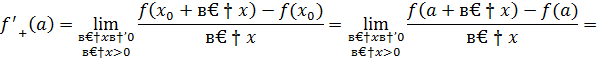
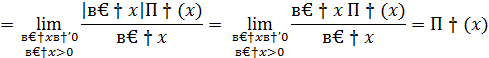
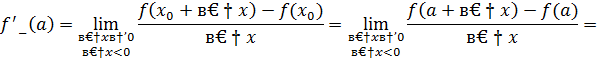
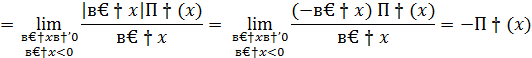
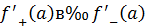
Односторонние пределы не равны  функция
функция 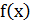 не имеет производной в точке
не имеет производной в точке 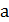 .
.
Упражнение 4 ([1], №996)
Построить пример непрерывной функции, не имеющей производной функции в данных точках: 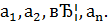
Решение.
Рассмотрим функцию 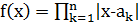 в точках
в точках 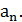
Найдем односторонние пределы 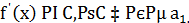
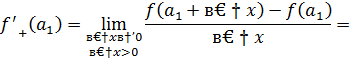
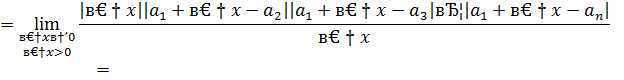
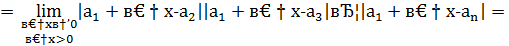
= 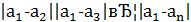
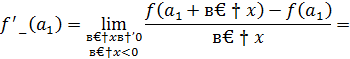
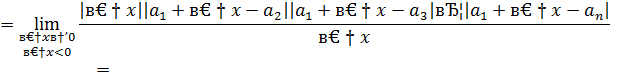
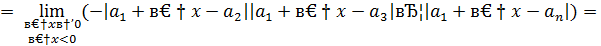
= 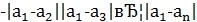
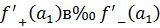
Односторонние пределы не равны 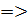 функция
функция 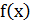 не имеет производной в точке
не имеет производной в точке 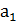 . Аналогично, функция не имеет производных в остальных точках
. Аналогично, функция не имеет производных в остальных точках 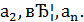
Упражнение 5 ([4], №125)
Показать, что функция 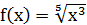 не имеет производной в точке
не имеет производной в точке 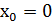 .
.
Решение
Возьмем приращение 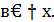 Дадим точке
Дадим точке 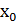 приращение
приращение 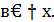 Получим
Получим 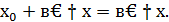
Найдем значение функции в точках 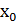 и
и 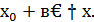
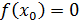
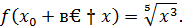
Найдем приращение функции в точке 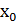
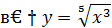
Составим отношение приращения функции в точке к приращению аргумента
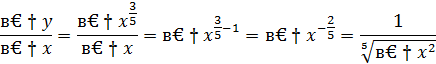
Перейдем к пределу
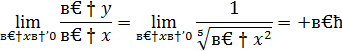
Вывод: не имеет конечной производной в точке 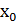 .
.
Упражнение 6 ([4], №128)
Показать, что функция 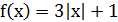 не имеет производной в точке
не имеет производной в точке 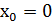 .
.
Решение
Возьмем приращение 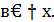 Дадим точке
Дадим точке 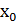 приращение
приращение 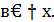 Получим
Получим 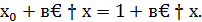
Найдем значение функции в точках 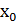 и
и 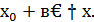
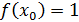
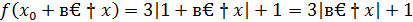
Найдем приращение функции в точке 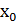
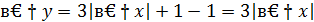
Составим отношение приращения функции в точке к приращению аргумента
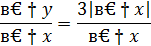
Перейдем к пределу
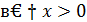
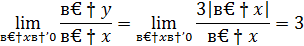
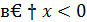
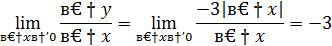
Вывод: не имеет конечной производной в точке 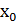 .
.
Упражнение 7 ([4], №131)
Исследовать функцию на непрерывность
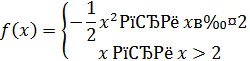
Решение.
На 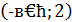
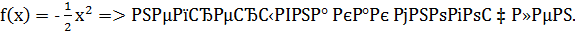
На 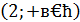
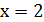 – точка подозрительная на разрыв
– точка подозрительная на разрыв
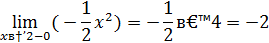
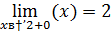
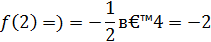
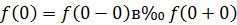
Так как левый предел равен значению функции в точке, то функция непрерывна 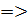 в точке
в точке 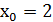 существует разрыв Iрода.
существует разрыв Iрода.
Заключение
|
из
5.00
|
Обсуждение в статье: Пример непрерывной функции без производной |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

