Определение скоростей точек и звеньев механизма

2020-03-19

191

Обсуждений (0)

0.00 из 5.00 0 оценок

123

Определим скорости точек механизма при нахождении кривошипа в каждом из двенадцати положений.

Опишем, как определяется скорость точек механизма при движении кривошипа из первого положения во второе.

Определяем скорость точки A₁. Точка A₁ совершает вращательное движение, линия действия скорости перпендикулярна звену ОА₁, вектор скорости направлен в сторону вращения звена ОА₁. Линейную скорость точки A₁ определяют по формуле (2).

, (2)

где V_A - скорость точки А₁, м/с;

ω - угловая скорость звена ОА₁, с^-1;

|ОА₁| - длина звена ОА₁, м.

, (3)

где ω - угловая скорость звена ОА₁, с^-1;

n - частота вращения звена ОА₁, об/мин.

с^-1

м/с

Выбираем на свободном поле чертежа точку и обозначим ее P_V. P_V - полюс - точка, где все скорости равны нулю. Строим в масштабе вектор скорости точки A₁ с началом в точке P_V.

Определяем скорость точки A₃. Точка A₃ совершает вращательное движение, и ее линейная скорость описывается системой уравнений 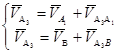(4).

; (4)

Строим линию параллельную к звену 4 проходящую через конец вектора скорости точки A₁, так как шатун совершает поступательное движение вдоль кулисы. После этого строим линию перпендикулярную звену A₃B и проходящую через полюс, так как звено A₃B совершает вращательное движение относительно точки B, то есть точка B является полюсом. Соединяем полюс с точкой пересечения параллельной линии и перпендикуляра. Получим направление и значение скорости точки A₃.

Так как точки A₃ и C принадлежат одному звену ВС, то их угловые скорости равны. Следовательно, можно найти величину вектора скорости точки C путем составления пропорции 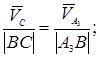(5).

(5)

Строим вектор скорости точки C, который находится на прямой, перпендикулярной звену A₃B и проходящей через полюс.

Определяем скорость точки D. Точка D совершает поступательное движение, и ее линейная скорость описывается системой уравнений (6.)

; (6)

Строим прямую перпендикулярно звену СD_, проходящую через конец вектора скорости точки С, так как точка D совершает вращательное движение относительно точки C. После этого строим линию параллельную траектории точки D и проходящую через полюс. Точку пересечения, перпендикуляра к звену CD и параллельной линии траектории точки D, обозначим "d". Соединив точку d с полюсом, получим значение скорости и направление движения выходного звена.

Так как точки S₄ и C принадлежат одному звену ВС, то их угловые скорости равны. Следовательно, можно найти величину вектора скорости точки S₄ путем составления пропорции (7).

; (7)

Определив положение точки S₄, соединим полюс с этой точкой, умножим на масштаб и получим значение скорости точки S₄.

Скорость точки S₂ равна скорости точки D, так как они совпадают.

Скорость точки S₅ равна скорости точки A₁, так как они совпадают.

Остальные 11 положений строим аналогично.

Результаты занесены в таблицу.

Таблица 3 - Линейные скорости точек механизма

Пол.	V_a	V_a'	V_c	V_d	S₂	S₄	S₅
1	-0,67824	-0,1282	-0,2638	-0,25	-0,25	-0,1346	-0,67824
2	0,67824	0,2145	0,3693	0,351	0,351	0,1924	0,67824
3	0,67824	0,4703	0,710	0,694	0,694	0,3623	0,67824
4	0,67824	0,6260	0,8743	0,870	0,870	0,446	0,67824
5	0,67824	0,6782	0,9220	0,9220	0,9220	0,4710	0,67824
6	0,67824	0,6260	0,8743	0,860	0,860	0,445	0,67824
7	0,67824	0,4703	0,710	0,684	0,684	0,3623	0,67824
8	0,67824	0,2145	0,3693	0,351	0,351	0,1924	0,67824
9	-0,67824	-0,1282	-0,2638	-0,25	-0,25	-0,1346	-0,67824
10	-0,67824	-0,4945	-1,23	-1,20	-1,20	-0,6267	-0,67824
11	-0,67824	-0,678	-1,84	-1,84	-1,84	-0,942	-0,67824
12	-0,67824	-0,4945	-1,23	-1,20	-1,20	-0,6267	-0,67824

2020-03-19

191

Обсуждений (0)

0.00 из 5.00 0 оценок

123

Обсуждение в статье: Определение скоростей точек и звеньев механизма

Обсуждений еще не было, будьте первым... ↓↓↓