 |
Главная |
Определение ускорений точек и звеньев механизма
|
из
5.00
|
Определим ускорения точек механизма при нахождении кривошипа в каждом из двенадцати положений.
Опишем, как определяется ускорение точек механизма при движении кривошипа из первого положения во второе.
Определяем ускорение точки А1. Точка A1 совершает вращательное движение с постоянной скоростью. Ее ускорение описывается формулой (8).
 , (8)
, (8)
где 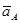 - полное ускорение точки A, м/с2;
- полное ускорение точки A, м/с2;
 - касательное ускорение точки A, м/с2;
- касательное ускорение точки A, м/с2;
 - нормальное ускорение точки A, м/с2.
- нормальное ускорение точки A, м/с2.
Так как скорость вращения постоянна, то касательное ускорение точки A1 равно нулю, следовательно полное ускорение точки A1 равно только нормальному ускорению. Нормальное ускорение точки А1 определяется по формуле (9).
 , (9)
, (9)
где 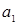 - скорость точки А1, м/с;
- скорость точки А1, м/с;
ω1 - угловая скорость звена ОА1, с-1;
|ОА1| - длина звена ОА1, м.
Угловая скорость ω1 звена ОА1 находится по формуле 3.
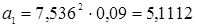 м/с2
м/с2
Выбираем на свободном поле чертежа точку и обозначим ее Pа. Pа - полюс - точка, где все ускорения равны нулю. Строим в масштабе вектор ускорения точки A1 с началом в точке Pа. Этот вектор будет направлен вдоль звена ОА.
Определяем ускорение точки A3. Точка A3 совершает вращательное движение, ускорение описывается системой уравнений (10).
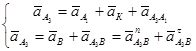 , (10)
, (10)
где 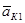 - ускорение Кориолиса, определяющееся по формуле (11);
- ускорение Кориолиса, определяющееся по формуле (11);
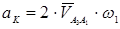 ; (11)
; (11)
Построим в масштабе вектор ускорение Кориолиса. Он проводится из конца вектора ускорения точки А1 и направлен вдоль прямой повернутой на угол 90° относительно скорости  в сторону вращения кулисы. Через конец вектора
в сторону вращения кулисы. Через конец вектора  проводим линию, параллельную кулисе, это линия действия ускорения
проводим линию, параллельную кулисе, это линия действия ускорения  . Ускорение точки В равно нулю. Из полюса в масштабе строим вектор нормального ускорения точки A3. Этот вектор будет направлен вдоль звена A3B от точки A3 к B. Длина этого вектора определяется по формуле (12).
. Ускорение точки В равно нулю. Из полюса в масштабе строим вектор нормального ускорения точки A3. Этот вектор будет направлен вдоль звена A3B от точки A3 к B. Длина этого вектора определяется по формуле (12).
 , (12)
, (12)
где 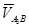 берется из плана скоростей.
берется из плана скоростей.
Через конец вектора 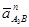 проводим прямую, перпендикулярную отрезку A3B. Эта прямая является линией действия ускорения
проводим прямую, перпендикулярную отрезку A3B. Эта прямая является линией действия ускорения  . Точку пересечения линий действия ускорений
. Точку пересечения линий действия ускорений  и
и  обозначим "а3". Соединив полюс с точкой а3, получим значение и направление ускорения точки А3.
обозначим "а3". Соединив полюс с точкой а3, получим значение и направление ускорения точки А3.
Строим вектор ускорения точки C, который совпадает по направлению с вектором ускорения точки А3, так как точки A3 и C принадлежат одному звену ВС. Величину вектора ускорения точки C можно найти путем составления пропорции (13).
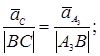 (13)
(13)
Ускорение выходного звена описывается системой уравнений (14).
 , (14)
, (14)
Через полюс проводим прямую, параллельную траектории движения точки D, которая является линией действия ускорения  .
.
Из конца вектора  откладываем вектор
откладываем вектор 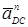 , который параллелен DC и направлен от D к C, длина этого вектора определяется по формуле (15).
, который параллелен DC и направлен от D к C, длина этого вектора определяется по формуле (15).
 ; (15)
; (15)
Через конец вектора 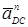 проводим прямую, перпендикулярную отрезку DC, до пересечения с линией действия ускорения
проводим прямую, перпендикулярную отрезку DC, до пересечения с линией действия ускорения 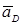 . Эта прямая является линией действия ускорения
. Эта прямая является линией действия ускорения  . Получили точку пересечения прямой параллельной траектории движения точки D и
. Получили точку пересечения прямой параллельной траектории движения точки D и  , обозначив ее "d". Соединив полюс с этой точкой, получим значение и направление ускорения точки D.
, обозначив ее "d". Соединив полюс с этой точкой, получим значение и направление ускорения точки D.
Ускорения точек, S2, S4, S5, определяются аналогично скоростям соответствующих точек.
Остальные 11 положений строим аналогично.
Для того чтобы построить график зависимости ускорения выходного звена от положения кривошипа составим таблицу 4.
Таблица 4 - Ускорения точек механизма
| Пол. | аА1 | аА3 | аС | aD | S2 | S4 | S5 |
| 1 | 5,1112 | 4,3025 | 8,853 | 8,313 | 8,313 | 4,517 | 5,1112 |
| 2 | 5,1112 | 3,883 | 6,685 | 6,384 | 6,384 | 3,411 | 5,1112 |
| 3 | 5,1112 | 2,367 | 3,574 | 3,706 | 3,706 | 1,824 | 5,1112 |
| 4 | 5,1112 | 1,523 | 2,127 | 1,6342 | 1,6342 | 1,085 | 5,1112 |
| 5 | 5,1112 | 1,277 | 1,738 | 0,1735 | 0,1735 | 0,887 | 5,1112 |
| 6 | -5,1112 | -1,523 | -2,127 | -1,6342 | -1,6342 | -1,085 | -5,1112 |
| 7 | -5,1112 | -2,367 | -3,574 | -3,706 | -3,706 | -1,824 | -5,1112 |
| 8 | -5,1112 | -3,883 | -6,6854 | -6,470 | -6,470 | -3,411 | -5,1112 |
| 9 | -5,1112 | -4,3025 | -8,853 | -8,510 | -8,510 | -4,517 | -5,1112 |
| 10 | -5,1112 | -1,7046 | -4,2342 | -4,0 | -4,0 | -2,16 | -5,1112 |
| 11 | 5,1112 | 2,555 | 6,950 | 0,695 | 0,695 | 3,549 | 5,1112 |
| 12 | 5,1112 | 1,7046 | 4,2342 | 3,85 | 3,85 | 2,16 | 5,1112 |
Заключение
В курсовой работе произведено структурное и кинематическое исследования механизма поперечно-строгательного станка.
В структурном исследовании определено количество и виды звеньев и кинематических пар, также определена подвижность механизма и поведена структурная классификация механизма по Асуру.
В кинематическом исследовании описано построение плана положений, определение скоростей и ускорений точек механизма.
В рабочем чертеже разработаны план положений, планы скоростей и планы ускорений всех звеньев механизма при разных положениях кривошипа. Начерчены графики, в которых определены зависимости перемещений, скоростей и ускорений выходного звена от разных положений кривошипа.
|
из
5.00
|
Обсуждение в статье: Определение ускорений точек и звеньев механизма |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

