 |
Главная |
Необходимое и достаточное условие существования экстремума функций одной переменной
|
из
5.00
|
Классические методы оптимизации
Выполнила:
студентка 3 курса, 306 группы
Черпакова Надежда Анатольевна
Научный руководитель:
к. ф.-м. н., доцент
Холодков А.В.
Барнаул - 2013
Оглавление
Введение
. Классические методы безусловной оптимизации
Необходимое и достаточное условие существования экстремума функций одной переменной
Необходимое и достаточное условие существования экстремума функций нескольких переменных
. Условная оптимизация
Правило множителей Лагранжа. Необходимые условия оптимальности
Достаточные условия оптимальности
3. Практическая часть
3.1 Безусловная оптимизация
3.2 Метод Лагранжа
Заключение
Список литературы
Введение
Методы исследования функций классического анализа представляют собой наиболее известные методы решения несложных оптимальных задач, с которыми известны из курса математического анализа. Обычной областью использования данных методов являются задачи с известным аналитическим выражением критерия оптимальности, что позволяет найти не очень сложное, также аналитическое выражение для производных. Полученные приравниванием нулю производных уравнения, определяющие экстремальные решения оптимальной задачи, крайне редко удается решить аналитическим путем, поэтому, как, правило, применяют вычислительные машины. При этом надо решить систему конечных уравнений, чаще всего нелинейных, для чего приходится использовать численные методы, аналогичные методам нелинейного программирования.
Методы исследования при наличии ограничений на область изменения независимых переменных можно использовать только для отыскания экстремальных значений внутри указанной области. В особенности это относится к задачам с большим числом независимых переменных (практически больше двух), в которых анализ значений критерия оптимальности на границе допустимой области изменения переменных становится весьма сложным.
Цель данной курсовой работы - изучить классические методы оптимизации и разобрать примеры с применением изученных методов.
Задачи:
- описать основную теорию;
- рассмотреть решения некоторых примеров.
Классические методы безусловной оптимизации.
Классический подход к задаче определения локальных и глобальных минимумов состоит в использовании методов математического анализа для поиска уравнений, которым должны удовлетворять эти точки, и для решения этих уравнений [2].
Необходимое и достаточное условие существования экстремума функций одной переменной
Определение 1.1. Функция f(x) одной переменной имеет локальный минимум в точке x, если существует  , такая, что
, такая, что  для всех
для всех  , то есть если существует некоторая окрестность точки
, то есть если существует некоторая окрестность точки  , в которой значение функции в любой ее точке больше, чем
, в которой значение функции в любой ее точке больше, чем 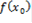 [1].
[1].
Определение 1.2. Функция  имеет глобальный минимум в точке
имеет глобальный минимум в точке 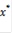 , если
, если  для всех x из области определения f(x) [1].
для всех x из области определения f(x) [1].
Из рисунка 1 видно, что в точках  и
и 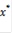 касательная к графику функции будет параллельна оси OX, а это означает, что производная функции
касательная к графику функции будет параллельна оси OX, а это означает, что производная функции  в этих точках будет равна нулю. Следовательно,
в этих точках будет равна нулю. Следовательно,  и
и  будут решениями уравнения
будут решениями уравнения  .
.
Однако это же справедливо и для точки максимума  , и для точки перегиба
, и для точки перегиба  . Таким образом, найденное уравнение является необходимым условием минимума, но не является достаточным.
. Таким образом, найденное уравнение является необходимым условием минимума, но не является достаточным.
В точках 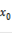 и
и  производная
производная  меняет знак с отрицательного на положительный, в
меняет знак с отрицательного на положительный, в  - с положительного на отрицательный, в точке
- с положительного на отрицательный, в точке  производная знак не меняет. Следовательно, в точке минимума производная является возрастающей функцией. Степень же возрастания измеряется второй производной, то есть в нашем случае
производная знак не меняет. Следовательно, в точке минимума производная является возрастающей функцией. Степень же возрастания измеряется второй производной, то есть в нашем случае  ,
,  ,
, 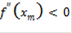 . Однако если
. Однако если 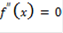 , то ситуация остается неопределенной[2].
, то ситуация остается неопределенной[2].
Надежное основание для полученных результатов дает разложение функции в ряд Тейлора в окрестности точки 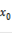 (
(  ,
, 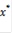 ).
).
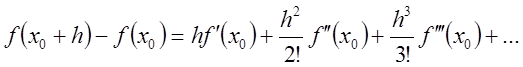
Если 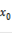 - точка минимума, то
- точка минимума, то  для любого достаточно малого h.
для любого достаточно малого h.
Если  , то отрицательное h сделает отрицательной разность
, то отрицательное h сделает отрицательной разность  , что невозможно в точке минимума. Если
, что невозможно в точке минимума. Если 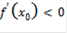 , то произойдет то же самое, если выбрать положительное h. Следовательно,
, то произойдет то же самое, если выбрать положительное h. Следовательно,  - это необходимое условие существования минимума в точке
- это необходимое условие существования минимума в точке  .
.
Так как  всегда, то при
всегда, то при  и
и  всегда выполняется
всегда выполняется  , то есть
, то есть 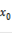 - точка минимума, а при
- точка минимума, а при  ,
,  (h - любое) и
(h - любое) и 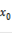 - точка максимума. Следовательно, это достаточные условия.
- точка максимума. Следовательно, это достаточные условия.
Если же  , то рассуждения, аналогичные проведенным для первой производной, можно повторить для
, то рассуждения, аналогичные проведенным для первой производной, можно повторить для 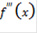 и так далее [2].
и так далее [2].
Это позволяет сформулировать следующее правило:
|
из
5.00
|
Обсуждение в статье: Необходимое и достаточное условие существования экстремума функций одной переменной |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

