Базовые трехмерные объекты

Сфера

Сфера является одной из наиболее просто аналитически задаваемых объектов. В программе для ее определения хранятся координаты ее центра и длина радиуса.

Задача поиска пересечения луча со сферой достаточно проста и позволяет определить факт отсутствия пересечения на ранних этапах вычисления, что приводит к уменьшению времени выполнения программы и позволяет применять сферу в качестве объемной оболочки объекта, вычисление пересечения луча с которым требует больших вычислительных затрат.

На рис. 2.10 изображена сфера и два пересекающих ее луча, начало одного из которых лежит внутри сферы, а другого – снаружи. Задачу можно рассматривать как плоскую – нахождение пересечения луча с окружностью, в силу того, что через прямую, вдоль которой распространяется луч, и центр окружности, всегда можно провести плоскость, а линия пересечения сферы с плоскостью, проходящей через ее центр, является окружностью с радиусом, равным радиусу самой сферы.

Нахождение точки пересечения луча со сферой

 

Рис. 2.10

 

Рассмотрим первый случай, когда начало луча лежит вне сферы – в точке , направление луча определено единичным вектором . Чтобы найти точку пересечения, достаточно определить расстояние до нее от начала луча в направлении хода луча, то есть длину отрезка . Зная координаты центра окружности , можно определить вектор , а затем и скалярное произведение , численно равное длине отрезка . Если скалярное произведение получилось отрицательным или равным нулю – луч заведомо не пересекает сферу и дальнейшие проверки не производятся.

Иначе находим расстояние от центра сферы до луча – длину отрезка 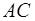. В треугольнике 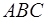, зная длины  и 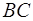, можно найти длину отрезка . Здесь производится следующая проверка: если 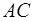 (являющийся расстоянием от центра сферы до луча) больше радиуса сферы, луч сферу не пересекает.

Из треугольника 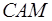 можно аналогичным образом получить длину отрезка , вычитая который из известного уже отрезка , получаем искомое расстояние. Если оно меньше или равно нулю, значит, начало луча лежит на поверхности сферы или же внутри нее (случай луча с началом в 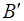), тогда искомое расстояние вычисляется путем сложения длин отрезков  и .

Нормаль к поверхности в любой точке сферы вычисляется тривиальным образом как вектор, соединяющий центр сферы с точкой на поверхности.

Треугольник

Треугольник является примитивом, посредством которого могут быть составлены практически любые многогранные тела. Он задается точкой  – одной из вершин треугольника – и двумя векторам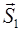и  и 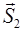, определяющими ориентацию и длины его сторон (см. рис. 2.11).

 

Треугольник

Рис.2.11 Пересечение луча с плоскостью

Рис. 2.12

 

Поиск пересечения луча с треугольником состоит из двух этапов: поиск пересечения луча с плоскостью треугольника и определение нахождения точки внутри него.

Первый этап, изображенный на рис. 2.12, достаточно прост; производится проверка, пересекает ли луч плоскость, путем сравнения с нулем скалярного произведения 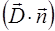. Если оно больше или равно нулю, пересечение отсутствует, и дальнейшие действия можно не выполнять. Вектор, соединяющий произвольную точку плоскости (в данном случае это угол треугольника) с началом луча, проецируется на нормаль и делится на косинус угла между направлением луча и нормалью.

Таким образом, расстояние от источника луча до точки пересечения равно:

 

                                                                     (2.11)

 

Второй этап, заключающийся в определении принадлежности точки треугольнику, существенно сложнее и потребует дополнительных рассуждений.

Локальная система координат

Рис. 2.12 Введем локальную систему координат , в которой оси направлены вдоль сторон, причем в пределах треугольника координаты меняются на величину в диапазоне от 0 до 1 и лежат в заштрихованной области (см. рис. 2.12)

 

Для этого введем дополнительные переменные:

 

                                                                               (2.12)

                                                                             (2.13)

                                                                              (2.14)

                                                                     (2.15)

                                                                      (2.16)

 

На основании формул (2.13) и (2.14) введем значение координат в точке плоскости треугольника следующим образом:

 

                                                                             (2.17)

где  - радиус-вектор точки  на плоскости, содержащей треугольник. Тогда координаты в исходной точке  будут равны:

 

                                                                           (2.18)

 

где 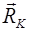 - радиус-вектор точки .

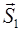В силу того, что радиус-вектор точки внутри треугольника может быть представлен в виде суммы радиус-вектора точки  и линейной комбинации векторов  и 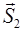, можем записать разницу координат между произвольной точкой  внутри треугольника и исходной точкой :

 

 

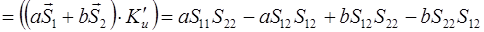
Окончательно:

 

                                                           (2.19)

 

Аналогичным образом можно получить:

 

                                                            (2.20)

 

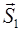Так как  и  являются множителями в линейной комбинации векторов  и 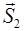, дающей в результате вектор, конец которого лежит внутри треугольника, если начало привести в точку , то  и 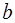 меняются в пределах от 0 до 1. Тогда, поделив полученные в формулах (2.19) и (2.20) разницы на величину:

 

                                                                     (2.21)

 

мы получим требуемый результат – локальные координаты в пределах треугольника меняются не более чем на единицу.

Окончательно имеем формулы для относительных локальных координат:

 

                                                      (2.22)

 

Подставляя найденные на первом этапе координаты точки на плоскости в эти выражения и проверив полученные результаты на нахождение в интервале 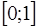 и условию , можно сказать, лежит ли точка внутри треугольника, или нет.

Нормаль к треугольнику в любой его точке определяется как векторное произведение векторов, задающих его стороны.

Текстура и фактура

Общие сведения

В данной программе предусмотрено наложение на трехмерные объекты текстур и имитация шероховатостей поверхностей. Для этого предусмотрена загрузка битовых карт формата *.bmp из внешних файлов.

Основное отличие фактуры от текстуры – фактура вызывает изменение направления нормали для данной поверхности