 |
Главная |
Применение обобщенного суммирования к умножению рядов
|
из
5.00
|
Остановимся на применении обобщенных методов суммирования в вопросе об умножении рядов по правилу Коши. Пусть, кроме ряда (А), дан ещё ряд
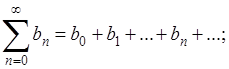 (В)
(В)
тогда ряд
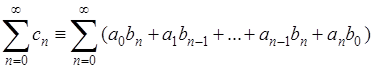 (С)
(С)
и называется произведением рядов (А) и (В) в форме Коши. Если данные ряды сходятся и имеют обыкновенные суммы А и В, то ряд (С) все же может оказаться расходящимся.
Однако во всех случаях ряд (С) суммируем по методу Пуассона-Абеля и именно к сумме АВ.
Действительно, для 0< x<1 ряд (1) равно как и ряд
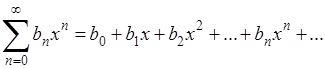
оба абсолютно сходятся; обозначим их суммы, соответственно, через 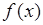 и
и 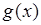 . Произведение этих рядов, то есть ряд
. Произведение этих рядов, то есть ряд
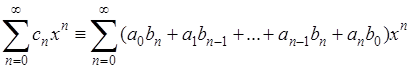 ,
,
По классической теореме Коши также сходится и имеет суммой произведение 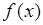 *
* 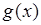 . Эта сумма при
. Эта сумма при 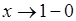 стремится к АВ, ибо как мы видели, по отдельности
стремится к АВ, ибо как мы видели, по отдельности

Итак, “обобщенной (в смысле Пуассона-Абеля) суммой” ряда (С) действительно будет АВ, что и требовалось доказать.
Отсюда как следствие получается теорема Абеля об умножении рядов. Равным образом из самого доказательства ясно, что то же заключение остается в силе, если ряды (А) и (В) - вместо того, чтобы сходиться в собственном смысле - лишь суммируемы по методу Пуассона-Абеля к суммам А и В.
В таком случае, учитывая теорему Фробениуса, можно сделать и следующее утверждение: если (А), (В) и (С) суммируемы в смысле Чезаро и имеют, соответственно, “обобщенные суммы" А, В и С, то необходимо С=АВ.
В качестве примера рассмотрим возведение в квадрат ряда
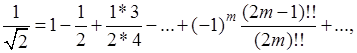
который получается из биномиального разложения
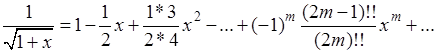
при х=1. умножая указанный числовой ряд на самого себя, придем к хорошо знакомому нам ряду
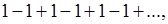
“обобщенная сумма" которого есть 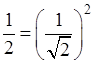 .
.
Далее, “возведем в квадрат" и этот расходящийся ряд. Мы получим ряд
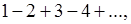 “обобщенная сумма" которого в смысле Пуассона-Абеля есть
“обобщенная сумма" которого в смысле Пуассона-Абеля есть 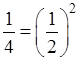 .
.
Глава 4. Другие методы обобщенного суммирования
Методы Г.Ф. Вороного
Пусть мы имеем положительную числовую последовательность 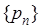 и
и
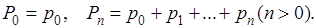
Из частичных сумм 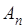 ряда (А) составим выражения
ряда (А) составим выражения
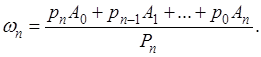
Если 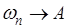 при
при 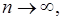 то А называется “обобщенной суммой” ряда (А) в смысле Вороного - при заданном выборе последовательности
то А называется “обобщенной суммой” ряда (А) в смысле Вороного - при заданном выборе последовательности 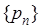 .
.
Теорема.
Для регулярности метода Вороного необходимо и достаточно условие.
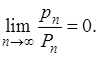
Доказательство. Необходимость.
Допустим сначала регулярность рассматриваемого метода: пусть из 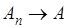 всегда следует и
всегда следует и 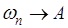 . Если, в частности, взять ряд
. Если, в частности, взять ряд 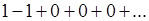 для которого
для которого 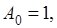 а прочие
а прочие 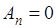 (так что и
(так что и 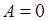 ), то необходимо
), то необходимо
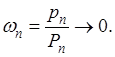
Достаточность. Предположим теперь условие теоремы выполненным и докажем, что из 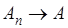 вытекает и
вытекает и 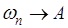 .
.
Обратимся к теореме Теплица и заменим там 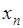 на
на 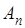 и
и 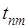 на
на 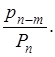 Условие (а) этой теоремы удовлетворено, ибо
Условие (а) этой теоремы удовлетворено, ибо
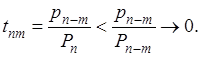
Выполнение условий (б) и (в) очевидно, так как
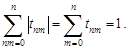
Следовательно, как и требовалось доказать, 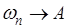 .
.
|
из
5.00
|
Обсуждение в статье: Применение обобщенного суммирования к умножению рядов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

