 |
Главная |
Глава 2. Метод степенных рядов
|
из
5.00
|
Введение
Как мы уже знаем математический анализ, занимается проблемами изучения множества объектов, таких как: числа, переменные, функции, последовательности, ряды и др. При изучении свойств того или иного объекта могут возникать пробелы или “пустоты". Это возникает тогда, когда наука не может объяснить: “Почему происходит так, а не иначе? ”. Такой казус существовал некоторое время и при изучении рядов, а точнее при изучении расходящихся рядов.
При изучении рядов заданному числовому ряду
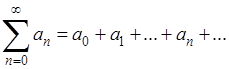 (А)
(А)
в качестве его суммы мы приписывали предел её частичной суммы 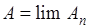 , в предположении, что этот предел существует и конечен. “Колеблющийся" расходящийся ряд оказывался лишенным суммы и подобные ряды, как правило, из рассмотрения исключали. Естественно возникает вопрос о возможности суммирования расходящихся рядов в некоем новом смысле, конечно отличном от обычного. Этот вопрос возник ещё до второй половины XIX века. Некоторые методы такого суммирования оказались довольно-таки плодотворными.
, в предположении, что этот предел существует и конечен. “Колеблющийся" расходящийся ряд оказывался лишенным суммы и подобные ряды, как правило, из рассмотрения исключали. Естественно возникает вопрос о возможности суммирования расходящихся рядов в некоем новом смысле, конечно отличном от обычного. Этот вопрос возник ещё до второй половины XIX века. Некоторые методы такого суммирования оказались довольно-таки плодотворными.
В данной своей работе я хочу рассмотреть эти методы, обратить внимание на то, где и какой метод наиболее применим, изучить связь между этими методами. Моя работа состоит из 4 глав, первая из которых содержит основные термины и определения необходимые для работы. Последующие главы рассматривают непосредственно сами методы суммирования. Вторая и третья главы посвящены двум основным методам суммирования: метод степенных рядов и метод средних арифметических, а третья содержит сведения о других существующих, но реже применяемых методах. Каждая из четырех глав содержит примеры суммирования рядов по данному конкретному методу.
Глава 1. Основные понятия теории рядов
Определения и термины
Как мы упомянули вначале цель нашего исследования - расходящиеся ряды. А что же такое, вообще, ряд?
Пусть задана некоторая бесконечная последовательность чисел
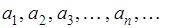 (1)
(1)
Составленный из этих чисел символ
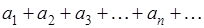 (2)
(2)
называется бесконечным рядом, а сами числа (1) - членами ряда. Вместо (2), пользуясь знаком суммы, часто пишут так:
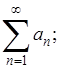 (2а)
(2а)
Станем последовательно складывать члены ряда, составляя (в бесконечном количестве) суммы;
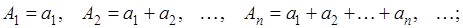 (3)
(3)
их называют частичными суммами ряда.
Конечный или бесконечный предел А частичной суммы 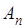 ряда (2) при
ряда (2) при 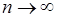 :
: 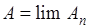
называют суммой ряда и пишут
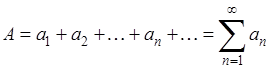 ,
,
Придавая тем самым символу (2) или (2а) числовой смысл. Если ряд имеет конечную сумму, его называют сходящимся, в противном же случае (т. е если сумма равна 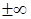 , либо же суммы вовсе нет) - расходящимся.
, либо же суммы вовсе нет) - расходящимся.
Примеры.1) простейшим примером бесконечного ряда является уже знакомая геометрическая прогрессия:
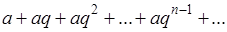
Его частичная сума будет (если 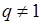 )
)
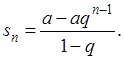
Если знаменатель прогрессии, q, по абсолютной величине меньше единицы, то 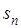 имеет конечный предел
имеет конечный предел
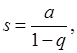
то есть наш ряд сходится, и 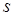 будет его суммой.
будет его суммой.
При 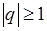 та же прогрессия дает пример расходящегося ряда. Если
та же прогрессия дает пример расходящегося ряда. Если 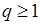 , то его суммой будет бесконечность (определенного знака), в прочих случаях суммы вовсе нет. Отметим, в частности, любопытный ряд, который получается при a=1 и q= - 1;
, то его суммой будет бесконечность (определенного знака), в прочих случаях суммы вовсе нет. Отметим, в частности, любопытный ряд, который получается при a=1 и q= - 1;
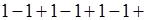 …
… 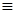 1+ (-1) +1+ (-1) +1+…
1+ (-1) +1+ (-1) +1+…
Его частичные суммы попеременно равны то 1, то 0.
2) Легко установить расходимость ряда
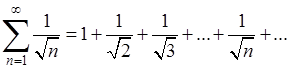
В самом деле, так как члены его убывают, то его n-я частичная сумма

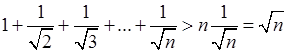
и растет до бесконечности вместе с n.
Истоки проблемы
Различные факты из области математического анализа, как, например, расходимость, произведения двух сходящихся рядов, естественно выдвинули вышеупомянутый вопрос: “О возможности суммирования расходящихся рядов, в некоем новом смысле”.
Нужно сказать, что до создания Коши строгой теории пределов (и связанной с нею теории рядов) расходящиеся ряды нередко встречались в математической практике.
Хотя применение их при доказательствах и оспаривалось, тем не менее иной раз делались попытки придавать им даже числовой смысл.
Вспомним, опять, наш колеблющийся ряд
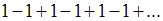
Еще со времен Лейбница в качестве "суммы" приписывалось число 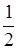 . Эйлер, например, мотивировал это тем, что из разложения
. Эйлер, например, мотивировал это тем, что из разложения
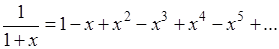
(которое в действительности имеет место лишь для 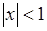 ) при подстановке вместо х единицы как раз и получается
) при подстановке вместо х единицы как раз и получается
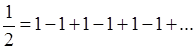
В этом уже содержалось зерно истины, но постановке вопроса не хватало четкости; самый произвол в выборе разложения оставлял открытой возможность, скажем из другого разложения (где п и т - любые, но 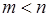 )
)
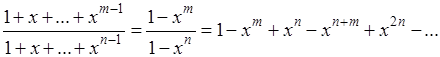
получить одновременно
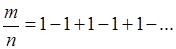
Современный анализ ставит вопрос по-другому. В основу кладется то или иное точно сформулированное определение “обобщенной суммы" ряда, не придуманное только для конкретно интересующего нас числового ряда, но приложимое к целому ряду классов таких рядов. Определение “обобщенной суммы" обычно подчиняется двум требованиям.
Во-первых, если ряду  приписывается “обобщенная сумма" А, а ряду
приписывается “обобщенная сумма" А, а ряду 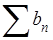 - “обобщенная сумма" В, то ряд
- “обобщенная сумма" В, то ряд 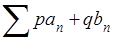 , где p, q - две произвольные постоянные, то должен иметь в качестве “обобщенной суммы" число
, где p, q - две произвольные постоянные, то должен иметь в качестве “обобщенной суммы" число 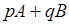 . Метод суммирования, удовлетворяющий этому требованию, называется линейным.
. Метод суммирования, удовлетворяющий этому требованию, называется линейным.
Во-вторых, новое определение должно содержать обычное определение как частный случай. Точнее говоря, ряд, сходящийся в обычном смысле к сумме А, должен иметь “обобщенную сумму", и притом также равную А. Метод суммирования, обладающий этим свойством, называют регулярным. Разумеется, интерес представляют лишь такие регулярные методы, которые позволяют устанавливать “сумму” в более широком классе случаев, нежели обычный метод суммирования: лишь тогда с полным правом можно говорить об “обобщенном суммировании”. Мы переходим к теперь непосредственно к рассмотрению особо важных с точки зрения приложений методов ‘обобщенного суммирования".
Глава 2. Метод степенных рядов
Суть метода
Этот метод, в существенном принадлежит Пуассону, который сделал первую попытку применить его к тригонометрическим рядам. Он состоит в следующем.
По данному числовому ряду (А) строится степенной ряд
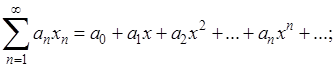 (1)
(1)
Если этот ряд для 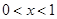 сходится и его сумма
сходится и его сумма 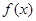 при
при 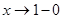 имеет предел А:
имеет предел А:
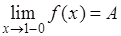 ,
,
то число А и называют “обобщённой (в смысле Пуассона) суммой” данного ряда. Примеры.1) Ряд, рассмотренный Эйлером:
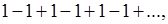
Здесь уже в силу самого определения приводит к степенному ряду, сумма которого 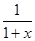 при
при 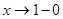 стремится к пределу
стремится к пределу 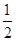 . Значит, число
. Значит, число 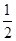 , действительно, является “обобщенной суммой” указанного в точном установленном здесь смысле.
, действительно, является “обобщенной суммой” указанного в точном установленном здесь смысле.
2) Возьмем более общий пример: тригонометрический ряд
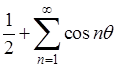 (2)
(2)
является расходящимся при всех значениях 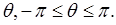
Действительно, если 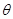 имеет вид
имеет вид 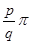 , где
, где 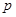 и
и 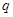 - натуральные числа, то для значений
- натуральные числа, то для значений 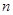 , кратных
, кратных 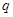 , будет
, будет 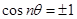 , так что нарушено необходимое условие сходимости ряда. Если же отношение
, так что нарушено необходимое условие сходимости ряда. Если же отношение 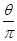 иррационально, то, разлагая его в бесконечную непрерывную дробь и составляя подходящие дроби
иррационально, то, разлагая его в бесконечную непрерывную дробь и составляя подходящие дроби 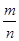 , будем иметь, как известно,
, будем иметь, как известно,
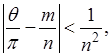 откуда
откуда 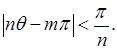
Таким образом, для бесконечного множества значений 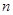
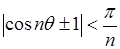 , так что
, так что 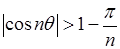 .
.
Это также свидетельствует о нарушении необходимого условия сходимости. Если образовать степенной ряд:
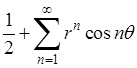
(здесь буква  заменяет прежнюю букву
заменяет прежнюю букву 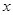 ), то его сумма при значении
), то его сумма при значении 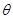 , отличном от 0, будет
, отличном от 0, будет
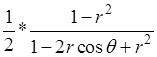 (3)
(3)
и при 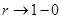 стремится к 0. Таким образом, для
стремится к 0. Таким образом, для 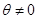 “обобщенной суммой” ряда будет 0. если
“обобщенной суммой” ряда будет 0. если 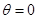 , то ряд (2), очевидно имеет сумму, равную
, то ряд (2), очевидно имеет сумму, равную 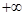 ; впрочем, выражение (3), которое в этом случае сводится к
; впрочем, выражение (3), которое в этом случае сводится к 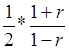 , также имеет пределом
, также имеет пределом 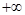 .
.
3) Аналогично ряд
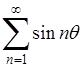
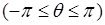 ,
,
который сходится лишь при 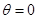 или
или 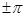 , приводит к степенному ряду
, приводит к степенному ряду
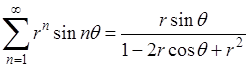 .
.
Так что “обобщенная сумма" на этот раз оказывается равной 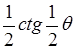 при
при 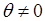 и равной нулю при
и равной нулю при 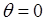 .
.
Непосредственно ясно, что рассматриваемый метод “обобщенного суммирования” является линейным. Что же касается регулярности этого метода, то она устанавливается следующей теоремой принадлежащей Абелю.
2.2 Теорема Абеля [1]
Теорема. Если ряд (А) сходится и имеет сумму А (в обычном смысле), то для 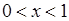 сходится степенной ряд (1), и его сумма стремится к пределу А, когда
сходится степенной ряд (1), и его сумма стремится к пределу А, когда 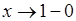 .
.
Доказательство. Начнем с того, что радиус сходимости ряда (1) не меньше 1, так что для 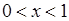 ряд (1), действительно, сходится. Мы имели уже тождество
ряд (1), действительно, сходится. Мы имели уже тождество
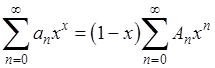
(где 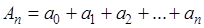 ); вычтем его почленно из тождества
); вычтем его почленно из тождества
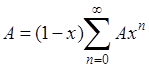 .
.
Полагая 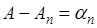 , Придем к тождеству
, Придем к тождеству
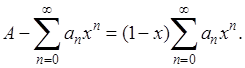 (4)
(4)
Так как 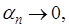 то по произвольно заданному
то по произвольно заданному 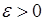 найдется такой номер
найдется такой номер 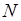 , что
, что 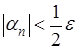 , лишь только
, лишь только 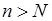 .
.
Разобьем сумму ряда в правой части (4) на две суммы
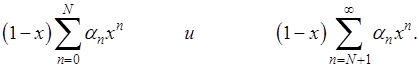
Вторая оценивается сразу и независимо от 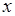 :
:
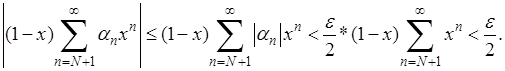
Что же касается первой, то она стремится к 0 при 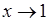 и при достаточной близости
и при достаточной близости 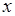 к 1 будет
к 1 будет
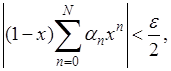
так что окончательно 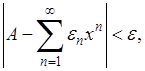 что и доказывает утверждение.
что и доказывает утверждение.
Если ряд (А) суммируем по Пуассону-Абелю к сумме А, то в обычном смысле, как мы видели, он может и не иметь суммы. Иными словами из существования предела
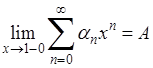 , (5)
, (5)
вообще говоря, не вытекает сходимость ряда (А). Естественно возникает вопрос, какие дополнительные условия надлежит наложить на поведение членов этого ряда, чтобы из (5) можно было заключить о сходимости ряда (  ), т.е. о существовании для него суммы
), т.е. о существовании для него суммы  в обычном смысле. Первая теорема в этом направлении была доказана Таубером.
в обычном смысле. Первая теорема в этом направлении была доказана Таубером.
Теорема Таубера
Теорема. Пусть ряд (1) сходится при 0< x<1, и имеет место предельное равенство (5). Если члены ряда (А) таковы, что
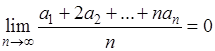 (6)
(6)
то и 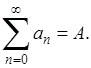
Доказательство. Разобьем доказательство на две части. Сначала
предположим, что 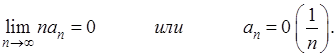 Если положить
Если положить 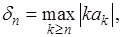 то при
то при 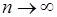 величина
величина 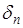 , монотонно убывая, стремится к нулю.
, монотонно убывая, стремится к нулю.
Имеем при любом натуральном N
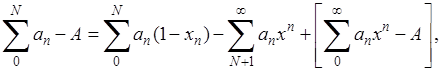
так что:
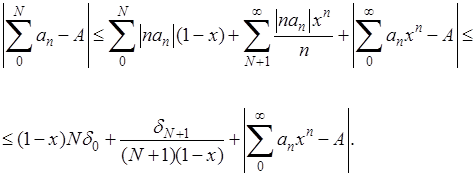
Взяв произвольно малое число 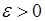 , положим
, положим
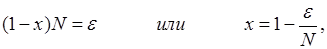
Так что 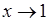 при
при 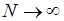 . Пусть теперь
. Пусть теперь 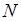 выбрано достаточно большим чтобы: выполнялось неравенство
выбрано достаточно большим чтобы: выполнялось неравенство 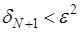 ; соответствующее x было настолько близко к 1, что
; соответствующее x было настолько близко к 1, что
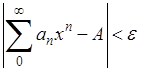 . Тогда
. Тогда 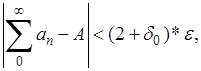
Что и доказывает утверждение теоремы.
К рассмотренному частному случаю теоремы приводится и общий. Положим
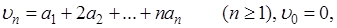 так что
так что
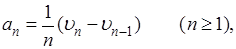 и затем
и затем
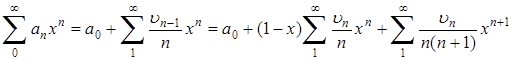 (7)
(7)
Но из предположения теоремы, т.е. из того, что 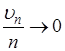 при
при 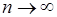 , легко получить, что
, легко получить, что
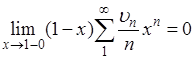 . (8)
. (8)
Для доказательства этого достаточно разбить здесь сумму на две:
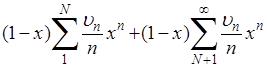
и выбрать N таким, чтобы во второй сумме все множители 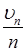 были по абсолютной величине меньшими наперед заданного числа
были по абсолютной величине меньшими наперед заданного числа 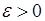 , тогда и вторая сумма по абсолютной величине будет меньше
, тогда и вторая сумма по абсолютной величине будет меньше 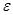 , каково бы ни было х; относительно первой суммы, состоящей из определенного конечного числа слагаемых, того же можно достигнуть за счет приближения х к 1.
, каково бы ни было х; относительно первой суммы, состоящей из определенного конечного числа слагаемых, того же можно достигнуть за счет приближения х к 1.
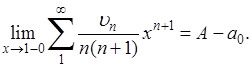
Но здесь уже можно применить доказанный частный случай теоремы, так что и
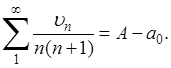 С другой стороны,
С другой стороны,
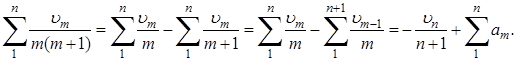
Отсюда, так как первое слагаемое справа стремится к нулю
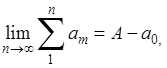
Что и завершает доказательство теоремы.
|
из
5.00
|
Обсуждение в статье: Глава 2. Метод степенных рядов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

