ТЕМА7. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

 

Понятие производной. Геометрический смысл. Правила вычисления производных. Производная сложной функции. Таблица производных. Производные высших порядков. Понятие дифференциала и его геометрический смысл. Применение дифференциала для приближенных вычислений. Инвариантность дифференциала. Формула Тейлора и остаточный член. Формула Тейлора для элементарных функций. применение для приближенного вычисления функций и пределов. содержащих неопределенность. Возрастание и убывание функций. Экстремумы. выпуклость, вогнутость, точки перегиба. асимптоты. Построение графиков.

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

 

 

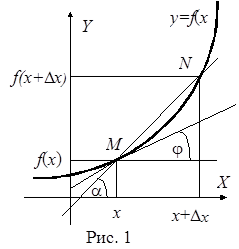
Рассмотрим функцию y=f(x), непрерывную в некоторой окрестности точки x. Пусть Dx  приращение аргумента в точке x. Обозначим через Dy или Df приращение функции, равное f(x+Dx) – f(x). Отметим здесь, что функция непрерывна в точке x, если в этой точке бесконечно малому приращению аргумента Dx соответствует бесконечно малое приращение функции Df.

Отношение Df /Dx, как видно из рисунка 1, равно тангенсу угла a, который составляет секущая MN кривой y = f(x) c положительным направлением горизонтальной оси координат.

Отношение Dy / Dx или, что то же самое (f(x + Dx)  f(x)) / Dx, можно рассматривать при заданном x как функцию аргумента Dx. Эта функция не определена в точке Dx = 0. Однако её предел в этой точке может существовать.

Если существует предел отношения (f(x + Dx) – f(x)) / Dx в точке Dx = 0, то он называется производной функции y = f(x) в точке x и обозначается y¢ или f¢(x):

.

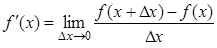Нахождение производной функции y = f(x) называется дифференцированием.

Если для любого числа x из открытого промежутка (a, b) можно вычислить f¢(x), то функция f(x) называется дифференцируемой на промежутке (a, b).

Геометрический смысл производной заключается в том, что производная функции f(x) в точке x равна тангенсу угла наклона касательной к графику функции в этой точке.

Производная  это скорость изменения функции в точке x. Из определения производной следует, что f¢ (x) » Df / Dx, причем точность этого приближенного равенства тем выше, чем меньше Dx. Производная f¢ (x) является приближенным коэффициентом пропорциональности между Df и Dx.

 

Таблица производных элементарных функций.

f(x)		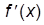f(x)		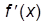f(x)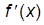
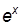
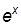
C	0			cosx	-sinx
x	1	lnx	1/x	tgx	1/cos2x
xn	nxn-1	ax	axlna	arcsina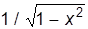
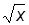
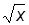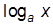
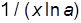
	1/(2 )			arccosa	-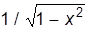
1/x	-1 / x2	sinx	cosx	arctgx	1/(1+x2)

 

Основные свойства производной.

1. Если функция имеет производную в точке, то она непрерывна в этой точке.

2. Если существует f¢ (x) , и С ‑ произвольное число, то функция 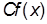 имеет производную: (Cf(x))¢ = Cf¢ (x).

3. Если существуют f¢ (x) и g¢ (x), то функция S(x) = f(x) + g(x) имеет производную: S¢ (x) = f¢ (x) + g¢ (x).

4. Если существуют f¢ (x) и g¢ (x), то функция P(x) = f(x)g(x) имеет производную: P¢ (x) = f¢ (x)g(x) + f(x)g¢ (x).

5. Если существуют f¢ (x) и g¢ (x) и при этом g(x) ¹ 0, то функция D(x) = f(x) / g(x) имеет производную: D¢ (x) = (f¢ (x) g(x)  f(x) g¢ (x)) / g²(x).

Производная сложной функции.

Пусть функция g(x) имеет производную в точке x, а функция f(z) имеет производную в точке z = g(x). Тогда сложная функция F(x) = f(g(x)) имеет в точке x производную F¢ (x) = f¢ (z) g¢ (x).

Назовем функцию b (z) бесконечно малой в точке z = z₀, если .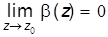

Пусть функции b (z) и g (z) являются бесконечно малыми в точке z = z₀.. Функция b (z) называется бесконечно малой более высокого порядка, чем функция g (z), если .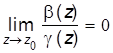

Величины r₁ и r₂ в формулах (2) являются функциями аргумента Dx, бесконечно малыми в точке Dx = 0. Можно показать, что 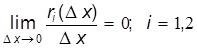. Это означает, что функции r₁(Dx) и r₂(Dx) являются бесконечно малыми функциями более высокого порядка, чем Dx, в точке Dx = 0.

Таким образом приращение функции y = f(x) в точке, в которой существует её производная, может быть представлено в виде

Dy = f¢(x) Dx +b (Dx),

где b (Dx) ‑ бесконечно малая функция более высокого порядка, чем Dx, в точке Dx = 0.

Главная, линейная относительно Dx, часть приращения функции y = f(x), равная f¢ (x) Dx, называется дифференциалом и обозначается dy:

dy = f¢ (x) Dx.

,

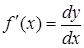то есть производная функции f(x) равна отношению дифференциала функции к дифференциалу аргумента x.

Свойства дифференциала.

1. dC = 0 ( здесь и в следующей формуле C  постоянная );

2. d(Cf(x)) = Cdf(x);

3. Если существуют df(x) и dg(x), то d(f(x) + g(x)) = df(x) + dg(x), d(f(x)g(x)) = g(x)df(x) + f(x)dg(x). Если при этом g(x) ¹0, то  .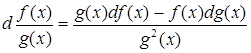

Пусть функция y=f(x) дифференцируема на некотором отрезке [ab]. В таком случае ее производная представляет собой тоже некоторую функцию х. Продифференцировав эту функцию, мы получим так называемую вторую производную (или производную второго порядка) функции f(x). Продолжая эту операцию, можно получить производные третьего, четвертого и более высоких порядков. При этом f`(x) будем называть производной первого порядка.

Производной n-го порядка (или n-й производной) от функции f(x) называется производная (первого порядка) от ее (n-1)-й производной.

Обозначение: у⁽ⁿ⁾=(y^(n-1))΄=f⁽ⁿ⁾(x). Производные 2-го и 3-го порядка обозначаются соответственно y′΄ и y΄′΄.

Свойства производных высших порядков.

Основные свойства производных высших порядков следуют из соответствующих свойств первой производной:

1. (cf(x))⁽ⁿ⁾=c·f⁽ⁿ⁾(x).

2. (f(x)+g(x))⁽ⁿ⁾=f⁽ⁿ⁾(x)+g⁽ⁿ⁾(x).

3. Для y=x^m y⁽ⁿ⁾=n(n-1)…(n-m+1)x^m-n. Если m – натуральное число, то при n>m y⁽ⁿ⁾=0.

4. Можно вывести так называемую формулу Лейбница, позволяющую найти производную n-го порядка от произведения функций f(x)g(x):

 .

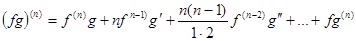Дифференциалы высших порядков.

Дифференциал от дифференциала функции называется ее вторым дифференциалом или дифференциалом второго порядка.

Обозначение: d²y=d(dy).

Дифференциалом n-го порядка называется первый дифференциал от дифференциала (n-1)-го порядка:

dⁿy = d(d^n-1y) = (f^(n-1)(x)d^n-1x)΄ = f⁽ⁿ⁾(x)dⁿx.

Свойства дифференциалов высших порядков.

1. Производную любого порядка можно представить как отношение дифференциалов соответствующего порядка:

.

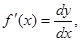
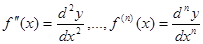2. Дифференциалы высших порядков не обладают свойством инвариантности.

Точки экстремума функции.

Точка х₀ называется точкой максимума (минимума) функции y = =f(x), если f(x) ≤ f(x₀) (f(x) ≥ f(x₀)) для всех х из некоторой δ-окрестности точки х₀ .

Точки максимума и минимума функции называются ее точками экстремума.

Теорема (теорема Ферма). Если функция y = f(x) определена в некоторой окрестности точки х₀, принимает в этой точке наибольшее (наименьшее) в рассматриваемой окрестности значение и имеет в точке х₀ производную, то f′(x₀)=0.

Произведение последовательных натуральных чисел 1∙2∙3∙…∙(n-1)n называется факториалом числа n и обозначается

n! = 1∙2∙3∙…∙(n-1)n .

Дополнительно вводится 0!=1.

 

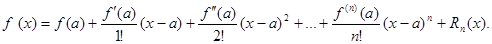
Полученное представление функции называется формулой Тейлора, а R_n(x) называется остаточным членом формулы Тейлора.

Формы остаточного члена в формуле Тейлора.

R_n = o(x-a)ⁿ запись остаточного члена в форме Пеано.

Применение формулы Тейлора для приближенных вычислений.

Заменяя какую-либо функцию, для которой известно разложение по формуле Тейлора, многочленом Тейлора, степень которого выбирается так, чтобы величина остаточного члена не превысила выбранное значение погрешности, можно находить приближенные значения функции с заданной точностью.

Найдем приближенное значение числа е, вычислив значение многочлена Тейлора (21.14) при n=8:

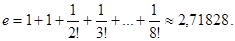 При этом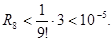

Функция y = f(x) называется возрастающей (убывающей) на [ab], если

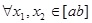 таких, что x₁ < x₂, f(x₁) < f(x₂) ( f(x₁) > f(x₂) ).

Если функция f(x), дифференцируемая на [ab], возрастает на этом отрезке, то 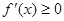 на [ab].

Если f(x) непрерывна на [ab] и дифференцируема на (ab), причем 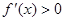 для a < x < b, то эта функция возрастает на отрезке [ab].

Теорема (необходимое условие экстремума). Пусть функция f(x) задана в некоторой окрестности точки х₀. Если х₀ является точкой экстремума функции, то 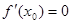 или не существует.

Если функция определена в некоторой окрестности точки х₀ и ее производная в этой точке равна нулю или не существует, точка х₀ называется критической точкой функции.

Достаточные условия экстремума.

Теорема Пусть функция f(x) непрерывна в некоторой окрестности точки х₀, дифференцируема в проколотой окрестности этой точки и с каждой стороны от данной точки f ′(x) сохраняет постоянный знак. Тогда:

1) если f ′(x) > 0 при x < x₀ и f ′(x) < 0 при x > x₀ , точка х₀ является точкой максимума;

2) если f ′(x) < 0 при x < x₀ и f ′(x) > 0 при x > x₀ , точка х₀ является точкой минимума;

3) если f ′(x) не меняет знак в точке х₀ , эта точка не является точкой экстремума.

Наибольшее и наименьшее значения функции, дифференцируемой на отрезке находят по схеме:

1) найти критические точки функции, принадлежащие данному отрезку;

2) вычислить значения функции в точках а и b, а также в найденных критических точках. Наименьшее из полученных чисел будет наименьшим значением функции на данном отрезке, а наибольшее – ее наибольшим значением на нем.

Асимптоты.

Прямая называется асимптотой графика функции y = f(x) , если расстояние от переменой точки этого графика до прямой стремится к нулю при удалении точки в бесконечность.

Рассмотрим три вида асимптот и определим способы их нахождения.

1. Вертикальные асимптоты – прямые, задаваемые уравнениями вида х = а. В этом случае определение асимптоты подтверждается, если хотя бы один из односторонних пределов функции в точке а бесконечен. Пример. Вертикальной асимптотой графика функции y = 1/x является прямая х = 0, то есть ось ординат.

2. Горизонтальные асимптоты – прямые вида у = а. Такие асимптоты имеет график функции, предел которой при 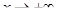 или при  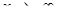конечен, т.е. .

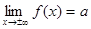3. Наклонные асимптоты – прямые вида y = kx + b. Найдем k и b. Поскольку при 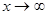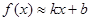, , 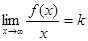если этот предел существует, конечен и не равен нулю. Однако даже при выполнении этих условий наклонная асимптота может не существовать. Для ее существования требуется, чтобы имелся конечный предел при  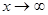разности f(x) – kx. Этот предел будет равен b , так как при .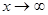

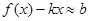Общая схема исследования функции.

1) область определения функции и ее поведение на границах области определения (найти соответствующие односторонние пределы или пределы на бесконечности);

2) четность и периодичность функции;

3) интервалы непрерывности и точки разрыва (указав при этом тип разрыва);

4) нули функции (т.е. значения х , при которых f(x) = 0) и области постоянства знака;

5) интервалы монотонности и экстремумы;

6) интервалы выпуклости и вогнутости и точки перегиба;

7) асимптоты графика функции.

Вопросы для самопроверки.

1.Каков геометрический смысл производной7

2.Каков геометрический смысл дифференциала?

3.Как использовать дифференциал для приближенного вычисления функции?

4.Как найти производную и дифференциал произведения трех функций7

5.Пользуясь определением производной, найдите производную функции у=3х.

6.Как вычисляется производная сложной функции? приведите пример.

7.Что такое вторая производная?

8.Как использовать формулу Тейлора для вычисления приближенных значений функции?

9.Каковы условия возрастания и убывания функции?

10.Сформултруйте необходимое и достаточное условие максимума дифференцируемой функции. В чем различие между необходимым и достаточным условием?

11.Что такое точка перегиба?

12.Какие бывают асимптоты? Приведите примеры.

КОНТРОЛЬНАЯ РАБОТА №1

 

Задача 1.

Даны векторы a и b. Найти вектор c = a + b и скалярное произведение (a ·b),

где a = {1, M + 4, -1, N - 5},b = {-M + 5, -1, 5 – N, 2} .

Задача 2.

Даны матрица А = || а_ij|| размерностью 3´3 и вектор-строка b. Найти произведения А^т × b^т и b ×А;

а_ij = -i – j + M – N – 4, b = {M-5, 1, 4-N}/

Задача 3.

Даны матрицы А = || а_ij|| и В = || b_ij || размерностью 3´3. Проверить, коммутативны ли матрицы А и В, найти определители матриц. Элементы матриц вычисляются по формулам: а_ij = -i – j + M, b_ij = 2i - j + N – 5.

Задача 4.

Решить систему линейных алгебраических уравнений методом Гаусса и с помощью формул Крамера.

х + 2у + 3z = 10,

-2х + у + (N-5)z = N-9,

 x – y + 6z = 7.

Задача 5.

Составить систему из двух уравнений с двумя неизвестными так, чтобы она:

1) имела единственное решение;

2) не имела решений;

3) имела бесконечно много решений.

Найти определители этих систем, учитывая, что каждое из уравнений системы является уравнением прямой линии на плоскости, изобразить эти прямые и пояснить, что означает каждый из трех вариантов с точки зрения взаимного расположения прямых.

Задача 6.

1) Найти расстояние между точками А ( N + 2, -M – 1, M + N) и B ( M,N,M – N) в трехмерном пространстве.

2) Найти точку пересечения прямых у = - (N +1)x +2 и y = (M +1)x – N – M.

3) Найти уравнение прямой, проходящей через точку ( M +1,N +1) и перпендикулярной к прямой у = - 2х –1.

4) какая кривая описывается уравнением (N+1)x² + (M+1)y² =4? Написать каноническое уравнение этой кривой.

Задача 7.

 Найти области определения функций:

а) у = 11 – N – 2x ; б) у = 1 ;

х² + 2 M + 3 x + M + 2

Задача 8.

1. Найти сумму, разность, произведение и частное комплексных чисел z₁ = N + 1 +2i, z₂ = -2 + (M +1)i.

2. Разложить на множители многочлен х² – 2 N + 5 х + N + 6.

 

КОНТРОЛЬНАЯ РАБОТА №2

 

Задача1.

1. Найти пределы:

а) lim [(N + 5)x² + ( M +2) x + ( N + M)];

 ^{x ®2}

б) lim {(10 - N )ln[ e + tg (arcsin x )] + (10 - M)sin [ M + 1) arctg e^x]};

 ^{x ®0}

в) lim (M+3)x^N+5 + (M+1)x^N+2+1

 ^x®¥ (2M+2)x^N+5-1

г) lim N+1+(10-M)x – N+1 -(2M-9)x

 ^x®0 x

д) lim [ x^2(N+1) + (M +5)x^N+1 - x^2(N+1) - (M +1) x ^N+1]

 ^{х ®¥}

е) lim sin [(10 – N)x]

 ^{x ®0} ln[1+(12-M)x]

3. В каких точках непрерывны функции:

а) у = tg (M+3)x ; б) y = 1 ;

x² + 2 Ö N + 3 x + N + 2

Задача №2

Найти производные функций:

1) у = ( M+N+5)x^M+N+2 2) y = ln(x+N)cos(M+2)x-e^(N+1)x tg(M+2)x

3) y = arctg9N+2)x 4) y = sin[ln(3x+N+2)]-arctg[cos(M+3)x]

 ln(2x+M+1)

Задача 3.

Найти вторую производную функции у = е^(N+2)чcos(М+2)х.

Задача 4.

Пользуясь понятием дифференциала, вычислить приближенное значение функции

у = ln[1 + (N+2)x] при х = 0,1

5

Задача 5.

Разложить по формуле Тейлора в окрестности точки х = 0 до членов порядка х² функцию

 у = cos (М+1)х + ln 1 + (N+2)х и найти ее приближенное значение при х = 0,1. Почему

3 4

это приближенное значение более точно соответствует истинному значению функции, чем приближенное значение, полученное с помощью первого дифференциала?

Задача 6.

Пользуясь формулой Тейлора, найти предел lim tg [(N+2)x] ;

 ^x®0 ln [ 1 –(M+3)x]

Задача 7.

Исследовать функции и построить их графики:

а) у = (N+2)x²+x+1 б) y = M+2

x x²+1.