 |
Главная |
Модель фазового кубита
|
из
5.00
|
В работе рассматривалась модель [11] с потенциальным полем 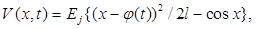 (Рис. 19, сплошная линия) где
(Рис. 19, сплошная линия) где 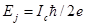 - Джозефсоновская энергия, x - фаза,
- Джозефсоновская энергия, x - фаза,  - нормированная индуктивность перехода, внешнее магнитное поле
- нормированная индуктивность перехода, внешнее магнитное поле  .
.

Рис. 19. Потенциал кубита. Сплошная линия - реальный потенциал. Пунктирная - потенциал с эффективным демпфированием. Вставка - форма импульса f ( t )
В начальный момент времени внешнее поле имеет только постоянную компоненту a 0 такую, что в левой потенциальной яме помещаются два или более энергетических уровня. Таким образом, кубит будет находиться либо на нулевом, либо на первом уровне, что соответствует базисным состояниям |0ñ и |1ñ. Считывание состояния кубита происходит методом быстрого импульсного считывания сигналом амплитуды A и различной формы f ( t ) (Рис. 19). Во время импульса барьер уменьшается так, что в яме остается только нижний уровень, а по окончании импульса в момент 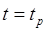 , потенциал возвращается в начальное состояние. Таким образом, если кубит находился на первом энергетическом уровне, то после поданного импульса, кубит будет в правой потенциальной яме. Если же базисное состояние кубита было |0ñ, тогда после считывания волновая функция измениться не должна.
, потенциал возвращается в начальное состояние. Таким образом, если кубит находился на первом энергетическом уровне, то после поданного импульса, кубит будет в правой потенциальной яме. Если же базисное состояние кубита было |0ñ, тогда после считывания волновая функция измениться не должна.
Исследование проведено с помощью компьютерного моделирования [12] уравнения Шредингера для волновой функции Ψ ( x , t ):
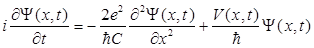 , (31)
, (31)
где  - обратная нормированная емкость контакта. Граничные условия
- обратная нормированная емкость контакта. Граничные условия  задаются для далеко удаленных точек, слева и справа от ямы. Ошибка считывания с кубита N будет определяться суммой вероятностей P 10 (не-туннелирование из состояния |1ñ по окончанию импульса) и P 01 (туннелирование из состояния |0ñ),
задаются для далеко удаленных точек, слева и справа от ямы. Ошибка считывания с кубита N будет определяться суммой вероятностей P 10 (не-туннелирование из состояния |1ñ по окончанию импульса) и P 01 (туннелирование из состояния |0ñ), 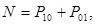 тогда как надежность
тогда как надежность  Для предотвращения ошибки вторичного заселения из-за отсутствия демпфирования в нашей модели [13], введем эффективное демпфирование. Так как нас интересует только туннелирование из левой потенциальной ямы, изменим V ( x , t ) так, что в минимуме правой ямы потенциал не растет, а остается постоянным далеко по оси x. Тогда точки c и d для граничных условий будут - 3 и 797 соответственно.
Для предотвращения ошибки вторичного заселения из-за отсутствия демпфирования в нашей модели [13], введем эффективное демпфирование. Так как нас интересует только туннелирование из левой потенциальной ямы, изменим V ( x , t ) так, что в минимуме правой ямы потенциал не растет, а остается постоянным далеко по оси x. Тогда точки c и d для граничных условий будут - 3 и 797 соответственно.
Для реальных систем быстрого импульсного считывания, возьмем значение длительности импульса 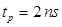 . Ясно, что эволюция волновой функции, и, следовательно, ошибка считывания N будут зависеть от формы импульса, амплитуды импульса А, постоянной компоненты поля a 0, и емкости контакта D. Наша задача состоит в разработке метода оптимизации данных параметров для увеличения надежности работы прибора. Особенностью квантовой системы является невозможность использования прямоугольного импульса, который в классической системе дает минимальную шумовую ошибку. Использование меандра приводит к возбуждению системы, переходу на более высокие уровни и туннелированию с них, что в свою очередь приводит к большой ошибке. Рассмотрим компромиссные формы импульсов.
. Ясно, что эволюция волновой функции, и, следовательно, ошибка считывания N будут зависеть от формы импульса, амплитуды импульса А, постоянной компоненты поля a 0, и емкости контакта D. Наша задача состоит в разработке метода оптимизации данных параметров для увеличения надежности работы прибора. Особенностью квантовой системы является невозможность использования прямоугольного импульса, который в классической системе дает минимальную шумовую ошибку. Использование меандра приводит к возбуждению системы, переходу на более высокие уровни и туннелированию с них, что в свою очередь приводит к большой ошибке. Рассмотрим компромиссные формы импульсов.
Параметры системы
Рассмотрим различные формы импульсов:
1. Трапецоид, изменяющийся по закону  в интервале
в интервале  (Рис. 20)
(Рис. 20)

Рис.20 Форма импульса
На Рис.21 показана зависимость N ( A ) для постоянной амплитуды смещения a 0 = 0.81 и различных значений обратной емкости D. Видно, что зависимость имеет четкий минимум по амплитуде. Это объясняется квантовой природой системы. Так же можно заметить, что, подбирая D, мы можем менять минимум Nmin ( A ). Таким образом, минимум ошибки считывания Nmin ( A , D ) ≈ 0.036 при D = 1.15; A = 0.0285. Надежность в этом случае 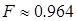 .
.

Рис.21 Ошибка считывания N в зависимости от амплитуды импульса А для различных значений D; a 0 = 0.81.
Аналогично, находим кривые с абсолютным минимумом ошибки Nmin ( A , D ) для других значений a 0 (для разных a 0 значение D, при котором достигается абсолютный минимум N, различно). На Рис.22 приведены кривые N ( A ) с минимальной ошибкой для различных a 0.

Рис.22 Оптимальные кривые N от амплитуды импульса А для различных значений D и a 0.
Таким образом, мы получили минимум N = 0.031  для параметров: a 0 = 0.77; D = 1.9; A = 0.0625. Видно, при уменьшении a 0 увеличивается значение амплитуды импульса A для тех же D. Мы можем дать рекомендацию при известных параметрах a 0 и D, где искать минимум N по А. Глубину потенциальной яме можно характеризовать количеством дискретных уровней энергии
для параметров: a 0 = 0.77; D = 1.9; A = 0.0625. Видно, при уменьшении a 0 увеличивается значение амплитуды импульса A для тех же D. Мы можем дать рекомендацию при известных параметрах a 0 и D, где искать минимум N по А. Глубину потенциальной яме можно характеризовать количеством дискретных уровней энергии  . В приближении квантового гармонического осциллятора [14]:
. В приближении квантового гармонического осциллятора [14]:
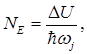 (32)
(32)
где 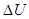 - глубина левой ямы,
- глубина левой ямы,  - частота осцилляций. Здесь x 0 - значение фазы в минимуме ямы. (зависит от формы ямы, от a 0 и A), а
- частота осцилляций. Здесь x 0 - значение фазы в минимуме ямы. (зависит от формы ямы, от a 0 и A), а  - эффективная масса (
- эффективная масса (  - квант потока). Для оптимального считывания нам необходимо, чтобы внешнее максимальное поле φ1 меняло глубину ямы до значения
- квант потока). Для оптимального считывания нам необходимо, чтобы внешнее максимальное поле φ1 меняло глубину ямы до значения  чуть большего 1. Так, для a 0 = 0.82 и D = 1.2 минимум находится в районе A = 0.0166…0.0236; а для a 0 = 0.7 и D = 2 минимум - в районе A = 0.131…0.139, что полностью подтверждается результатами численного счета.
чуть большего 1. Так, для a 0 = 0.82 и D = 1.2 минимум находится в районе A = 0.0166…0.0236; а для a 0 = 0.7 и D = 2 минимум - в районе A = 0.131…0.139, что полностью подтверждается результатами численного счета.
2. Трапецоид, изменяющийся по закону  в интервале
в интервале  (Рис.23)
(Рис.23)
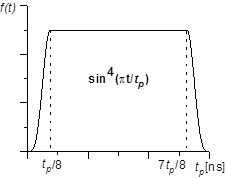
Рис.23 Форма импульса  .
.
На Рис.24 сплошной линией показана зависимость N ( A ) для разных D и a 0 = 0.81 (пунктирные линии - предыдущий импульс  для тех же параметров).
для тех же параметров).

Рис.24. Зависимость N ( A ) для разных D и a 0 = 0.81. Сплошная линия - импульс формы  . Пунктирная -
. Пунктирная - 
Как мы и предполагали, чем ближе форма импульса к прямоугольной, тем сильнее проявляется эффект осцилляций: наблюдаются несколько локальных минимумов N (для D = 1.1, N = 0.044; для D = 2.1, N = 0.045). Но по абсолютному значению, ошибка при данной форме импульса больше, чем для предыдущего случая.
3. Трапецоид, изменяющийся по закону  в интервале
в интервале  (более узкая полка по сравнению с предыдущими импульсами), Рис.25.
(более узкая полка по сравнению с предыдущими импульсами), Рис.25.

Рис.25 Форма импульса
Используя разработанный метод, находим кривые с абсолютным минимум ошибки Nmin ( A , D ) для различных значений a 0. На Рис.26 сплошной линией показана зависимость N ( A ) для импульса  . (пунктирные линии - импульс
. (пунктирные линии - импульс  с длинной полкой для тех же a 0, но своих наилучших параметров D).
с длинной полкой для тех же a 0, но своих наилучших параметров D).

Рис.26. Зависимость N ( A ) для разных D и a 0. Сплошная линия - импульс  , пунктирная -
, пунктирная - 
Так, если для  с длинной полкой минимум N = 0.031 соответствовал параметрам a 0 = 0.77; D = 1.9 То для
с длинной полкой минимум N = 0.031 соответствовал параметрам a 0 = 0.77; D = 1.9 То для  , минимум смещается в сторону уменьшения a 0 и увеличения A: N ≈ 0.034 для параметров: a 0 = 0.7; D = 3.2; A = 0.126.
, минимум смещается в сторону уменьшения a 0 и увеличения A: N ≈ 0.034 для параметров: a 0 = 0.7; D = 3.2; A = 0.126.
4. Для более широкого импульса (Рис.27) эволюция кривых N ( A ) для разных D и a 0 такая же, как и для импульса  (Рис.28), но значение ошибки Nmin ( a 0 , A , D ) больше: N ≈ 0.033 (a 0 = 0.76; D = 2.8; A = 0.065).
(Рис.28), но значение ошибки Nmin ( a 0 , A , D ) больше: N ≈ 0.033 (a 0 = 0.76; D = 2.8; A = 0.065).
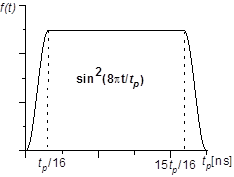
Рис.27 Форма импульса

Рис.28. Зависимость N ( A ) для разных D и a 0. Сплошная линия - импульс 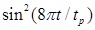 , пунктирная -
, пунктирная - 
Таким образом, удалось разработать методику поиска оптимальных параметров считывания информационного сигнала с кубита методом быстрого единичного импульса с заданной длительностью и понизить ошибку до 0.031 (то есть увеличить надежность почти до 97%).
Заключение
В работе рассматривался логический элемент квантового компьютера на основе джозефсоновских контактов. Кубит рассматривался как отдельные составляющие: сверхпроводящее кольцо, замкнутое джозефсоновским переходом и чувствительный датчик магнитного потока. Были исследованы модели СВЧ гистерезисного СКВИДа и СКВИДа постоянного тока при учете тепловых флуктуаций. Численно получены основные зависимости СКВИДов, построены графики вольт-амперной и вольт-полевой характеристик. Изучено влияние флуктуаций на выходные характеристики приборов. В частности, построены графики передаточной характеристики и меры выходного шума в зависимости от интенсивности флуктуаций тока на входе прибора. Из графиков видно, что в пределах малых шумов увеличение флуктуаций тока на входе линейно увеличивает шумовые характеристики на выходе прибора. На участке γ > 0.5, наблюдается резкий рост выходного шума.
Для СВЧ гистерезисного СКВИДа найдена область вольт-полевой характеристики, слабо зависящей от интенсивности шума, показано, что частота накачки 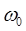 = 0.3 приближает работу прибора к минимуму ошибки измерения магнитного потока. Данные выводы хорошо согласуются с результатами других авторов. Следует отметить, что использованный нами подход для улучшения характеристик СВЧ гистерезисного СКВИДа является более универсальным так как легко может быть проверен на практике.
= 0.3 приближает работу прибора к минимуму ошибки измерения магнитного потока. Данные выводы хорошо согласуются с результатами других авторов. Следует отметить, что использованный нами подход для улучшения характеристик СВЧ гистерезисного СКВИДа является более универсальным так как легко может быть проверен на практике.
Изучен режим считывания информационного сигнала с кубита методом быстрого одиночного импульсного считывания в модели с учетом ошибки туннелирования и введенным эффективным демпфированием. Получен алгоритм выбора параметров системы для заданной длительности импульса. В частности, для импульса 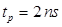 удалось понизить ошибку до 0.031 (то есть увеличить надежность считывания почти до 97%).
удалось понизить ошибку до 0.031 (то есть увеличить надежность считывания почти до 97%).
Все результаты работы в целом позволяют снизить влияние шумов на работу прибора и могут быть использованы для реальных экспериментов по измерению и считыванию сигналов с квантовых битов.
Список литературы
1. Гольцман Г.Н. Эффекты Джозефсона в сверхпроводниках. - Соросовский образовательный журнал, т.6., №4, 2000, стр.96-102.
2. Лихарев К.К. Введение в динамику джозефсоновских переходов - Москва: Наука, 1985.
3. Ustinov A. V. High-contrast readout of superconducting qubits beyond the single-shot resolution limit // Applied physics letters 2000. V.15. P.218-314
4. Castellano M. G. et. al. Magnetic field dependence of thermal excitation in Josephson junctions // IEEE Transactions on applied superconductivity. 1997. V.7. P.2430-2433.
5. Voss R. F. Macroscopic quantum tunneling in 1 - μm Nb Josephson Junctions // Physical Review Letters 1991. V.47, 265-268.
6. Barone, A. Physics and Applications of the Josepson Effect // New York: Wiley, 1982. - p.551.
7. Pankratov A. L. Optimal pump frequency for ac hysteretic SQUID // Physical Review 2003. V.68, 024503-024507.
8. Braginski A.I. Progress in understanding of high-transition temperature SQUIDs. Physica 2000. V.4. P.341-348.
9. Mannela R. Integration of stochastic differential equations on a computer // Applied physics letters 1988. V.5. P.218-232.
10. Koelle D. High-transition-temperature SQUIDs - TRW // Electronics & Technology Division. 1999. V.71. P.631-686.
11. Pankratov A. L., Gavrilov A. S. Optimal fast single-pulse readout of qubits. // Physical Review B. 2010. V.81. P.052501-1-4.
12. Press W. Numerical Recipes in C. // Cambridge University 2002.
13. Kofman G. Theoretical analysis of measurement crosstalk for coupled Josephson phase qubits. // Physical Review B. 2007. V.7. P.524--541
14. Kofman G. Analysis of measurement errors for a superconducting phase qubit. // Physical Review B. 2006. V.4. P.214518-1-214518-14.
|
из
5.00
|
Обсуждение в статье: Модель фазового кубита |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

