 |
Главная |
Нормированные пространства
|
из
5.00
|
Содержание
Введение........................................................................................................... 3
§1. Основные понятия и определения............................................................. 4
1.1. Линейные пространства........................................................................... 4
1.2. Нормированные пространства................................................................ 5
1.3. Банаховы пространства............................................................................ 6
1.4. Компактные множества............................................................................ 8
1.5. Линейные операторы и линейные функционалы.................................. 11
1.6. Сопряженные операторы....................................................................... 12
§2. Компактные операторы........................................................................... 13
2.1. Определение компактного оператора................................................... 13
2.2. Свойства компактных операторов......................................................... 13
2.3. Примеры некомпактного и компактных операторов........................... 16
Литература..................................................................................................... 20
Введение
Изучение произвольных линейных операторов представляет собой весьма трудоемкую задачу, однако среди линейных операторов можно выделить классы операторов, которые могут быть рассмотрены более подробно. Данная работа рассматривает основные понятия, свойства, определения и теоремы, связанные с одним из классов линейных операторов – компактными операторами.
Работа состоит из двух параграфов. Первый из них содержит предварительные сведения, необходимые для рассмотрения темы: понятия пространств, которые необходимы при изучении компактных операторов, понятия линейного оператора и линейного функционала, сопряженного оператора, компактного множества. Во втором параграфе рассмотрено определение компактного оператора, основные свойства этого класса операторов и примеры компактных и некомпактного оператора.
Основные понятия и определения.
Линейные пространства.
Определение: Непустое множество  элементов называется линейным, если оно удовлетворяет таким условиям:
элементов называется линейным, если оно удовлетворяет таким условиям:
I.  Для любых двух элементов
Для любых двух элементов  определен единственный элемент
определен единственный элемент  , называемый суммой и обозначаемый
, называемый суммой и обозначаемый  , причем
, причем
1)  ;
;
2)  ;
;
3) в  существует такой элемент 0, что
существует такой элемент 0, что  для всех
для всех 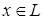 ;
;
4) для каждого 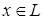 существует такой элемент
существует такой элемент  , что
, что  .
.
II. Для любого числа  и любого элемента
и любого элемента 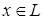 определен элемент
определен элемент  , причем
, причем
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
([1], стр. 120).
Примеры линейных пространств
1. Пространство действительных чисел  является линейным пространством по операциям сложения и умножения.
является линейным пространством по операциям сложения и умножения.
2.  – пространство, элементами которого являются последовательности чисел
– пространство, элементами которого являются последовательности чисел  , удовлетворяющих условию
, удовлетворяющих условию  с операциями
с операциями  ,
, 
([1], стр. 121).
Нормированные пространства
Определение: Множество  называется нормированным пространством, если:
называется нормированным пространством, если:
1)  – линейное пространство над полем действительных или комплексных чисел.
– линейное пространство над полем действительных или комплексных чисел.
2) Для каждого элемента 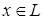 определено вещественное число, называемое его нормой и обозначаемое
определено вещественное число, называемое его нормой и обозначаемое  , и выполнены условия:
, и выполнены условия:
а)  для любого
для любого 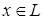 ;
; 
б)  для любого
для любого 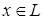 и любого
и любого  ;
;
в) 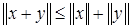 , для любых
, для любых 
([1], стр. 138).
Примеры нормированных пространств:
1. Пространство  становится нормированным, если положить
становится нормированным, если положить  .
.
2. Пространство  с элементами
с элементами  нормировано, при условии
нормировано, при условии  .
.
3. Пространство  функций, непрерывных на отрезке
функций, непрерывных на отрезке  , нормировано, если взять
, нормировано, если взять  .
.
([1], стр. 139).
Банаховы пространства
Определение: Расстоянием (метрикой) между двумя элементами 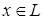 и
и 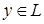 называется вещественное неотрицательное число, обозначаемое
называется вещественное неотрицательное число, обозначаемое  и подчиненное трем аксиомам:
и подчиненное трем аксиомам:
1)  ;
;
2)  ;
;
3) 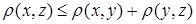 ;
;
Определение: Последовательность 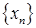 точек метрического пространства
точек метрического пространства  называется фундаментальной, если
называется фундаментальной, если  при
при  .
.
Справедливы утверждения:
1. Если последовательность  сходится к некоторому пределу, то она фундаментальна.
сходится к некоторому пределу, то она фундаментальна.
Доказательство:
Пусть  , тогда
, тогда  , при
, при 
2. Всякая фундаментальная последовательность  ограничена.
ограничена.
Определим расстояние в нормированном пространстве  , полагая для любых
, полагая для любых  . Тогда
. Тогда  означает, что
означает, что  . Это сходимость по норме.
. Это сходимость по норме.
Фундаментальная последовательность  в нормированном пространстве в соответствии с определением расстояния характеризуется условием
в нормированном пространстве в соответствии с определением расстояния характеризуется условием
 , при
, при 
Определение: Нормированное пространство называется полным, если всякая фундаментальная последовательность его элементов имеет предел.
Определение: Полное нормированное пространство называется банаховым пространством.
([2], стр. 137)
Компактные множества
Определение: Множество  в метрическом пространстве
в метрическом пространстве  называется компактным, если из всякой бесконечной последовательности
называется компактным, если из всякой бесконечной последовательности  можно выделить подпоследовательность, сходящуюся к некоторому пределу
можно выделить подпоследовательность, сходящуюся к некоторому пределу  .
.
Определение: Множество  , лежащее в некотором метрическом пространстве
, лежащее в некотором метрическом пространстве  , называется предкомпактным, или относительно компактным (компактным относительно
, называется предкомпактным, или относительно компактным (компактным относительно  ), если его замыкание в
), если его замыкание в  компактно.
компактно.
Определение: Множество  называется ограниченным, если оно содержится в некотором шаре с центром в точке
называется ограниченным, если оно содержится в некотором шаре с центром в точке  , то есть существует такая постоянная
, то есть существует такая постоянная 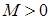 , такая, что для любого
, такая, что для любого 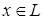 выполняется неравенство
выполняется неравенство 
В курсе теории метрических пространств доказывалось, что любое компактное множество является ограниченным. Докажем, что любое относительно компактное множество также является ограниченным.
Теорема: Множество  , лежащее в некотором метрическом пространстве
, лежащее в некотором метрическом пространстве  , и относительно компактное, является ограниченным.
, и относительно компактное, является ограниченным.
Доказательство. Замыкание множества М является компактным, следовательно, ограниченным. Но 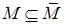 , а подмножество ограниченного множества также ограничено.
, а подмножество ограниченного множества также ограничено.
В конечномерном пространстве  выполняется также обратное утверждение.
выполняется также обратное утверждение.
Теорема: В конечномерном пространстве  всякое ограниченное подмножество относительно компактно.
всякое ограниченное подмножество относительно компактно.
Эта теорема следует из теоремы Больцано-Вейерштрасса для пространства  : в этом пространстве всякая ограниченная последовательность содержит сходящуюся подпоследовательность.
: в этом пространстве всякая ограниченная последовательность содержит сходящуюся подпоследовательность.
Можно доказать также более общую теорему.
Теорема: В конечномерном нормированном пространстве всякое ограниченное подмножество относительно компактно.
Доказательство:
Пусть  – ограниченное подмножество n–мерного пространства
– ограниченное подмножество n–мерного пространства  , т. е. существует такая константа
, т. е. существует такая константа  , что
, что  для всех
для всех  . Каждому
. Каждому  сопоставляем вектор
сопоставляем вектор  , координаты которого
, координаты которого  равны соответствующим координатам в разложении элемента
равны соответствующим координатам в разложении элемента  по некоторому фиксированному базису. Тогда справедливо следующее неравенство:
по некоторому фиксированному базису. Тогда справедливо следующее неравенство: 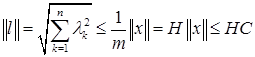 (1), где
(1), где  – наименьшее значение
– наименьшее значение  на единичном шаре
на единичном шаре  ,
,  . Возьмем любую последовательность
. Возьмем любую последовательность 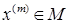 . По неравенству (1) соответствующие этим элементам векторы
. По неравенству (1) соответствующие этим элементам векторы  образуют ограниченное множество, а в
образуют ограниченное множество, а в  ограниченные множества относительно компактны, следовательно, из последовательности
ограниченные множества относительно компактны, следовательно, из последовательности  , можно выделить частичную
, можно выделить частичную  , сходящуюся к некоторому пределу.
, сходящуюся к некоторому пределу.
Сходимость в  есть сходимость по координатам, следовательно, и последовательность
есть сходимость по координатам, следовательно, и последовательность  сходится по координатам. Но тогда эта последовательность сходится к некоторому пределу и по норме (в силу непрерывности суммы и произведения в нормированных пространствах). Тем самым относительная компактность
сходится по координатам. Но тогда эта последовательность сходится к некоторому пределу и по норме (в силу непрерывности суммы и произведения в нормированных пространствах). Тем самым относительная компактность  доказана.
доказана.
Определение: Семейство  функций называется равностепенно непрерывным, если для любого
функций называется равностепенно непрерывным, если для любого  найдется такое
найдется такое  , что
, что  , для любой функции
, для любой функции  , для любых
, для любых  , таких, что
, таких, что  .
.
Определение: Семейство  функций
функций  , определенных на некотором отрезке, называется равномерно ограниченным, если существует такое число
, определенных на некотором отрезке, называется равномерно ограниченным, если существует такое число  , что
, что  , для любого
, для любого 
Теорема Арцела: Для того чтобы семейство  непрерывных функций, определенных на отрезке
непрерывных функций, определенных на отрезке  , было предкомпактно в
, было предкомпактно в  , необходимо и достаточно, чтобы это семейство было равномерно ограничено и равностепенно непрерывно.
, необходимо и достаточно, чтобы это семейство было равномерно ограничено и равностепенно непрерывно.
Теорема: Образом компактного множества при непрерывном отображении является компактное множество.
Докажем аналогичную теорему для относительно компактных множеств.
Теорема: Образом относительно компактного множества при непрерывном отображении является относительно компактное множество.
Доказательство. Пусть  – непрерывное отображение,
– непрерывное отображение,  – относительно компактное множество. Рассмотрим последовательность точек из множества
– относительно компактное множество. Рассмотрим последовательность точек из множества  :
:  ,
,  . Так как множество
. Так как множество  относительно компактно, то существует подпоследовательность
относительно компактно, то существует подпоследовательность 
 . Так как отображение
. Так как отображение 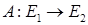 – непрерывное, то
– непрерывное, то 
 . Значит, для множества
. Значит, для множества  выполнено условие относительной компактности.
выполнено условие относительной компактности.
|
из
5.00
|
Обсуждение в статье: Нормированные пространства |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

