 |
Главная |
Свойства компактных операторов
|
из
5.00
|
1. Из определения компактного оператора и ограниченности относительно компактного множества следует, что любой линейный компактной оператор является ограниченным, следовательно, непрерывным.
2. Если  – компактный оператор,
– компактный оператор,  – ограниченный, то операторы
– ограниченный, то операторы  и
и  – компактные.
– компактные.
Доказательство. Если множество  ограничено, то множество
ограничено, то множество  тоже ограничено. Следовательно, множество
тоже ограничено. Следовательно, множество  относительно компактно, а это и означает, что оператор
относительно компактно, а это и означает, что оператор  вполне непрерывен. Далее, если
вполне непрерывен. Далее, если  ограничено, то
ограничено, то  относительно компактно, а тогда в силу непрерывности
относительно компактно, а тогда в силу непрерывности  множество
множество  тоже относительно компактно, то есть оператор
тоже относительно компактно, то есть оператор  вполне непрерывен. Теорема доказана.
вполне непрерывен. Теорема доказана.
([1], стр.241).
3. Если операторы  и
и  компактные, действующие из нормированного пространства
компактные, действующие из нормированного пространства  в нормированное пространство
в нормированное пространство  и
и  – любые числа, то оператор
– любые числа, то оператор  также компактен.
также компактен.
Доказательство. Пусть множество  ограничено. В его образе
ограничено. В его образе 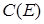 возьмем произвольную последовательность элементов
возьмем произвольную последовательность элементов  . Тогда существуют
. Тогда существуют  , при которых
, при которых  . Положим
. Положим  . При этом
. При этом  . Так как множество
. Так как множество  компактно, а
компактно, а  , то существует подпоследовательность
, то существует подпоследовательность  , имеющая предел. Аналогично в компактном множестве
, имеющая предел. Аналогично в компактном множестве  из последовательности
из последовательности 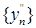 можно выделить подпоследовательность
можно выделить подпоследовательность  , имеющую предел. Но так как вместе с
, имеющую предел. Но так как вместе с  сходится и последовательность
сходится и последовательность  , то существует
, то существует  , что и доказывает компактность множества
, что и доказывает компактность множества 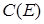 , а, следовательно, оператор
, а, следовательно, оператор  компактен. ([2], стр.306).
компактен. ([2], стр.306).
4. Если 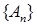 – последовательность компактных операторов в банаховом пространстве
– последовательность компактных операторов в банаховом пространстве  , сходящаяся по норме к некоторому оператору
, сходящаяся по норме к некоторому оператору  , то оператор
, то оператор  тоже компактен.
тоже компактен.
Доказательство. Для установления компактности оператора  достаточно показать, что, какова бы ни была ограниченная последовательность
достаточно показать, что, какова бы ни была ограниченная последовательность 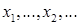 элементов из
элементов из  , из последовательности
, из последовательности  можно выделить сходящуюся подпоследовательность.
можно выделить сходящуюся подпоследовательность.
Так как оператор  компактен, то из последовательности.
компактен, то из последовательности. 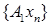 можно выбрать сходящуюся подпоследовательность. Пусть
можно выбрать сходящуюся подпоследовательность. Пусть 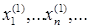 (2) – такая подпоследовательность, что
(2) – такая подпоследовательность, что  сходится.
сходится.
Рассмотрим теперь последовательность  . Из неё тоже можно выбрать сходящуюся подпоследовательность. Пусть
. Из неё тоже можно выбрать сходящуюся подпоследовательность. Пусть  такая подпоследовательность выбранная из (2), что
такая подпоследовательность выбранная из (2), что  сходится. При этом, очевидно, что
сходится. При этом, очевидно, что  тоже сходится. Рассуждая аналогично, выберем из последовательности
тоже сходится. Рассуждая аналогично, выберем из последовательности  такую подпоследовательность
такую подпоследовательность  , что
, что 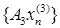 сходится и т.д. Затем возьмем диагональную последовательность
сходится и т.д. Затем возьмем диагональную последовательность  . Каждый из операторов
. Каждый из операторов  переводит её в сходящуюся. Покажем, что и оператор
переводит её в сходящуюся. Покажем, что и оператор  тоже переводит её в сходящуюся. Тем самым мы покажем, что
тоже переводит её в сходящуюся. Тем самым мы покажем, что  компактен. Так как пространство
компактен. Так как пространство  полно, то достаточно показать, что
полно, то достаточно показать, что  – фундаментальная последовательность. Имеем
– фундаментальная последовательность. Имеем
 .
.
Пусть  , выберем сначала
, выберем сначала  так, что
так, что 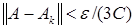 , а потом выберем такое
, а потом выберем такое  , чтобы при всех
, чтобы при всех 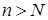 и
и  выполнялось неравенство
выполнялось неравенство  (это возможно, так как последовательность
(это возможно, так как последовательность  сходится). При этих условиях из предпоследнего неравенства получаем, что
сходится). При этих условиях из предпоследнего неравенства получаем, что  для всех достаточно больших
для всех достаточно больших 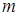 и
и  . Таким образом свойство доказано. ([1], стр. 239).
. Таким образом свойство доказано. ([1], стр. 239).
5. Оператор, сопряженный компактному оператору, компактен ([1], стр.241).
|
из
5.00
|
Обсуждение в статье: Свойства компактных операторов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

