 |
Главная |
Понятие о геодезическом и астрономическом азимутах
|
из
5.00
|
Астрономическим азимутом  направления МK называют угол между северным направлением астрономического меридиана точки наблюдения М и наблюденным направлением МK.
направления МK называют угол между северным направлением астрономического меридиана точки наблюдения М и наблюденным направлением МK.
Астрономические широты, долготы и азимуты на земной поверхности могут быть определены из наблюдений звезд.
Геодезическим азимутом А направления МK (рис.2.1)(на земной поверхности) или mk (на эллипсоиде) называют угол между северным направлением геодезического меридиана РmР' точки наблюдения и направлением МK, отредуцированным на поверхность эллипсоида. Геодезический азимут отсчитывают по ходу часовой стрелки от северного направления меридиана, от 00 до 3600.
Геодезический азимут  может быть получен двумя путями:
может быть получен двумя путями:
1) путем передачи азимутов по сторонам геодезической сети, пользуясь исходным азимутом в начальной ее точке, полученным при ориентировании референц-эллипсоида, и углами сети;
2) путем определения астрономического азимута  и получения затем геодезического азимута
и получения затем геодезического азимута  направления MK по формуле
направления MK по формуле
 , (2.1)
, (2.1)
где 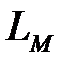 — геодезическая и
— геодезическая и  — астрономическая долготы точки М;
— астрономическая долготы точки М;  — астрономическая широта точки М ;
— астрономическая широта точки М ;  и
и  — редукционные поправки в направление MK за перенос его с земной поверхности на поверхность референц—эллипсоида, причем
— редукционные поправки в направление MK за перенос его с земной поверхности на поверхность референц—эллипсоида, причем  — поправка за уклонение отвесной линии от нормали к эллипсоиду в точке M, а
— поправка за уклонение отвесной линии от нормали к эллипсоиду в точке M, а  — поправка за высоту визирной цели в точке K над поверхностью эллипсоида. Формулы для вычисления этих малых поправок, учитываемых при высокоточных измерениях, будут даны в лекции, посвященной математической обработке результатов угловых наблюдений.
— поправка за высоту визирной цели в точке K над поверхностью эллипсоида. Формулы для вычисления этих малых поправок, учитываемых при высокоточных измерениях, будут даны в лекции, посвященной математической обработке результатов угловых наблюдений.
Геодезический азимут, полученный по формуле (2.1), называют азимутом Лапласа. Геодезический пункт, на котором были определены астрономический азимут и долгота, называют пунктом Лапласа, а поправочный член  — поправкой Лапласа.
— поправкой Лапласа.
| Z |
| У |
| Х |
| Е′ |
| Е |
| Р′ |
| Р |
| Е0 |
| О |
| 90º |
| K |
 ,
,  не совпадают между собой вследствие несовпадения в каждой точке Земли направлений нормали и отвесной линии. Сопоставление астрономических и геодезических координат позволяет вычислить астрономо - геодезические уклонения отвесных линий, т.е. угол между нормалью к эллипсоиду и отвесной линией в данной точке.
не совпадают между собой вследствие несовпадения в каждой точке Земли направлений нормали и отвесной линии. Сопоставление астрономических и геодезических координат позволяет вычислить астрономо - геодезические уклонения отвесных линий, т.е. угол между нормалью к эллипсоиду и отвесной линией в данной точке.
Система прямоугольных пространственных координат (OXYZ)отнесена к центру О земного эллипсоида (рис. 2.3).
Рис. 2.3. Система прямоугольных пространственных координат ОХУZ.
Е0 — точка пересечения Гринвичского меридиана с земным экватором.
Ось OZ располагается на полярной оси эллипсоида  ; ось ОХ — в плоскости экватора и начального (Гринвичского) меридиана РЕ0
; ось ОХ — в плоскости экватора и начального (Гринвичского) меридиана РЕ0  ;
;
ось ОУ — в плоскости экватора, но в меридиане РK  , плоскость которого составляет с плоскостью Гринвичского меридиана угол в
, плоскость которого составляет с плоскостью Гринвичского меридиана угол в  .
.
Данная система координат приобретает все большее значение в геодезии в связи с широким внедрением в практику геодезических работ так называемых спутниковых измерений.
Система плоских прямоугольных координат (х, y).
В странах бывшего Союза общегосударственная система координат принята в проекции Гаусса – Крюгера,которая получается путем проецирования точек земной поверхности на боковую поверхность цилиндра и развертывании ее в плоскость. Такой метод дал возможность разделить всю поверхность Земли на равновеликие по площади участки, ограниченные меридианами и имеющие протяжение по широте от Северного полюса до Южного (рис.2.4).
| у |


Зоны 1 2 3 4 5 6 7
Рис. 2.4. Изображение координатных зон на плоскости в проекции Гаусса-Крюгера
Под плоскими прямоугольными координатами Гаусса понимают систему прямоугольных координат, в которой за начало координат в 6- или 3 - градусной зонах принята точка пересечения дуги осевого меридиана зоны с дугой экватора. За ось абсцисс x принято изображение дуги осевого меридиана, за ось ординат y - дуги экватора (рис.2.5). Слева от условной записи ординат подписывается номер зоны.
| Экватор |
| у |
| х |
 Рис.2.5. Система плоских прямоугольных координат в проекции Гаусса
Рис.2.5. Система плоских прямоугольных координат в проекции Гаусса|
из
5.00
|
Обсуждение в статье: Понятие о геодезическом и астрономическом азимутах |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

